(此位老兄的讲解深得我意,特来推荐:http://blog.csdn.net/insistgogo/article/details/8579597)
有N件物品和一个容量为V的背包。第i件物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
POINT:
1·每种物品仅有一件,可以选择放或不放。
2·子问题---将前i件物品放入容量为V的背包中。价值总和为f[i][V];
若只考虑第i件物品的策略(放或不放),那么就可以转化为一个只牵扯前i-1件物品的问题。
①第i件放:---将前i-1件物品放入容量为V-c[i]的背包中。此时价值总和为f[i-1][V-c[i]]+w[i];
②第i件不放:---将前i-1件物品放入容量为V的背包中。此时价值总和为f[i-1][V];
即可得出状态转移方程: f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}。(重要!!!)
代码如下(http://blog.csdn.net/insistgogo/article/details/8579597)

1 #include <iostream> 2 using namespace std; 3 4 const int N = 3;//物品个数 5 const int V = 5;//背包最大容量 6 int weight[N + 1] = {0,3,2,2};//物品重量 7 int value[N + 1] = {0,5,10,20};//物品价值 8 9 int f[N + 1][V + 1]; 10 11 /* 12 目标:在不超过背包容量的情况下,最多能获得多少价值 13 14 子问题状态:f[i][j]:表示前i件物品放入容量为j的背包得到的最大价值 15 16 状态转移方程:f[i][j] = max{f[i - 1][j],f[i - 1][j - weight[i]] + value[i]} 17 18 初始化:f数组全设置为0 19 */ 20 int Knapsack() 21 { 22 //初始化 23 memset(f,0,sizeof(f)); 24 //递推 25 for (int i = 1;i <= N;i++) //枚举物品 26 { 27 for (int j = 0;j <= V;j++) //枚举背包容量 28 { 29 f[i][j] = f[i - 1][j]; 30 if (j >= weight[i]) 31 { 32 f[i][j] = max(f[i - 1][j],f[i - 1][j - weight[i]] + value[i]); 33 } 34 } 35 } 36 return f[N][V]; 37 } 38 39 int main() 40 { 41 cout<<Knapsack()<<endl; 42 return 0; 43 }
3·时间和空间复杂度,O(V*N);
4·优化(时间复杂度基本已经不能再优化了,但空间复杂度却可以优化到O(V)):
(上面f[i][v]使用二维数组存储的,可以优化为一维数组f[v])将主循环改为:
分析:我们现在使用f[v]保存中间状态,我们想要达到的效果是,第i次循环后,f[v]中存储的是前i个物体放到容量v时的最大价值
思考
①对于f[i][v], 肯定是有一个主循环i=1..N,每次算出来二维数组f[i][0..V]的所有值。(前i件物品分放入容量为0~V的背包中最大价值总和)。那么,如果只用一个数组f[0..V],能不能保证第i次循环结束后f[v]中表示的就是我们定义的状态f[i][v]呢?
②f[i][v]是由f[i-1][v]和f[i-1][v-c[i]]两个子问题递推而来,能否保证在推f[i][v]时(也即在第i次主循环中推f[v]时)能够得到f[i-1][v]和f[i-1][v -c[i]]的值呢?
---->综上,要求在每次主循环中我们以v=V..0的顺序推f[v],这样才能保证推f[v]时f[v-c[i]]保存的是状态f[i -1][v-c[i]]的值。(不懂?下面讲解)
伪代码如下:

1 for i=1..N 2 3 for v=V..0 4 5 f[v]=max{f[v],f[v-c[i]]+w[i]};
其中的f[v]=max{f[v],f[v-c[i]]+w[i]};
恰就相当于我们的转移方程f[i][v]=max{f[i-1][v],f[i- 1][v-c[i]]+w[i]},现在的f[v-c[i]]就相当于原来的f[i-1][v-c[i]]。
·我们可以看到,要想得到f[i][v], 我们需要知道 f[i-1][v]和f[i-1][v-c[i]],由于我们使用二维数组保存中间状态,所以可以直接取出这两个状态。那么一位数组呢?
当我们使用一维数组存储状态时,f[v]表示:在执行i次循环后(此时已经处理i个物品),前i个物体放到容量v时的最大价值,即之前的f[i][v]。与二维相比较,它把第一维隐去了,但是二者表达的含义还是相同的,只不过针对不同的i,f[v]一直在重复使用,所以,也会出现第i次循环可能会覆盖第i - 1次循环的结果!!
为了求f[v],我们需要知道前i-1个物品放到容量v的背包中带来的收益,即之前的f[i - 1][v]和前i-1件物品放到容量为v-c[i]的背包中带来的收益,即之前的f[i - 1][v-c[i]]+w[i]。
难点:由于我们只使用一维数组存储,则在求这两个子问题时就没有直接取出那么方便了,因为第i次循环可能会覆盖第
i-1次循环的结果。现在我们来求这两个值:
1)前i-1个物品放到容量v的背包中带来的收益,即之前的f[i-1][v]:
由于在执行在i次循环时,f[v]存储的是前i个物体放到容量v时的最大价值,在求前i个物体放到容量v时的最大价值(即之前的f[i][v])时,我们是正在执行第 i 次循环,f[v]的值还是在第i-1次循环时存下的值,在此时取出的f[v]就是前i - 1个物体放到容量v时的最大价值,即f[i - 1][v]。
2)前i-1件物品放到容量为V-c[i]的背包中带来的收益,即之前的f[i-1][V-c[i]] + w[i];
由于在执行第i次循环前,f[0 ~ V]中保存的是第i-1次循环的结果,即是前i -1个物体分别放到容量0 ~ V时的最大价值,即f[i - 1][0 ~ V]。则在执行第i次循环前,f 数组中V-c[i]的位置存储就是我们要找的前i-1件物品放到容量为V-c[i]的背包中带来的收益 (即之前的f[i - 1][V-c[i]]),这里假设物品是从数组下标1开始存储的。
逆序枚举容量的原因:
注意一点,我们是由第i-1次循环的两个状态推出第i个状态的,而且v>v-c[i],则对于第i次循环,背包容量只有当V..0循环时,才会先处理背包容量为v的状况,后处理背包容量为v-c[i]的情况。
具体来说,由于在执行v时,还没执行到v-c[i]的,因此f[v-c[i]]保存的还是第i-1次循环的结果。即在执行第i次循环 且 背包容量为v时,此时的f[v]存储的是 f[i-1][v] ,此时f[v-c[i]]存储的是f[i - 1][v-weight[i]]。
相反如果在执行第 i 次循环时,背包容量按照0..V的顺序遍历一遍,来检测第i件物品是否能放。此时在执行第i次循环且背包容量为v时,此时的f[v]存储的是 f[i - 1][v] ,但是此时f[v-c[i]]存储的是f[i][v-c[i]]。
因为,v >v-c[i],第i次循环中,执行背包容量为v时,容量为v-c[i]的背包已经计算过,即f[v -c[i]]中存储的是f[i][v - weight[i]]。即对于01背包,按照增序枚举背包容量是不对的。
总结:如果将v的循环顺序从上面的逆序改成顺序的话,那么则成了f[i][v]由f[i][v-c[i]]推知,与本题意不符,但它却是另一个重要的背包问题(完全背包)最简捷的解决方案,故学习只用一维数组解01背包问题是十分必要的。
-------------------------------我是还不明白的分割线------------------------------------------------------
增序枚举背包容量会达到什么效果?它会重复的装入某个物品,而且尽可能多的,使价值最大,当然不会不超过背包容量
而逆序枚举背包容量:背包中的物品至多装一次,使价值最大,当然不会不超过背包容量
我们首先举例说明:
逆序枚举物品
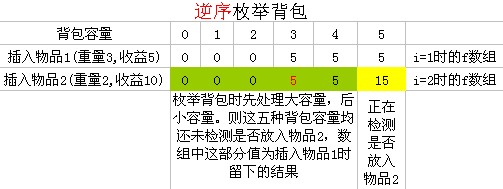
当i=2,我们要求 f[5]:表示检测物品2放入容量为5的背包的最大收益。上图表示当i=2,求f[5]时f数组的状况,绿色为数组现在存储的值,这些值是i = 1时(上一次循环)存入数组 f 的.相当于f[i - 1][v];而黄色是我们要求的值,在求f[5]之前,f[5]= 5,即f[i - 1][5] = 5;现在要求 i = 2 时的f[5]=f[5-2]+10=5+10=15>f[i - 1][5] = 5;故,f[5] = 15;
注意一点,在求f[v]时,它引用的 f[v-c[i]] 和 f[v]都是上一次循环的结果
顺序枚举物品
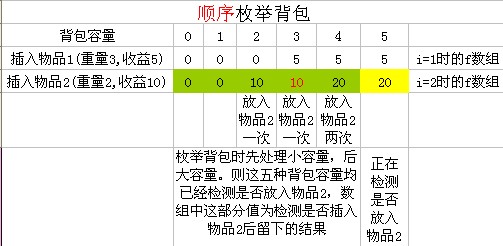
当i = 2,我们要求 f [5]:表示检测物品2放入容量为5的背包的最大收益。上图表示,当i = 2,求f[5]时f数组的状况,
绿色为数组现在存储的值,这些值是i=2时(本次循环)存入数组 f 的。相当于f[i][v]。这是由于我们是增序遍历数组f的,在求f[v]时,v之前的值(0~v-1)都已经在第i次循环中求出。
而黄色使我们要求的值,在求f[5]之前,f[5]= 5,即f[i - 1][5] = 5;
现在要求i=2时的f[5]=f[5 - 2] + 10 =10+10=20>f[i - 1][5] = 5;故,f[5] = 20;
其中引用的f[3]是相当于f[i][3] 而不是正常的f[i - 1][3];
注意一点,在求f[v]时,它引用的 f[v-c[i]]是本次循环的结果 而f[v]是上一次循环的结果;
换个角度说,在检测背包容量为5时,看物品2是否加入;由状态转移方程可知,我们f[5]需要引用自己本身和f[3],由于背包容量为3时,可以装入物品2,且收益比之前的大,所以放入背包了。在检测f[5]时,肯定要加上物品2的收益,而f[5]在引用f[3]时,f[3]时已经加过一次物品2,因此,在枚举背包容量时,物品2会加入多次。
进一步说:我们观察一维状态转移方程:
f[i][v] = max(f[i-1][v],f[i-1][v-c[i]]+w[i])
首先我们明确三个问题
1) v-c[i] < v
2) 状态f[i][v] 是由 f[i-1][v] 和 f[i-1][v-c[i]] 两个状态决定;
3) 对于物品i,我们在枚举背包容量时,只要背包容量能装下物品i 且 收益比原来的大,就会成功放入物品i。
具体来说,枚举背包容量时,是以递增的顺序的话,由于v-c[i] < v,则会先计算 v-c[i]。在背包容量为v-c[i]时,一旦装入了物品i,由于求f[v]需要使用f[i-1][v-c[i]],而若求f[v]时也可以装入物品i的话,那么在背包容量为v时,容量为v的背包就装入可两次物品。又若v-c[i]是由之前的状态推出,它们也成功装入物品i的话,那么容量为v的背包就装入了多次物品i了。
注意,此时,在计算f[v]时,已经把物品i能装入的全装入容量为v的背包了,此时装入物品i的次数为最大
其实,顺序枚举容量是完全背包问题最简捷的解决方案。
初始化的细节问题
求最优解的背包问题时,有两种问法:
1)在不超过背包容量的情况下,最多能获得多少价值
2)在恰好装满背包的情况下,最多能获得多少价值
主要的区别为是否要求恰好装满背包。但这两种问法的实现方法是在初始化的时候有所不同。
1)恰好装满背包的情况:使用二维数组f[i][v]存储中间状态,其中第一维表示物品,第二维表示背包容量
初始化时,除了f[i][0] = 0(第一列)外,其他全为负无穷。
原因:初始化 f 数组就是表示:在没有任何物品可以放入背包时的合法状态。对于恰好装满背包,只有背包容量为 0(第一列),可以什么物品都不装就能装满,这种情况是合法情况,此时价值为0。其他f[0][v](第一行)是都不能装满的,此时有容量没物品。而其他位置(除去第一行和第一列的位置),我们为了在计算中比较最大值,也要初始化为负无穷。我们从程序的角度上看,我们只允许装入背包物品的序列的起始位置是从第一列开始,这些起始位置都是合法位置,且能恰好装满的情况收益均为正值,到f[N][V]终止。
注意,我们虽然是求恰好装满,还是需要枚举所有可以装入背包的物品,只要能装入,还需装入,收益有增加。只不过,由于恰好装满的物品的序列肯定是从第一列某行开始的,且之后的收益肯定是正值。对于非恰好装满的物品序列,起始位置肯定是从第一行某位置开始的,由于此时被初始化为负无穷,在和那些恰好装满物品序列带来的价值时,肯定是小的。所以,我们最后能获得最大值。

2)不需要把背包装满,只需要收益最大
使用二维数组f[i][v]存储中间状态,其中第一维表示物品,第二维表示背包容量
初始化时,除了f[i][0]=0(第一列)外,其他全为负无穷。
使用一维数组f[v]存储中间状态,维表示背包容量,如果背包并非必须被装满,那么任何容量的背包都有一个合法解“什么都不装”,这个解的价值为0,所以初始时状态的值也就全部为0了

总结
01背包问题是最基本的背包问题,它包含了背包问题中设计状态、方程的最基本思想,另外,别的类型的背包问题往往也可以转换成01背包问题求解。故一定要仔细体会上面基本思路的得出方法,状态转移方程的意义,以及最后怎样优化的空间复杂度。
完全背包优化:(待续)
①简单优化
1)将费用大于V的物品去掉;
2)若两件i, j物品满足c[i] >= c[j] && w[i] <= w[j],则可将物品i去掉不用考虑;
