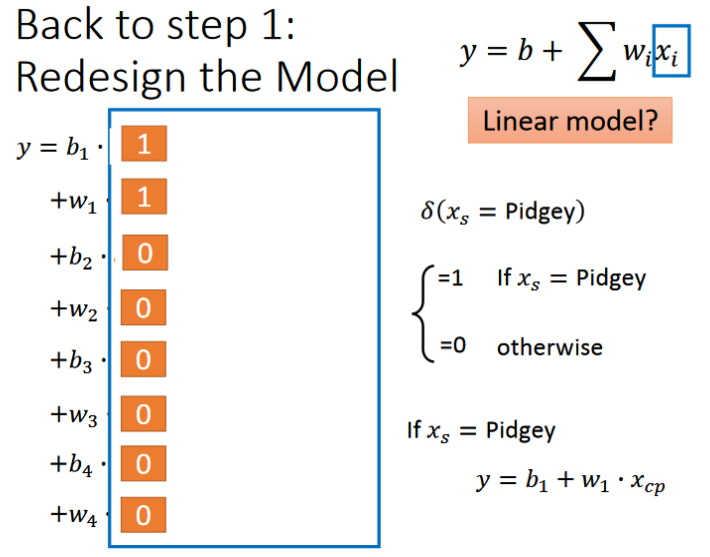
Regression
(Regression:回归

这个解释是我觉得最靠谱的解释,合理的揭示了回归的含义——用观察使得认知接近真值的过程,回归本源。
在我们认知(测量)这个世界的时候,我们并不能得到这个世界的全部信息(真值),只能得到这个世界展现出的可被我们观测的部分信息。那么,如果我们想得到世界的真值,就只能通过尽可能多的信息,从而使得我们的认识,无限接近(回归)真值。
其中,真值的概念是一个抽象的概念(感觉是从统计学中给出的)。真值是真实存在于这个世界的,但是却又永远无法真正得到。因为,无论是受限于我们自身的认知水平,还是测量手段,都会存在偏差,导致无法得到真值。就像海森堡测不准原理一样,永远不可能知道一个确定的真值。
二.回归分析(Regression analysis)
所谓回归分析,是分析自变量与因变量之间定量的因果关系,并且用回归方程描述。
结合上面所说的回归的含义,我们可以重新对回归分析进行解释。也就是,通过更多的数据(自变量和因变量),使得回归方程的参数更加准确,更能精确地描述自变量和因变量之间的关系。这里的真值是什么呢?就是自变量和因变量之间的关系。我们的认知又是什么呢?就是回归方程的参数。
而这里引入了一个新的概念——因果性。因果性关注的其实就是因和果之间的关系。那么回归分析完成的就是,让我们现有的认知无限接近因和果之间的关系。这里面的因果是一种空间上的因果,而时间上的因果可见后面的自回归(AR)。
由此,我们又可以看出,真值的表现可以通过关系的形式表现。它并不是存在那里的一个向量,而是描述向量之间的关系。就像我们的大脑一样,我们的大脑中并没有一个像电脑一样的存储介质来存储记忆。而是,通过数量众多的神经元,组成的繁杂的神经元网络中的联系(关系)来存储的。
三.其他回归
3.1线性回归(linear Regression)
以线性形式描述回归方程。
3.2自回归(Auto Regression,AR)
因变量和自变量都为同一个变量的回归方法 )
Regression-Case Study
(Regression可以做很多事情,例如Stock Market Forecast、Self-driving Car、Recommendation等等 ,在这里是通过预测宝可梦(pokemons)进化后过的CP值(战斗力),来说明Regression)
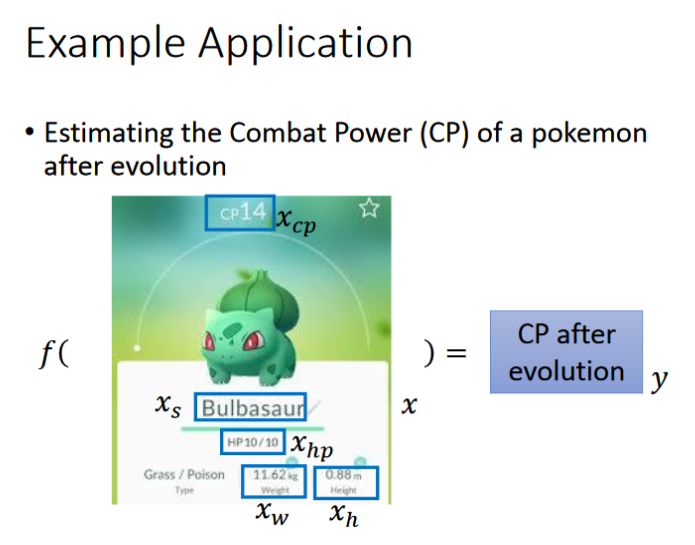
- 输入一个pokemons,通过f()函数,输出进化后的cp值

- 接下来就要寻找合适的model,首先会有一堆的function,我们假设模型为y=b+w*x(线性模型),对应的w和b可能有多种,现在需要从其中找到最好的一组

- 通过训练集寻找最好的function
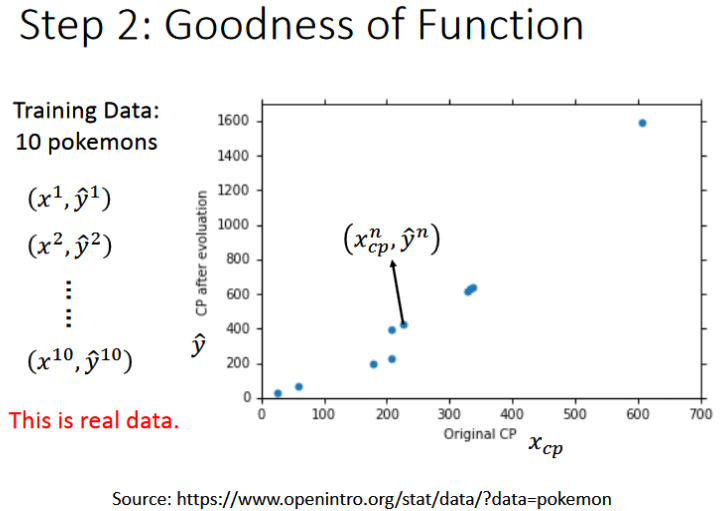
- 将训练集中的数据输入,包括x和真实的cp值,建立一个相关的坐标轴如上图,可以看出有一条大致的曲线符合函数
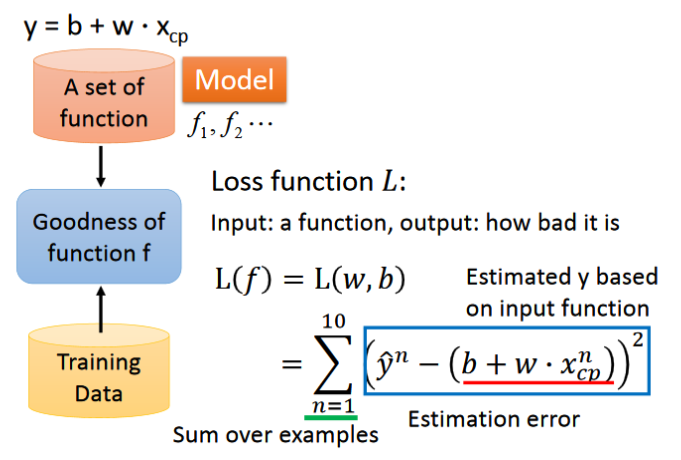
- 为了判断得到的function是否为最佳的function,引入了一个Loss function L(即函数的函数),它是通过输入一个函数,从而输出这个函数有多差,将这个函数定义为如上的形式,其中括号内的部分表示真实值和预测值差多少,整体表示估测误差的平方和。
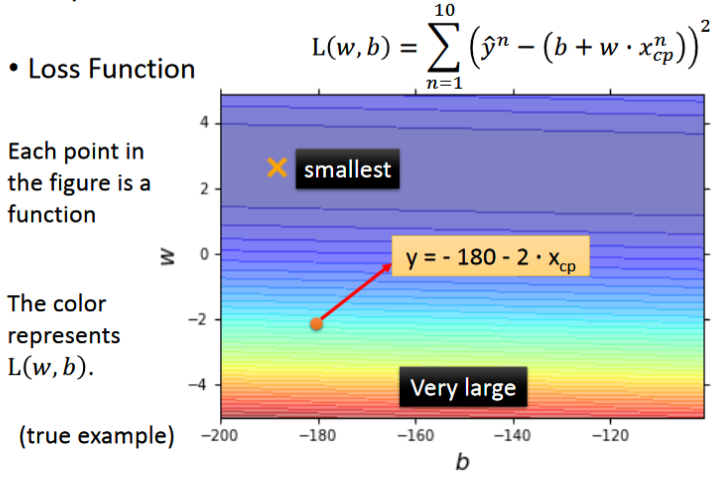
- 倘若以f的b和w分别作为横纵坐标,则图中的每一个点都将会对应一个 function,现在需要从其中选择loss最小的时候对应的w和b,其中红色部分的loss非常大,属于不好的function,蓝色部分属于较好的function
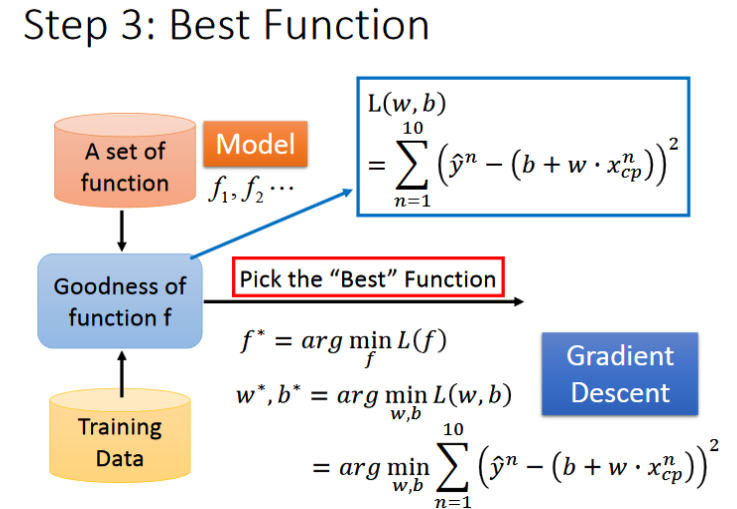
- 现在我们需要选择一个最好的function,在这里我们采用梯度下降算法来对w和b进行调整,选出的w和b要使得loss函数最小L()

- 在上图中首先只考虑一个参数即参数w,我们的目的是寻找loss最小时对应的w值为多少,即找到图中L(w)最低点
- 分为两步:(1)首先随机的选取一个w0值 (2)计算w值为w0时对应的微分值(即斜率),如果结果为正,则说明处于图像的上升部分,需要减小w的值;反之若为负,则需要增大w
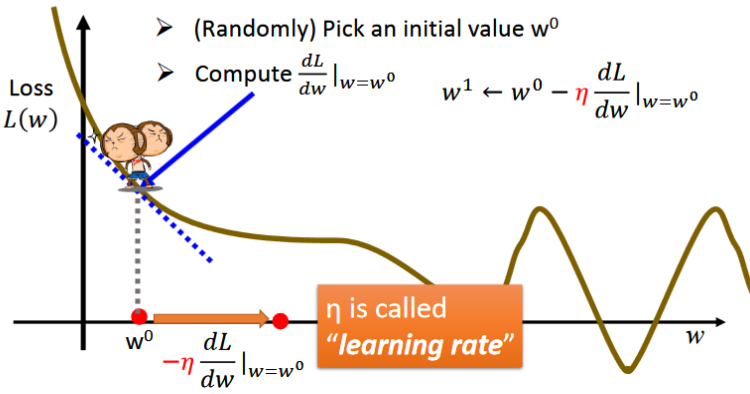
- 紧接着需要更新w的值为w1,更新的公式如上图中w1所示,按照这样的模式不断更新参数知道找到最佳的w值为止。
- gradient descent的增加量(往右踏一步的stepsize取决与两件事:1.现在的微分值有多大,越大说明在越陡峭的地方,移动距离就越大。2.常数η学习率)
- learning rate是一个事先定好的数值,若其越大,则说明踏一步参数更新的幅度就比较大,否则就比较小。越大学习的效率就比较高
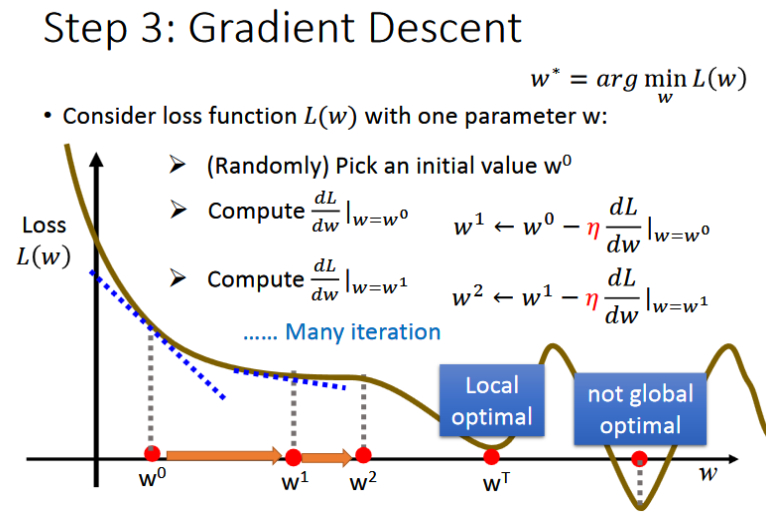
- 在这个过程中你可能会担心找到wT(local optimal局部最优),而忽略not global optimal的w值,但其实这个问题不需要担心。

- 当然,假如有两个参数呢?这里,我们假设参数为w和b,我们的目的依旧是找到loss最小时对应的w和b的值
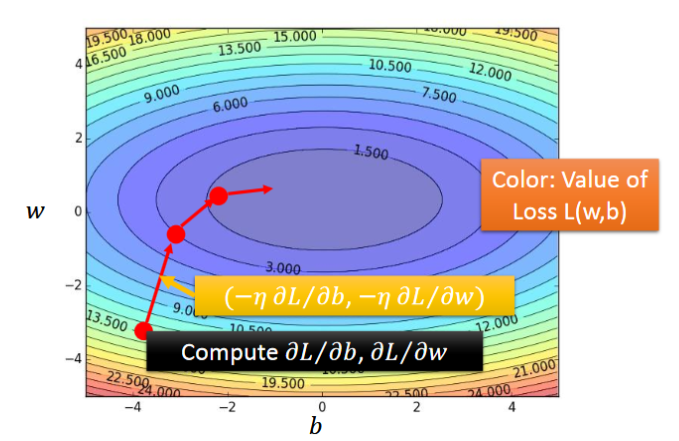
- (Randomly)首先随机选取w0值和b0值
- (Compute)分别计算对于w和b的偏导值;(更新)利用上面给定的公式更新w1,b1等(其中η为学习率,∂L/∂w或∂L/∂b 越大→越陡→w或b移动距离越大,若∂L/∂w或∂L/∂b小于0,则需要增大w和b,因此是相反的,故而用“-”)
- 按照2的方式继续更新参数
- Gradient指的是

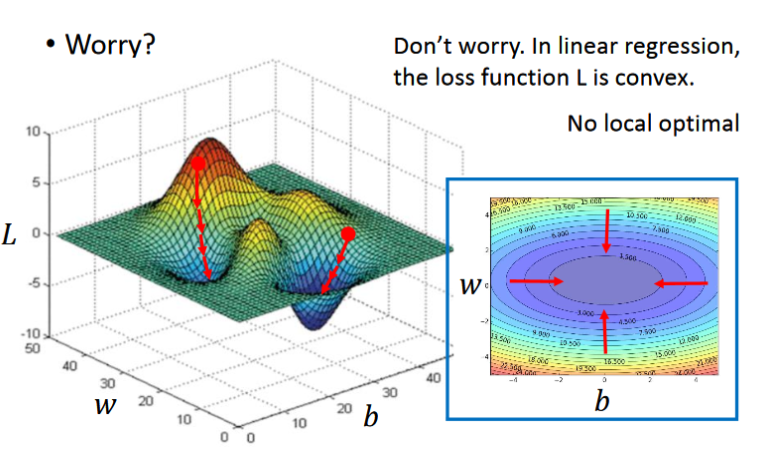
- 这其中你可能会担心的一个问题:会不会陷入局部最优的问题。在linear regression中这个问题不需要担心,因为在中loss function L 是convex的,即没有local optimal的位置的,其等高线是一圈圈的,没有local optimal的位置,随便选一个起始点,根据gradient descent选出来的都会是同一组参数
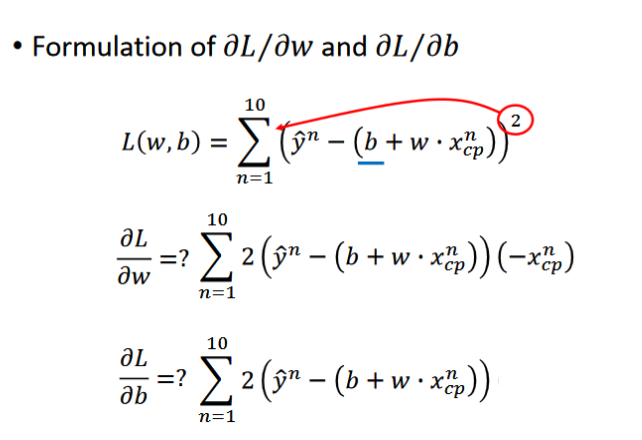
- 计算∂L/∂w或∂L/∂b
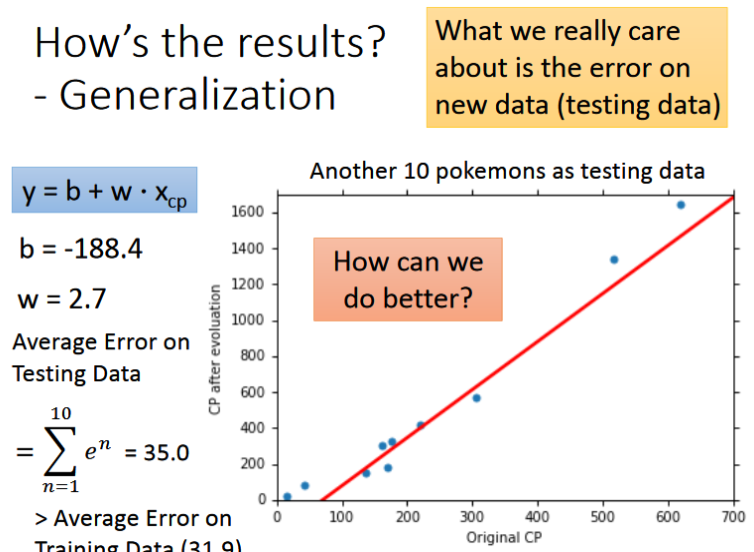
- 通过上面的一系列参数更新计算,最终得到一组w和b,确定了一个函数f,如图所示,可以看到有很多的数据并没有很好滴拟合函数,这样就可能造成预测不准确的问题,还需要对函数进行进一步的优化。

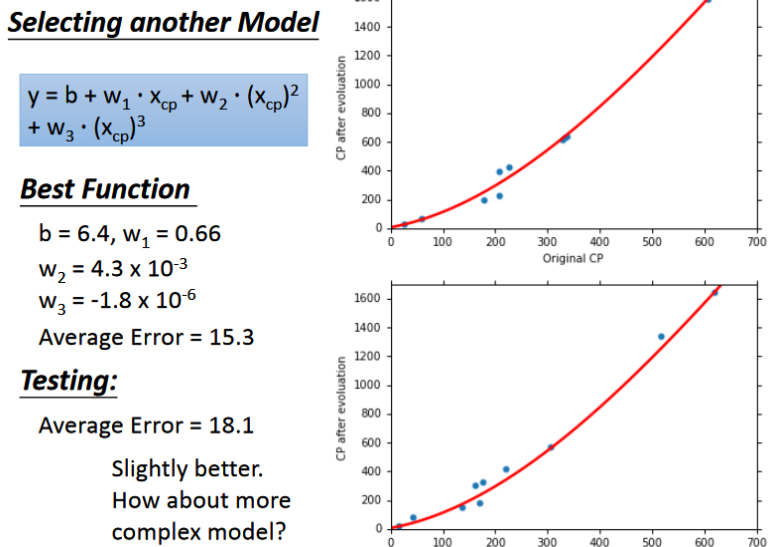


- 在上面的模型中我们采用一次方程,不难想象如果我们采用二次,三次以及多次的效果会不会更好一些。

- 然而实验证明并不一定如此。

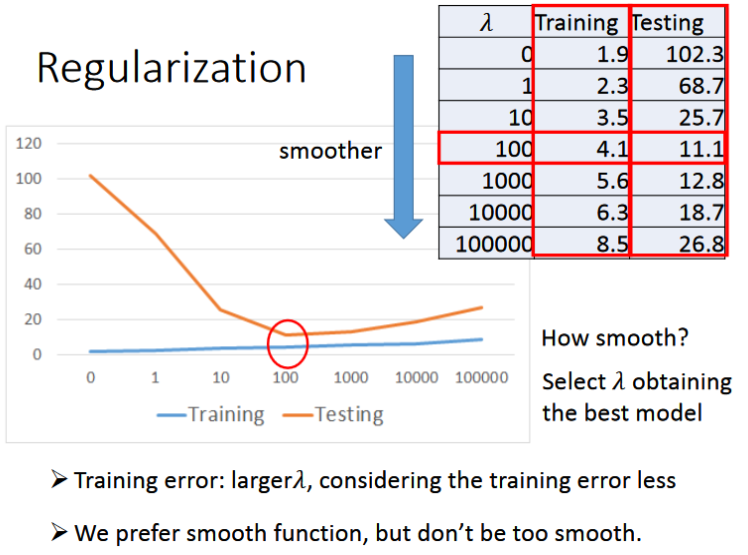
- 通过实验可以发现当我们增加函数的次数时,函数越复杂,在训练集上的error会越小即拟合地越好,然而在测试集上的效果却不一定很好,反而会变差。这种现象叫做overfitting(过拟合)
现收集更多的数据,可能包含多种不同的函数,不同的种类,现在我们回到step1重新设计函数

由此看出每一种类的x会对应一个y函数,为了方便表示,可以将其进行归纳统一