

最开始我是暴力打表的,但数据范围还是太大了,直接炸空间。
(1)20%数据:直接枚举。时间复杂度:O(nm)。
(2)另40%数据:
将式子转化一下:x≡17(mod ai)=> x mod ai =17 mod ai => (x-17) mod ai=0(注意已保证ai >17,所以17 mod ai =17),于是问题变为求0到m-17的整数中至少能被{an}中一个数整除的有多少个。
1到n的正整数中,能被x整除的数的个数Nx=n/x(“/”表示整除,下同),同时被x、y整除的数个数Nxandy=n/LCM(x,y)(LCM为最小公倍数)。根据容斥原理,|A∪B|=|A|+|B|-|A∩B|(|A|表示集合A元素个数),可得1到n的正整数中,能被x或y整除的数个数Nxory=Nx+Ny-Nxandy=n/x + n/y - n/LCM(x,y)。对于三个数x、y、z的情况,只要类比一下,画画图就可以知道,(可能你早就知道)Nxoryorz=Nx+Ny+Nz-Nxandy-Nxandz-Nyandz+Nxandyandz =n/x + n/y + n/z - n/LCM(x,y) - n/LCM(x,z) - n/LCM(y,z) + n/LCM(x,y,z)。
时间复杂度:O(logm)(辗转相除)
(3)100%数据:容斥原理是可以扩展到n个集合的——(懒得打了)
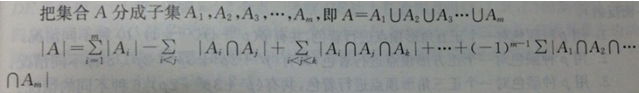
这时我们需要用个dfs枚举每个ai选与不选,若选出k个数,且k为奇数,则ans加上m/LCM(选出的数),若为偶数ans减去m/LCM(选出的数)。当然,还要加上优化,包括可行性剪枝(选出的数的LCM要小于等于m。由于ai >17,该剪枝十分有效)、优化搜索顺序(先搜大数)。时间复杂度:O(2nlogm)(实际小得多)。
其实想通了还是挺简单的,数学还应加强啊
这道题光暴力就有60分,但我却一分未得,值得反思。
#include<bits/stdc++.h> using namespace std; const int maxn=1e6+7; int a[maxn]; int n,m; long long ans; long long GCD(long long x,long long y){if(y==0) return x;else return GCD(y,x%y);} long long LCM(long long A,long long B){return A*B/GCD(A,B);} bool cmp(const int &a,const int &b){return a>b;} void dfs(long long i,long long k,long long s) { if(s>m||i==n+1) return; long long ss=LCM(a[i],s); if(k&1) ans+=m/ss;//如上图公式,选奇数个就加,反之则减 else ans-=m/ss; dfs(i+1,k+1,ss); dfs(i+1,k,s); } int main() { //freopen("c17.in","r",stdin); //freopen("c17.out","w",stdout); scanf("%d%d",&n,&m); m-=17; for(int i=1;i<=n;i++) { scanf("%d",&a[i]); } sort(a+1,a+1+n,cmp); if(m<0) { ans=0; printf("0"); return 0; } else { dfs(1,1,1); } printf("%d",ans+1); return 0; }