题目描述
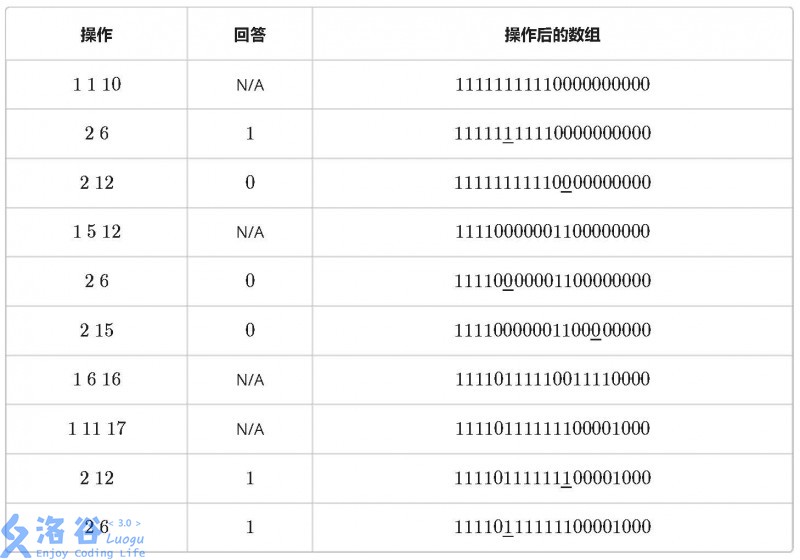
有一个 n 个元素的数组,每个元素初始均为 0。有 m 条指令,要么让其中一段连续序列数字反转——0 变 1,1 变 0(操作 1),要么询问某个元素的值(操作 2)。 例如当 n = 20 时,10 条指令如下:
输入输出格式
输入格式:
第一行包含两个整数 n, m,表示数组的长度和指令的条数; 以下 m 行,每行的第一个数 t 表示操作的种类:
若 t = 1,则接下来有两个数 L, R,表示区间 [L, R] 的每个数均反转; 若 t = 2,则接下来只有一个数 i,表示询问的下标。
输出格式:
每个操作 2 输出一行(非 0 即 1),表示每次操作 2 的回答。
输入输出样例
说明
对于 50% 的数据,1 ≤ n ≤ 10^3, 1 ≤ m ≤ 10^4; 对于 100% 的数据,1 ≤ n ≤ 10^5, 1 ≤ m ≤ 5 × 10^5,保证 L ≤ R。
线段树的区间修改,单点查询,似乎并不用建树,建树好像还有问题
#include<bits/stdc++.h> using namespace std; const int maxn=1e6+7; int xxoo[maxn]; int n,m,L,R,opt,x; void pushdown(int now) { if(xxoo[now]) { xxoo[now*2]^=1; xxoo[now*2+1]^=1; xxoo[now]=0; } } void modify(int now,int l,int r,int stdl,int stdr) { if(stdl>=l&&stdr<=r) { xxoo[now]^=1; return; } pushdown(now); int mid=(stdl+stdr)>>1; if(l<=mid) { modify(now<<1,l,r,stdl,mid); } if(r>mid) { modify(now<<1|1,l,r,mid+1,stdr); } } int query(int now,int x,int stdl,int stdr) { if(stdl==stdr) { return xxoo[now]; } pushdown(now); int mid=(stdl+stdr)>>1; if(x<=mid) { return query(now<<1,x,stdl,mid); } else { return query(now<<1|1,x,mid+1,stdr); } } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { scanf("%d",&opt); if(opt==1) { scanf("%d%d",&L,&R); modify(1,L,R,1,n); } else { scanf("%d",&x); printf("%d ",query(1,x,1,n)); } } return 0; }
错误代码(多了一个建树)
#include<bits/stdc++.h> using namespace std; const int maxn=1e6+7; struct node { int l; int r; int lazyxor; int value; int sum; }tree[maxn*4]; int n,m,L,R,opt,x; void build(int now,int l,int r) { tree[now].l=l; tree[now].r=r; tree[now].lazyxor=0; if(l==r) { tree[now].value=tree[now].sum=0; return; } int mid=(l+r)>>1; build(now<<1,l,mid); build(now<<1|1,mid+1,r); tree[now].sum=tree[now*2].sum+tree[now*2+1].sum; } void pushdown(int now) { if(tree[now].lazyxor) { tree[now*2].lazyxor^=1; tree[now*2+1].lazyxor^=1; tree[now].lazyxor=0; } } void modify(int now,int l,int r) { if(tree[now].l>=l&&tree[now].r<=r) { tree[now].lazyxor^=1; return; } pushdown(now); int mid=(tree[now].l+tree[now].r)>>1; if(l<=mid) { modify(now<<1,l,mid); } if(r>mid) { modify(now<<1|1,mid+1,r); } } int query(int now,int x,int l,int r) { if(tree[now].l==tree[now].r) { return tree[now].lazyxor; } pushdown(now); int mid=(tree[now].l+tree[now].r)>>1; if(x<=mid) { return query(now*2,x,l,r); } else { return query(now*2+1,x,l,r); } } int main() { scanf("%d%d",&n,&m); build(1,1,n); for(int i=1;i<=m;i++) { scanf("%d",&opt); if(opt==1) { scanf("%d%d",&L,&R); modify(1,L,R); } else { scanf("%d",&x); printf("%d ",query(1,x,1,n)); } } return 0; }