C++ 八数码问题宽搜
题目描述
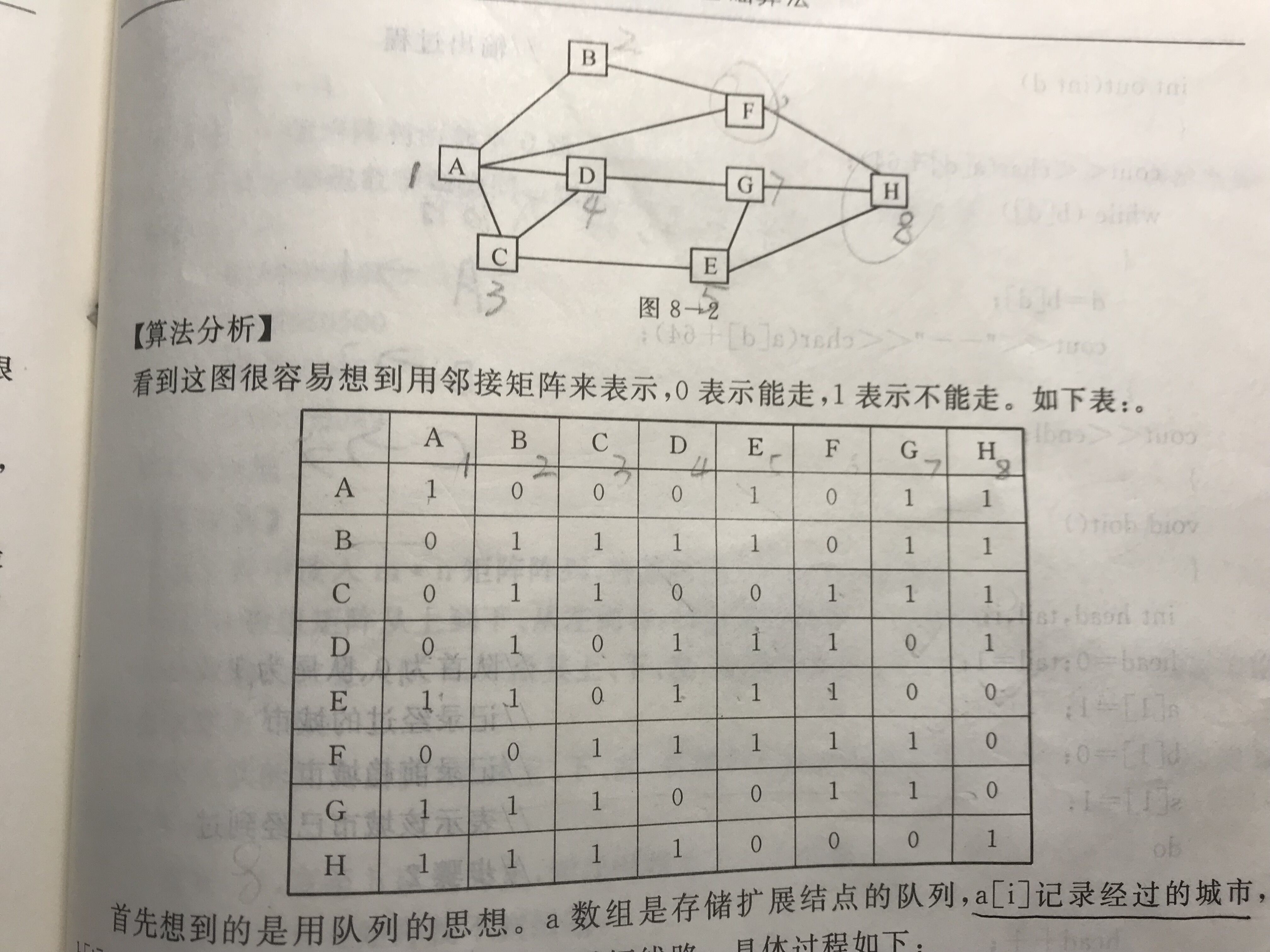
照片中表示的是从城市A到城市H的交通图。从图中可以看出,城市A到H要经过若干个城市。现在要找出一条经过城市最少的路线。
具体过程如下:
(1)讲城市A入队,队首为0,队尾为1
(2)将队首所指向的城市,所有可以直通的城市入队(如果这个城市在队列中出现过,就不入队,可以用一个布尔数组s[i]来判断),将入队城市的前趋城市保存在b[i]中,然后将队首加1,得到新的队首城市。重复以上步骤,知道搜到城市H时,搜索结束。利用b[i]可倒推出最少城市路线。
样例输入
(none)
样例输出
H--F--A
AC代码
#include <iostream>
#include <stdio.h>
#include <string.h>
using namespace std;
int ju[9][9] = {{0,0,0,0,0,0,0,0,0},
{0,1,0,0,0,1,0,1,1},
{0,0,1,1,1,1,0,1,1},
{0,0,1,1,0,0,1,1,1},
{0,0,1,0,1,1,1,0,1},
{0,1,1,0,1,1,1,0,0},
{0,0,0,1,1,1,1,1,0},
{0,1,1,1,0,0,1,1,0},
{0,1,1,1,1,0,0,0,1}};//根据图来生成矩阵
int a[101],b[101];//a是经过的城市 b是记录前趋城市
bool s[9];//true为不可走 false为可走 为了避免重复
void out(int d)//作用是把数组按char输出
{
cout << char(a[d] + 'A' - 1);//将数字转换成字母 (一个数字 +'A'-1 (+64) 才是char)
while (b[d])//重复输出,直到没有前趋城市为止(达到起点)
{
d = b[d];
cout << "--" << char(a[d] + 'A' - 1);//后面的数字用"--"隔开
}
cout << endl;
}
void doit()
{
int head,tail,i;
head = 0;tail = 1;//head出队下标 tail入队下标
a[1] = 1;//a[]是现在经过的城市 把起点的城市放在队列的第一个数
b[1] = 0;//b[]保存入队城市的前趋城市 因为A没有前趋 所以为0
s[1] = 1;//s[]判断是否能走或是否被选择过 0是能或者没被选择 1是不能或者已被选择
///////////////////////////Start to BFS/////////////////////////////////////
do//重复执行直到出队下标 <= 入队下标 保证不越界 (head < tail)
{
head ++;//head是出队下标
for (i = 1;i <= 8;i ++)//每一行遍历8列的矩阵元素
{
if (ju[a[head]][i] == 0 && s[i] == 0)//如果这个城市可以走,并且以前没有入队,那就入队
{//s[]控制入队元素是否重复
tail ++;//入队下标 + 1
a[tail] = i;//入队都入队
b[tail] = head;
s[i] = 1;//把当前城市标为已经选择过
if (i == 8)//因为目标在第8列
{
out(tail);//输出函数 递归输出目标城市的前趋城市(即为起点到目标城市的最短路线)
head = tail;//
break;//直接退出
}
}
}
}while (head < tail);
}
int main()
{
// freopen("out.txt","w",stdout);
memset(s,false,sizeof(s));//把s下标里的元素全部初始化为False
doit();//调用
return 0;//
}

