一、前述
L1正则,L2正则的出现原因是为了推广模型的泛化能力。相当于一个惩罚系数。
二、原理
L1正则:Lasso Regression
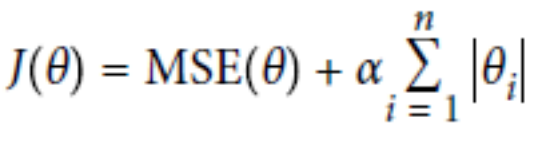
L2正则:Ridge Regression

总结:
经验值 MSE前系数为1 ,L1 , L2正则前面系数一般为0.4~0.5 更看重的是准确性。
L2正则会整体的把w变小。
L1正则会倾向于使得w要么取1,要么取0 ,稀疏矩阵 ,可以达到降维的角度。
ElasticNet函数(把L1正则和L2正则联合一起):

总结:
1.默认情况下选用L2正则。
2.如若认为少数特征有用,可以用L1正则。
3.如若认为少数特征有用,但特征数大于样本数,则选择ElasticNet函数。
代码一:L1正则
# L1正则 import numpy as np from sklearn.linear_model import Lasso from sklearn.linear_model import SGDRegressor X = 2 * np.random.rand(100, 1) y = 4 + 3 * X + np.random.randn(100, 1) lasso_reg = Lasso(alpha=0.15) lasso_reg.fit(X, y) print(lasso_reg.predict(1.5)) sgd_reg = SGDRegressor(penalty='l1') sgd_reg.fit(X, y.ravel()) print(sgd_reg.predict(1.5))
代码二:L2正则
# L2正则 import numpy as np from sklearn.linear_model import Ridge from sklearn.linear_model import SGDRegressor X = 2 * np.random.rand(100, 1) y = 4 + 3 * X + np.random.randn(100, 1) #两种方式第一种岭回归 ridge_reg = Ridge(alpha=1, solver='auto') ridge_reg.fit(X, y) print(ridge_reg.predict(1.5))#预测1.5的值 #第二种 使用随机梯度下降中L2正则 sgd_reg = SGDRegressor(penalty='l2') sgd_reg.fit(X, y.ravel()) print(sgd_reg.predict(1.5))
代码三:Elastic_Net函数
# elastic_net函数 import numpy as np from sklearn.linear_model import ElasticNet from sklearn.linear_model import SGDRegressor X = 2 * np.random.rand(100, 1) y = 4 + 3 * X + np.random.randn(100, 1) #两种方式实现Elastic_net elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5) elastic_net.fit(X, y) print(elastic_net.predict(1.5)) sgd_reg = SGDRegressor(penalty='elasticnet') sgd_reg.fit(X, y.ravel()) print(sgd_reg.predict(1.5))