【机器学习】--线性回归从初识到应用

一.前述

线性回归是机器学习的基础，所以比较重要。这里边线性是指一次，回归实际上就是拟合。Copy过来一段线性回归的描述如下：确定一个唯一的因变量（需要预测的值）和一个或多个数值型的自变量（预测变量）之间的关系。线性回归是一种有监督的机器学习，何谓有监督：实际上就是我们的数据集既要有X,又要有Y。

1、机器学习（数据挖掘的一般过程）：

定义挖掘目标
• 数据取样
• 数据探索
• 数据预处理
• 挖掘建模
• 模型评价

2、举例：

3、回归和分类的模型区别

有些Y标记是连续的，回归
有些Y标记是离散的，分类

二.原理 

先明确几个概念：

1.比如y=a+bx是我们根据样本预测出来的曲线，那么这里面的a,b这些参数就是我们的模型（Model），我们的算法（Algorithm）就是这里面的公式。

2.最大似然估计（最大可能性概率）：机器学习做的事情就是已知数据集X，Y求解拟合出来的曲线的参数w,而最大似然估计就是当w取什么值的时候代入公式中，x,y的出现概率最大。

3.大自然的一切都是回归到一定区间之内的也就是趋于平均，所以我们可以大胆假设两个条件：

   3.1 预测出来的预测值和真实值之间的误差足够多的情况下的叠加的分布符合均值u为0，方差为某定值的正态分布。

   3.2 所有样本独立分布。

相 关系数
• 两个变量之间的相关系数是一个数，它表示两个变量服从一条直线的关系有多麽紧密。
• 相关系数就是指Pearson相关系数，它是数学家Pearson提出来的，相关系数的范围是-1~+1之间，两端的值表示一个完美
的线性关系。
• 相关系数接近于0则表示不存在线性关系。协方差函数cov()，标准方差函数sd()，可以求出来cor()。

 误差的概率密度函数：

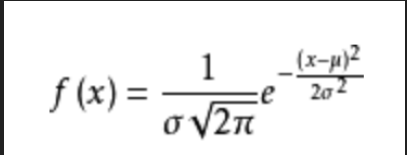
误差函数：

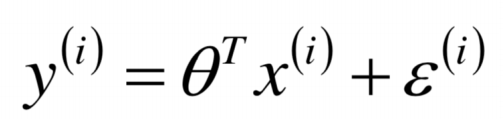
把误差带进来：

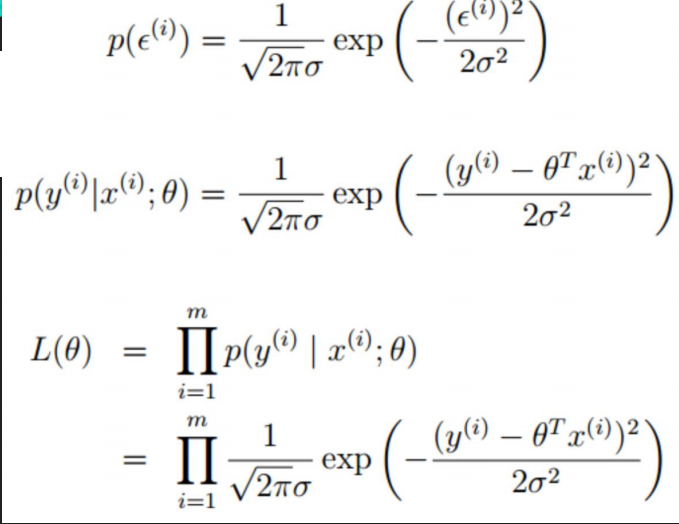
 ps:以上最后求出最大似然估计，因为每个样本点是相互独立的，所以似然函数求最大，即为每个样本点相乘。

上式中取Log函数即：

要使上面似然函数最大，也就是让最后的误差函数最小！！！！

所以有两种办法：

第一种解析解：

根据数学中函数对上式求导后求解可得。

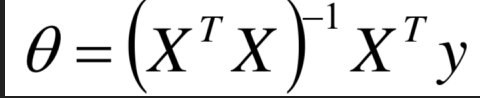
第二种最小梯度下降法：

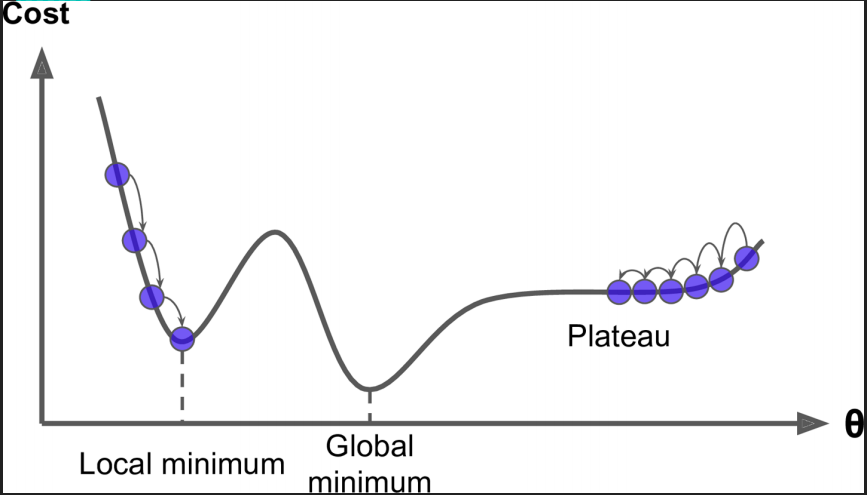
梯度下降的核心是以最快的速度找到最优解 。我们的目的就是找到损失函数的一组w参数值，所以结合图像可知线性回归的图像是一个凸函数，也就是损失函数求导为0，也就是最低端与损失函数相切的那一组w参数。

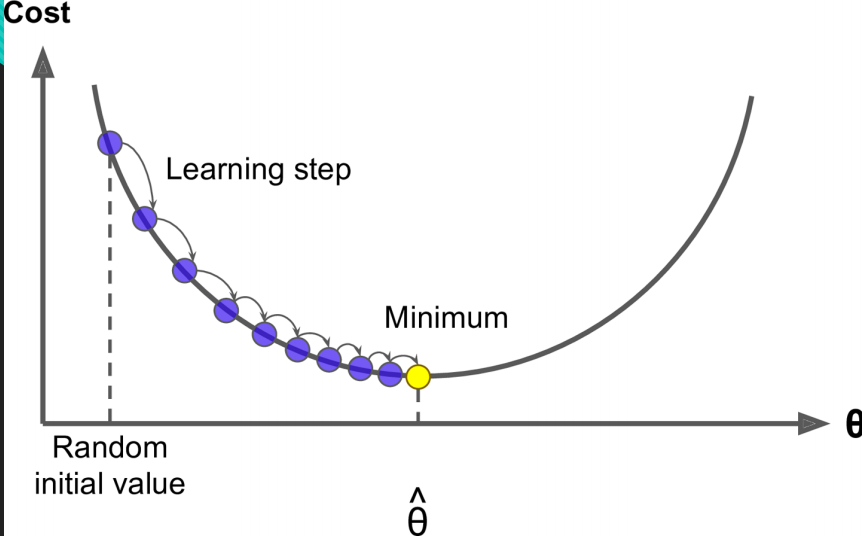
因为我们最终是要使损失函数减小，所以我们沿着损失函数的切线走会下降的最快：

我们有如下公式使每一次的损失函数都减小：

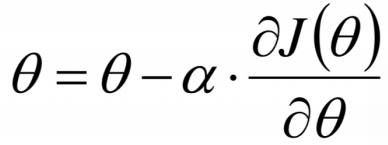
 损失函数每一点的切线（也就是斜率，就是梯度）推导如下：

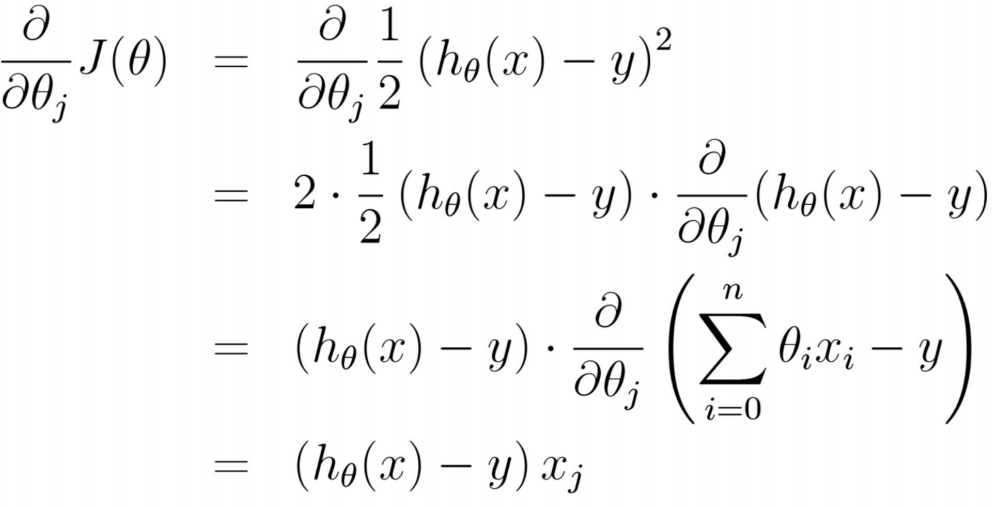
这里有梯度下降里面两种方法来迭代：

第一：批量梯度下降公式：

 

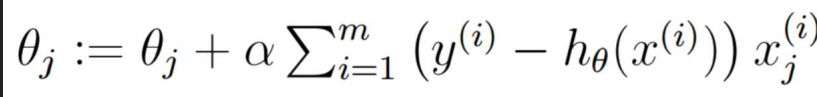
解剖公式：

所以总结如下：

每一个W调整都需要看每一个样本的梯度加和求平均。相当于看清每一条路，然后选择一个最好的。

1.每一次迭代每一个w调整的幅度是不一样的，每一轮迭代之间的每一轮对应的w0（可以推理到w1,w2,w3,w4...）也都是不一样的。

2.损失函数与w的图像中损失函数越小，每一组w与上一组w的差值也越来越小。如下图：

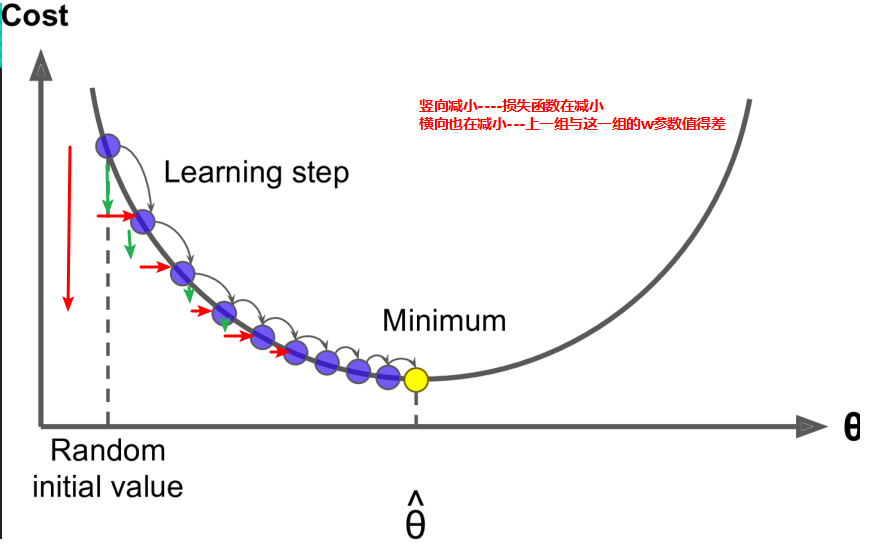
3.当Step(较小的时候)，也就是步长较小的时候如图，迭代次数比较多。

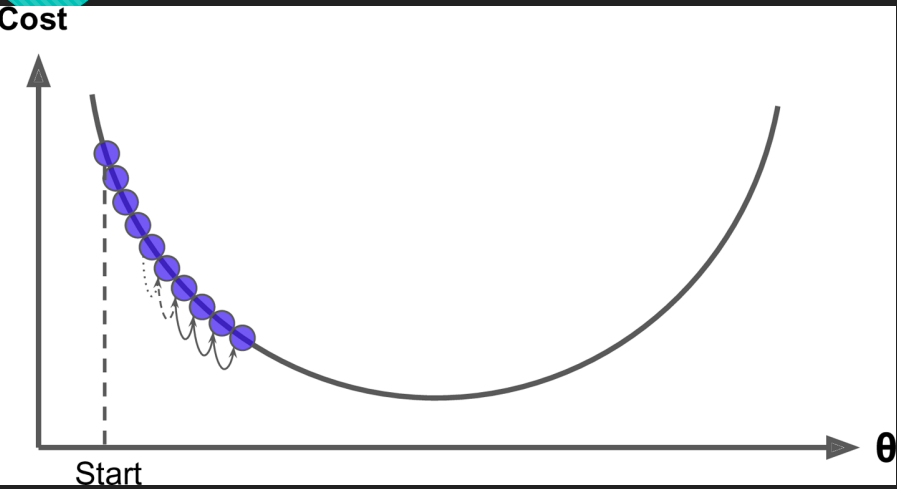
4.当Step(步长大的时候)，会来回震荡，但有可能找到全局最优解。

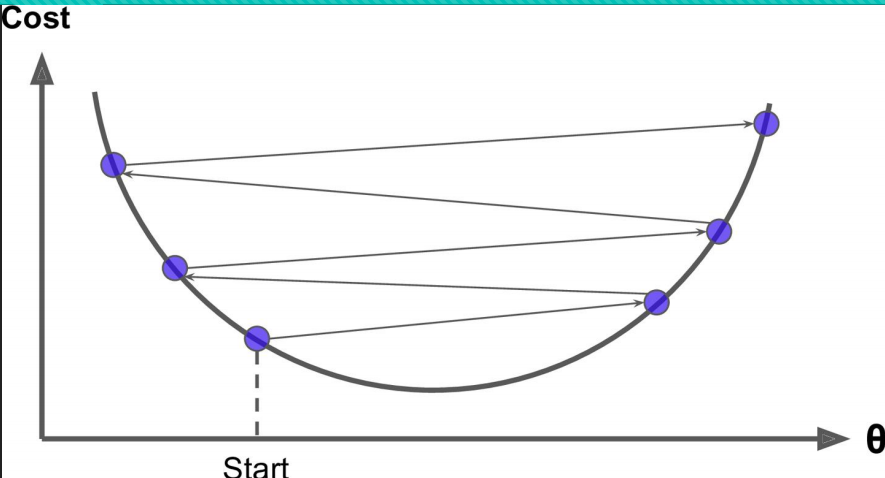
 5.梯度下降一般找到的是局部最优解，但模型一般堪用即可！！！！

 

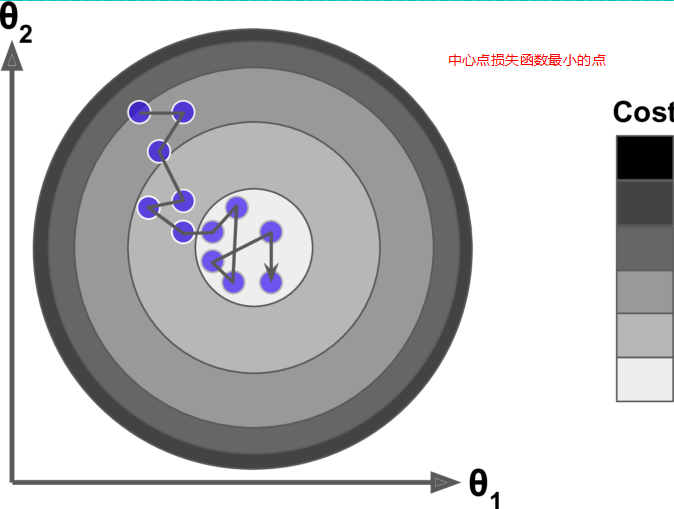
第二种：随机梯度下降（优先选择！！！！！）

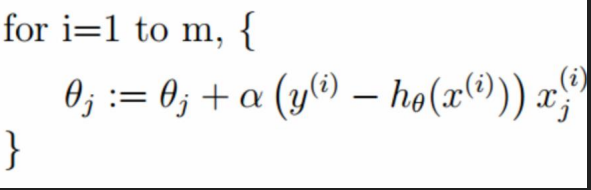
因为每一轮迭代不需要所有真实值与预测值的差再乘以所调整的w对应行的x的值，而是随机选择某一行计算.

举例求w0:

（真实值-预测值）*该行对应的第一列的x的值即可求得w0,w1也是随机找到一行对应相乘，这样一组w求完，本轮迭代结束。开始下一轮。

总结：

1.优先随机梯度下降，因为计算速度比较快。

2.随机梯度下降可以跳出局部最小值，因为有可能随机到某一行真实值和误差值相差较大，而对应的x也比较大，所以下降的幅度比较大，有可能找到最优解！！！

总结如下：

 三、具体代码

线性回归初始代码：

#!/usr/bin/python
# -*- coding: UTF-8 -*-
# 文件名: insurance.py

import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model


data = pd.read_csv('./data/insurance.csv')
print(type(data))
print(data.head())
print(data.tail())
# describe做简单的统计摘要
print(data.describe())
# 采样要均匀
data_count = data['age'].value_counts()
print(data_count)
data_count[:10].plot(kind='bar')#切片操作，取前10个，画直方图
plt.show()

print(data.corr())#皮尔逊相关系数 +1正相关 -1负相关 不能仅根据相关系数就把维度去掉

reg = linear_model.LinearRegression()
x = data[['age', 'sex', 'bmi', 'children', 'smoker', 'region']]
y = data['charges']
#python3.6 报错 sklearn ValueError: could not convert string to float: 'northwest'，加入一下几行解决
x = x.apply(pd.to_numeric, errors='coerce')
y = y.apply(pd.to_numeric, errors='coerce')
x.fillna(0, inplace=True)#如果碰到空值就转换成0
y.fillna(0, inplace=True)#如果碰到空值就转换成0

reg.fit(x, y)
print(reg.coef_)# w1,w2,w3...
print(reg.intercept_)#w0

 解析解求解：

#!/usr/bin/python
# -*- coding: UTF-8 -*-
# 文件名: linear_regression_0.py

import numpy as np
import matplotlib.pyplot as plt


X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]
print(X_b)

# 常规等式求解theta
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
print(theta_best)

X_new = np.array([[0], [2]])
X_new_b = np.c_[(np.ones((2, 1))), X_new]
print(X_new_b)
y_predict = X_new_b.dot(theta_best)
print(y_predict)

plt.plot(X_new, y_predict, 'r-')
plt.plot(X, y, 'b.')
plt.axis([0, 2, 0, 15])
plt.show()

根据公式自定义批量梯度下降。

import numpy as np

X = 2 * np.random.rand(100, 1)  # 随机取100个数，然后放到一列中去，是一个向量
y = 4 + 3 * X + np.random.randn(100, 1)  # randn 正态分布，（1列100行） 3，预测值  所以这里是真实值
X_b = np.c_[np.ones((100, 1)), X]  # 相当于100行两列，第一列全是1 ，第二列是一个随机的数
# print(X_b)

learning_rate = 0.22 #学习率，步长 学习率，步长 当学习率小的时候，可能每到最优点时就停止迭代了。
n_iterations = 1000  #迭代100次
m = 100  # 100行样本

theta = np.random.randn(2, 1)# 初始w值
count = 0

for iteration in range(n_iterations):# 0-999迭代
    count += 1
    gradients = 1/m * X_b.T.dot(X_b.dot(theta)-y)# 梯度 X_b.dot(theta)-y   是一个向量  X_b.T.dot乘以后面相当于矩阵的一个转置乘以一个向量相当于每一行会分别相乘加和。和
    theta = theta - learning_rate * gradients#每一次迭代，是一组数，相当于一组w参数都解出来了

print(count)
print(theta)

结果：

自定义随机梯度下降

import numpy as np


X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]
# print(X_b)

n_epochs = 50 #这些超参数都可以自己调整
t0, t1 = 5, 50  # 超参数

m = 100


def learning_schedule(t):
    return t0 / (t + t1)

theta = np.random.randn(2, 1) #初始一组w值

for epoch in range(n_epochs): # 50次 0-50
    for i in range(m): #100次 0-99
        random_index = np.random.randint(m) #随机取一行，拿到这一行的标号
        xi = X_b[random_index:random_index+1] #取这行的所有X值，切片左闭右开
        yi = y[random_index:random_index+1]#取这行的Y值
        gradients = 2*xi.T.dot(xi.dot(theta)-yi)#（误差-真实值）*这一行的x值
        learning_rate = learning_schedule(epoch*m + i) #epoch*m+i越来越大 带到上面函数中，学习率越来越小 让步长越来越小 不会随机太大
        theta = theta - learning_rate * gradients

print(theta)
#PS 总结：迭代次数多了，但每一次迭代不用加和，每一次的迭代计算小了

结果：

结

sk_learn中随机梯度下降公式

import numpy as np
from sklearn.linear_model import SGDRegressor

X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

sgd_reg = SGDRegressor(n_iter=50, penalty=None, eta0=0.1) # n_iter 步长  penalty  惩罚系数 eta0 最舒适的学习率，学习率不断下降
# print(X)
# print(y.ravel())# 相当于flat 压扁压平  多行一列的数据压扁成一行。。。一个行向量。
sgd_reg.fit(X, y.ravel()) #因为这个函数需要的y是一个行向量，所以压扁。

print(sgd_reg.intercept_, sgd_reg.coef_) # intercept_ w0   coef_ w1,w2,w3多个参数。

代码中sk_learn中学习率源码：可以发现学习率也是越来越小的。

PS：总结批量梯度下降里面我们要调整迭代次数和学习率，随机梯度下降里面我们要调整迭代次数和学习率，让学习率越来越小。