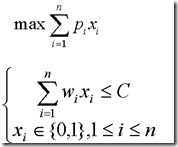来自:http://www.cnblogs.com/chinazhangjie/archive/2010/11/08/1871873.html
0-1背包问题
问题描述
给定n种物品和一背包。物品i的重量是wi,其价值为pi,背包的容量为C。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
0-1背包问题是一个特殊的整数规划问题。
例如:
最优解为:(1,0,1)
此时的价值为:6
算法的思想
首先,要对输入数据进行预处理,将各物品依其单位重量价值从大到小进行排列。
在下面描述的优先队列分支限界法中,节点的优先级由已装袋的物品价值加上剩下的最大单位重量价值的物品装满剩余容量的价值和。
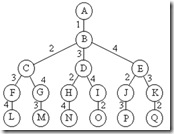
算法首先检查当前扩展结点的左儿子结点的可行性。如果该左儿子结点是可行结点,则将它加入到子集树和活结点优先队列中。当前扩展结点的右儿子结点一定是可行结点,仅当右儿子结点满足上界约束时才将它加入子集树和活结点优先队列。当扩展到叶节点时为问题的最优值。
上界函数
b = cp; // 初始化为目前背包的重量
// n表示物品总数,cleft为剩余空间
while (i <= n && w[i] <= cleft) {
cleft -= w[i]; // w[i]表示i所占空间
b += p[i]; // p[i]表示i的价值
i ++;
}
if (i <= n)
b += p[i] / w[i] * cleft; // 装填剩余容量装满背包
return b; // b为上界函数
主算法循环体
while (i != n+1) { // 非叶结点
// 检查当前扩展结点的左儿子结点
Typew wt = cw + w[i];
if (wt <= c) { // 左儿子结点为可行结点
if (cp+p[i] > bestp)
bestp = cp + p[i];
AddLiveNode(up, cp + p[i], cw + w[i], true, i+1);
}
up = Bound(i+1);
// 检查当前扩展结点的右儿子结点
if (up >= bestp) // 右子树可能含最优解
AddLiveNode(up, cp, cw, false, i+1);
// 取下一个扩展节点(略)
}
实现(略)