

/* 有循环节 */ #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define maxn 10000000 using namespace std; int a,b,n,T; int f[maxn]; inline int read() { int x=0,f=1;char c=getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } int main() { bool flag=false; a=read();b=read();n=read(); f[1]=1;f[2]=1;f[3]=(a+b)%7; for(int i=4;i<=n;i++) { f[i]=(a*f[i-1]+b*f[i-2])%7; if(f[i-1]==1&&f[i]==1) {flag=true;T=i-2;break;} } if(!flag) printf("%d",f[n]); else { int pos=n%T;if(pos==0) pos=T; printf("%d",f[pos]); } return 0; }

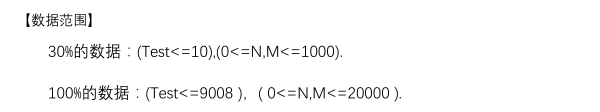
/* 转化为二维平面上 左下角走到右上角不经过对角线的路径条数 卡特兰数列 */ #include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define inf 100000000 #define ll long long #define RG register int #define rep(i,a,b) for(RG i=a;i<=b;i++) #define per(i,a,b) for(RG i=a;i>=b;i--) using namespace std; int T; double n,m; inline int read() { int x=0,f=1;char c=getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } int main() { T=read(); while(T--) { n=read();m=read(); if(n<m) {puts("0.000000");continue;} double _1=n-m+1,_2=n+1; printf("%.6lf ",_1/_2); } return 0; }

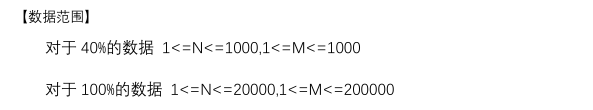
/* Tarjan缩点后是一棵树 求树的直径并维护每个点到直径两端点的最大值。 三遍dfs即可 */ #include<bits/stdc++.h> #define maxn 20005 #define maxm 200005 using namespace std; int n,m,id,dfn[maxn],low[maxn],head[maxn],head2[maxn],cnt; int dis[maxn],dis1[maxn],mx=0,root; int belong[maxn],belnum; bool vis[maxn]; stack<int> stk; struct Edge{ int u,v,val,next; }edge[maxm<<1],e[maxm<<1]; inline int read() { int x=0,f=1;char c=getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } namespace Tarjan { inline void add(int u,int v,int val) { edge[++cnt].v=v; edge[cnt].u=u; edge[cnt].val=val; edge[cnt].next=head[u]; head[u]=cnt; } inline void tarjan(int u,int fa) { dfn[u]=low[u]=++id; vis[u]=1; stk.push(u); for(int i=head[u];i!=-1;i=edge[i].next) { int v=edge[i].v; if(!dfn[v]) { tarjan(v,u); low[u]=min(low[u],low[v]); } else if(vis[v]&&v!=fa) { low[u]=min(low[u],dfn[v]); } } if(dfn[u]==low[u]) { belnum++; int temp; do{ temp=stk.top(); belong[temp]=belnum; vis[temp]=0; stk.pop(); }while(temp!=u); } } inline void solve1() { memset(head,-1,sizeof(head)); for(int i=1,u,v,val;i<=m;i++) { u=read();v=read();val=read(); add(u,v,val);add(v,u,val); } for(int i=1;i<=n;i++) { if(!dfn[i]) tarjan(i,0); } } } namespace LP { inline void Add(int u,int v,int val) { e[++cnt].v=v; e[cnt].val=val; e[cnt].next=head2[u]; head2[u]=cnt; } void dfs1(int u,int fa) { for(int i=head2[u];i!=-1;i=e[i].next) { int v=e[i].v; if(v==fa) continue; dis[v]=dis[u]+e[i].val; if(dis[v]>mx) mx=dis[v],root=v; dfs1(v,u); } } void dfs2(int u,int fa) { for(int i=head2[u];i!=-1;i=e[i].next) { int v=e[i].v; if(v==fa) continue; dis1[v]=dis1[u]+e[i].val; dfs2(v,u); } } inline void solve2() { cnt=0; memset(head2,-1,sizeof(head2)); for(int i=1;i<=n;i++) for(int j=head[i];j!=-1;j=edge[j].next) { if(belong[i]!=belong[edge[j].v]) Add(belong[i],belong[edge[j].v],edge[j].val); } dfs1(1,-1); mx=0;memset(dis,0,sizeof(dis)); dfs1(root,-1); mx=0; dfs2(root,-1); for(int i=1;i<=n;i++) printf("%d ",max(dis[belong[i]],dis1[belong[i]])); } } int main() { freopen("prize.in","r",stdin); freopen("prize.out","w",stdout); n=read();m=read(); Tarjan::solve1(); LP::solve2(); return 0; }