难度:☆☆☆☆☆☆☆☆



/* 对于第一问:f[i][j]表示前i个数,当前黑板上的数为j的概率 当前有三种情况 1.当前数不是j的倍数—>黑板上的数字改变。 2.当前数是j的倍数且当前数在前i个数中(已经选过) 3.当前数是j的倍数且没有选过 转移:f[i+1][j]=((j的倍数个数-i)*f[i][j]+f[i][gcd(j,k)]) 的平均值 j的倍数个数-i是没选过的j的倍数。 对于第二问,考虑博弈论中sg函数。可知sg[i][1]二维含义同f数组)必定为0(最后黑板上剩下1必败) sg[n][i]=0(选完了必败) 同样枚举上述三种情况,取后续状态mex值即可。 */ #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define eps 1e-8 #define N 1000 using namespace std; inline int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); } int sg[N + 5][N + 5], g[N + 5][N + 5], f[N + 5], n, a[N + 5]; double dp[N + 5][N + 5], ans = 0; bool getsg(int x, int y) { if (x == 1) return 1; if (sg[x][y] != -1) return sg[x][y]; bool flag = 1; if (f[x] > y) flag &= getsg(x, y + 1); for (int i = 1; i <= n; i++) if (g[x][i] != x) flag &= getsg(g[x][i], y + 1); sg[x][y] = !flag; return sg[x][y]; } int main() { freopen("cards.in", "r", stdin); freopen("cards.out", "w", stdout); scanf("%d", &n); int mx = 0; for (int i = 1; i <= n; i++) { scanf("%d", a + i); mx = max(mx, a[i]); g[0][i] = a[i]; } for (int i = 1; i <= mx; i++) for (int j = 1; j <= n; j++) f[i] += (a[j] % i == 0), g[i][j] = gcd(i, a[j]); dp[0][0] = 1; for (int i = 1; i <= n; i++) for (int j = 0; j <= mx; j++) if (dp[i - 1][j] > eps) { dp[i][j] += dp[i - 1][j] * (f[j] - i + 1) / (n - i + 1); for (int k = 1; k <= n; k++) if (g[j][k] != j) { if (g[j][k] != 1) dp[i][g[j][k]] += dp[i - 1][j] / (n - i + 1); else ans += (i + 1 & 1) * dp[i - 1][j] / (n - i + 1); } } if (n & 1) for (int j = 0; j <= mx; j++) ans += dp[n][j]; printf("%.9lf ", ans); memset(sg, -1, sizeof(sg)); if (getsg(0, 0)) puts("1.000000000"); else puts("0.000000000"); return 0; }



/* 对于60~80分,可以n^2暴力,断掉每条边时,O(N)求每个部分的直径,然后相乘。 正解:倒序加边,考虑两棵树合并的时候新直径一定是原来两个直径四个断点任意两个的路径。 所以可以首先求LCA倍增处理两点间路径,然后求最大。更新答案要用逆元。 */ #include<iostream> #include<cstdio> #include<cstring> #define N 100007 #define mod 1000000007 #define ll long long using namespace std; int a[N],dep[N],sum[N],fa[N][20],head[N],del[N]; int D[N][2],ans[N],f[N],len[N],end[2]; int n,m,pre,cnt; struct edge{ int u,v,net; }e[N<<1]; inline int read() { int x=0,f=1;char c=getchar(); while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } inline void add(int u,int v) { e[++cnt].u=u;e[cnt].v=v;e[cnt].net=head[u];head[u]=cnt; } void dfs(int u,int from) { fa[u][0]=from;dep[u]=dep[from]+1; sum[u]=sum[from]+a[u]; for(int i=1;i<=19;i++) fa[u][i]=fa[fa[u][i-1]][i-1]; for(int i=head[u];i;i=e[i].net) { int v=e[i].v; if(v!=from)dfs(v,u); }return; } int find(int x) { return x==f[x]?x:f[x]=find(f[x]); } int ksm(int a,int b) { int res=1; while(b) { if(b&1) res=1ll*res*a%mod; b>>=1;a=1ll*a*a%mod; }return res%mod; } int lca(int u,int v) { if(dep[u]<dep[v]) swap(u,v); int t=dep[u]-dep[v]; for(int i=0;i<20;i++) if(t&(1<<i)) u=fa[u][i]; if(u==v) return u; for(int i=19;i>=0;i--) { if(fa[u][i]!=fa[v][i]) { u=fa[u][i]; v=fa[v][i]; } }return fa[u][0]; } int getlen(int u,int v) { int L=lca(u,v); return sum[u]+sum[v]-2*sum[L]+a[L]; } int main() { freopen("forest.in","r",stdin); freopen("forest.out","w",stdout); int x,y; n=read();pre=1; for(int i=1;i<=n;i++) { a[i]=read();f[i]=i; pre=(ll)pre*a[i]%mod; D[i][0]=D[i][1]=i;len[i]=a[i]; } for(int i=1;i<n;i++) { x=read();y=read(); add(x,y);add(y,x); } dfs(1,0);int t=n;ans[n]=pre; for(int i=1;i<n;i++) del[i]=read(); for(int i=n-1;i;i--) { int id=del[i],u=e[id*2-1].u,v=e[id*2-1].v; u=find(u);v=find(v); if(len[u]<len[v]) swap(u,v); int tmax=len[u]; for(int j=0;j<2;j++) end[j]=D[u][j]; for(int j=0;j<2;j++) for(int k=0;k<2;k++) { int l=getlen(D[u][j],D[v][k]); if(l>tmax) { tmax=l; end[0]=D[u][j];end[1]=D[v][k]; } } pre=(ll) pre*ksm(len[u],mod-2)%mod; pre=(ll) pre*ksm(len[v],mod-2)%mod; f[v]=u;len[u]=tmax; for(int j=0;j<2;j++) D[u][j]=end[j]; pre=(ll) pre*len[u]%mod; ans[--t]=pre; } for(int i=1;i<=n;i++) printf("%d ",ans[i]); return 0; }


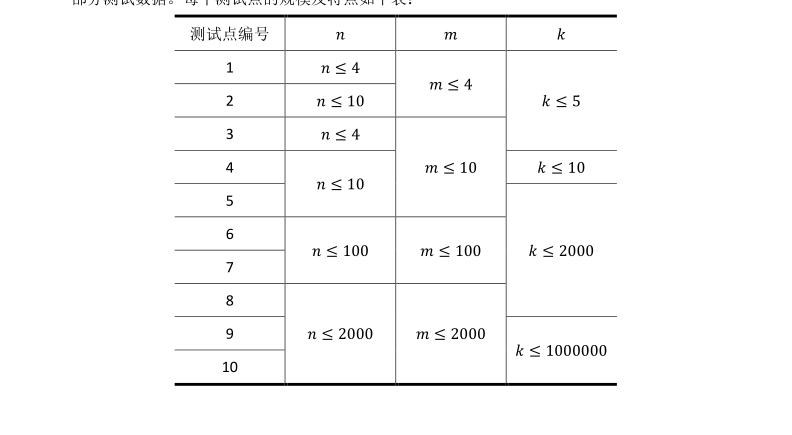
/* 这题确实是恶心,并且貌似没有部分分...... 让我们来瞻仰一下std做法 考虑两列的情况。若两列颜色分别为A,B,则A独有的颜色就是A—A∩B ,B同理。 若是多列那还是设两边两列为A,B,中间多列为C,那根据题目结论可以知道C一定是A∩B的子集。枚举A中独有颜色个数,B中独有颜色个数与A中相同。若有j独有,i共有C(K,i)*C(k-i+1,j)*C(k-i-j,j) 因为每次选择都必须是恰好那些颜色,不能少,所以用总方案数减去不是恰好的就可以了。 */ # include<iostream> # include<cstdio> # include<cstring> # include<cstdlib> using namespace std; const int pp=1000000007; int c[2008][2008],f[2008],p[2008],ni[2008]; int n,m,k,nn; inline int power(int x,int n) { int ans=1,tmp=x; while (n) { if (n&1) ans=(long long)ans*tmp%pp; tmp=(long long)tmp*tmp%pp;n>>=1; } return ans; } void Count_c() { for (int i=0;i<=nn;i++) c[i][0]=1; for (int i=1;i<=nn;i++) for (int j=1;j<=i;j++) { c[i][j]=c[i-1][j-1]+c[i-1][j]; if (c[i][j]>=pp) c[i][j]-=pp; } } void Count_p() { int mm=(m-2)*n; for (int i=0;i<=nn;i++) p[i]=power(i,mm); } void Count_f() { f[0]=0;f[1]=1; for (int i=2;i<=nn;i++) { f[i]=power(i,n); for (int j=1;j<i;j++) { f[i]-=(long long)f[j]*c[i][j]%pp; if (f[i]<=-pp) f[i]+=pp; } if (f[i]<0) f[i]+=pp; } } void Count_ni() { ni[1]=1; for (int i=2;i<=nn;i++) ni[i]=power(i,pp-2); } int main() { freopen("photo.in","r",stdin); freopen("photo.out","w",stdout); scanf("%d%d%d",&n,&m,&k); nn=min(n,k); if (m==1) printf("%d ",power(k,n)); else { Count_c();Count_p(); Count_f();Count_ni(); long long tmp=1,tmp1=1,sum=0,sum1; for (int s=1;s<=nn;s++) { tmp=tmp*ni[s]%pp; tmp=tmp*(k-s+1)%pp; tmp1=1;sum1=0; for (int j=0;j<=s;j++) { sum1+=tmp1*c[s][s-j]%pp*p[s-j]%pp; if (sum1>=pp) sum1-=pp; tmp1=tmp1*ni[j+1]%pp; if (k-s<j+1) break; tmp1=tmp1*(k-s-j)%pp; } sum+=tmp*f[s]%pp*f[s]%pp*sum1%pp; if (sum>=pp) sum-=pp; } printf("%d ",sum); } fclose(stdin); fclose(stdout); return 0; }