
难度:☆☆☆☆☆☆☆

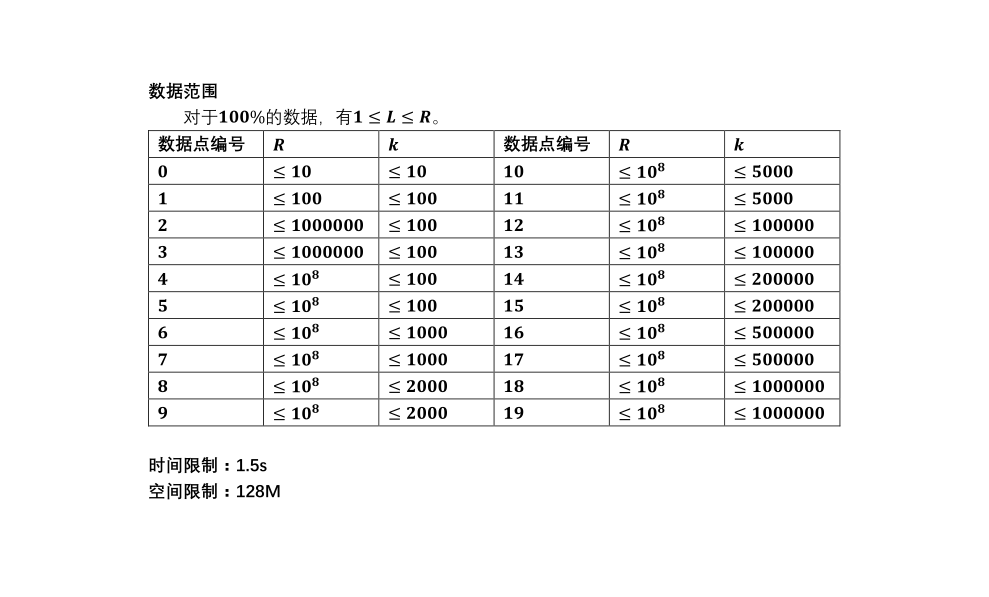
题解: 有个定理,另sum(x)表示小于等于x的数中与x互质的数的和
sum(x)=φ(x)*x/2 最后可知f(x)=x (f(1)=2) 当然打表能知道。
然后就转化为了求Σi^k
然后就是拉格朗日插值法了,不在我理解范畴........
但这个博客介绍挺好哒 http://www.cnblogs.com/ECJTUACM-873284962/p/6833391.html
std:
#include <cstring>
#include <ctime>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
using namespace std;
const int Mod=998244353;
const int MAXK=1000000;
int power(int x,int k)
{
int ret=1;
while (k)
{
if (k&1) ret=1LL*ret*x%Mod;
x=1LL*x*x%Mod;
k>>=1;
}
return ret;
}
int k;
int f[MAXK+10];
int pre[MAXK+10],suf[MAXK+10];
int jc[MAXK+10],K[MAXK+10];
int cnt(int n)
{
if (n==0) return 0;
int ans=0;
if (n<=k+10 || n<=MAXK)
{
for (int i=1; i<=n; i++) ans=(K[i]+ans)%Mod;
}
else
{
pre[0]=1;
for (int i=1; i<=k+2; i++) pre[i]=1LL*pre[i-1]*(n-i)%Mod;
suf[k+3]=1;
for (int i=k+2; i>=1; i--) suf[i]=1LL*suf[i+1]*(n-i)%Mod;
int l=k+1,r=0,flag=((k+1)&1)?(-1):(1);
for (int i=1; i<=k+2; i++)
{
int s=1LL*pre[i-1]*suf[i+1]%Mod,m=1LL*(flag*jc[l]+Mod)*jc[r]%Mod;
ans=(1LL*f[i]*s%Mod*power(m,Mod-2)%Mod+ans)%Mod;
l--;
r++;
flag*=-1;
}
}
ans=((ans+K[2])%Mod-1+Mod)%Mod;
return ans;
}
int L,R;
void init()
{
cin>>L>>R>>k;
for (int i=1; i<=MAXK+5; i++) K[i]=power(i,k);
jc[0]=1;
for (int i=1; i<=k+2; i++) jc[i]=1LL*jc[i-1]*i%Mod;
for (int i=1; i<=k+2; i++) f[i]=(f[i-1]+K[i])%Mod;
cout<<(cnt(R)-cnt(L-1)+Mod)%Mod;
return ;
}
int main()
{
freopen("count.in","r",stdin);
freopen("count.out","w",stdout);
init();
fclose(stdin);
fclose(stdout);
//fprintf(stderr,"%.3lf
",1.0*clock()/(1.0*CLOCKS_PER_SEC));
return 0;
}

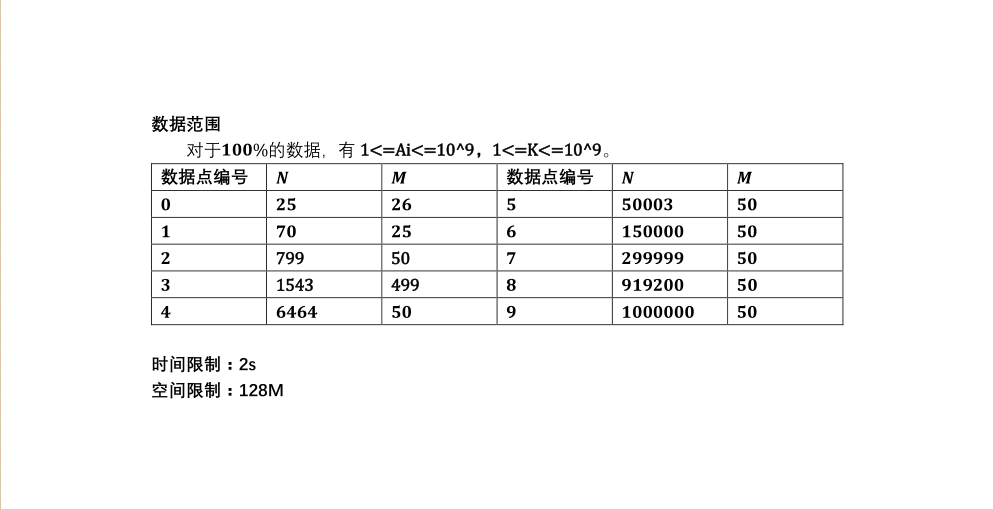
/* 题意转化为求最大的区间长度使得这段区间和减k>=0 首先做前缀和,可知若当前到了k,i<j<k && sum[i]<sum[j]则j一定不可能比i更优 用单调栈维护这个过程。然后倒序更新答案即可。 */ #include<iostream> #include<cstdio> #include<cstring> #define N 1000007 using namespace std; long long sum[N]; int a[N],st[N],top,n,m,cnt; inline int read() { int x=0,f=1;char c=getchar(); while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } void solve(int k) { top=1;int res=0; for(int i=1;i<=n;i++) { sum[i]=sum[i-1]+a[i]-k; if(!top || sum[st[top]]>sum[i]) st[++top]=i; } for(int i=n;i>=1;i--) { while(top && sum[i]>=sum[st[top]]) top--; res=max(res,i-st[top+1]); } printf("%d ",res); } int main() { freopen("blocks.in","r",stdin); freopen("blocks.out","w",stdout); n=read();m=read(); for(int i=1;i<=n;i++) a[i]=read(); while(m--) solve(read()); return 0; }



/* 将字符串倒序插入trie树,问题就转换成了若干字符串结束的LCA深度 倍增维护LCA,每插入一个字符串,处理一次fa数组就可以了 当然这题也可以哈希+二分 */ #include<iostream> #include<cstdio> #include<cstring> #define N 100007 #define M 1000007 using namespace std; int Log[N],pos[N]; int n,m,len,cnt,sum; char last[N],str[N]; struct Trie { int s[26],f[27]; int dep; }tr[M]; inline int read() { int x=0,f=1;char c=getchar(); while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } void insert(int x) { last[x]=str[len-1]; int now=1; for(int i=len-1;i>=0;i--) { int id=str[i]-'a'; if(!tr[now].s[id]) { tr[now].s[id]=++cnt; tr[cnt].f[0]=now; tr[cnt].dep=tr[now].dep+1; for(int i=1;i<=27;i++) { tr[cnt].f[i]=tr[tr[cnt].f[i-1]].f[i-1]; if (tr[cnt].f[i]==0) break;//再往后跳也不可能有f值. } }now=tr[now].s[id]; }pos[x]=now; } inline void init() { for(int i=1,now=-1,next=1;i<=N;i++) { if(i==next) now++,next<<=1; Log[i]=now; } } int up(int x,int step) { while (step) { int up=Log[step]; x=tr[x].f[up]; step-=(1<<up); } return x; } int LCA(int x,int y) { if(tr[x].dep>tr[y].dep) x=up(x,tr[x].dep-tr[y].dep); else y=up(y,tr[y].dep-tr[x].dep); if(x==0 || y==0) puts("myjdsb"); int k=Log[tr[x].dep]; while(x!=y) { while(k>=0 && tr[x].f[k]==tr[y].f[k]) k--; if(k==-1) return tr[x].f[0]; x=tr[x].f[k];y=tr[y].f[k]; }return x; } int main() { freopen("biology.in","r",stdin); freopen("biology.out","w",stdout); init(); n=read();m=read();cnt=1;sum=0; for(int i=1;i<=n;i++) { scanf("%s",str); len=strlen(str); sum+=len;insert(i); } while(m--) { int ty=read(); if(ty==1) { scanf("%s",str); len=strlen(str); insert(++n); } else { int T=read(),ans=0; while(T--) { int x=read(); if(!ans) ans=pos[x]; else ans=LCA(ans,pos[x]); } printf("%d ",tr[ans].dep); } } return 0; }