题面
题意
你有(n)个红点,(m)个蓝点,每个点至少要向一个和它颜色不同的点连一条边,两点之间连边的代价是他们的距离,求合法方案的最小代价。
题解
首先这是一个假的交互题(只输入一次交互没有意义)。
考虑sub2怎么做:如果红色全部在蓝色前面,那么我们配对的方式一定是这样的:
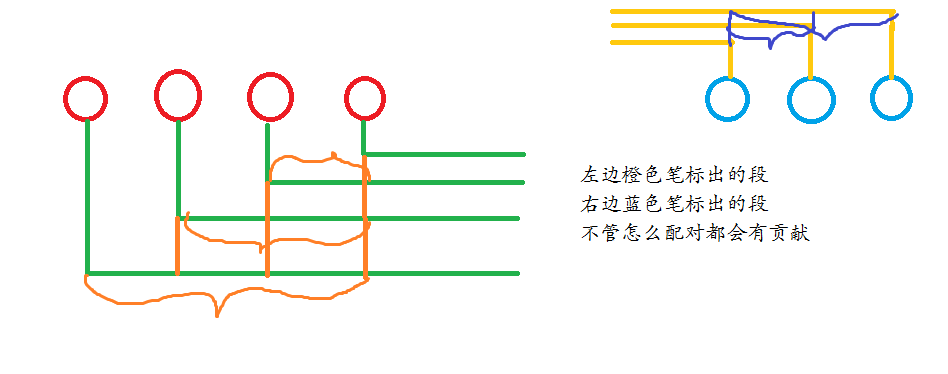
那么答案肯定是(sum_{i=1}^n red_n-red_i + sum_{i=1}^m blue_i-blue_1)
再考虑中间怎么配对,很明显是(max(n,m) imes (blue_1-red_n)),因为每个点都至少要连一条线出去,所以中间那段被走了(max (n,m))次。
这个是可以通过预处理前缀和(O(1))解决问题的。
但是现在是红蓝交错的,我们考虑把序列划分成一些小段,使得这些小段内红的严格在蓝的前面,然后就变成了上面那种情况。
那么考虑dp,设(f_i)表示某一个划分结束在(i)处,可以获得的最优代价,由于在(n)处肯定要结束,所以最终答案肯定是(f_n)。
如果当前和上一个颜色一样就更新连续的段数与和,如果不一样就考虑从上一个颜色不同的位置到这一个位置这一段内dp值的更新。如果某一段是单独一个的那肯定不能分割,(f_i=inf),否则就由上一个分割点转移过来,转移过程中的代价就按照上式来计算。
代码
#include "wiring.h"
#define it register int
#define ct const int
#define il inline
using namespace std;
typedef long long ll;
const int N = 1000005;
const ll inf = 1e18;
int c[N], col[N], cnt, l[N], r[N], n, m;
ll f[N], sum[N], g[N], mn[N];
il ll Min(const ll p, const ll q) { return p < q ? p : q; }
il ll min_total_length(vector<int> a, vector<int> b) {
ct n = a.size(), m = b.size();
it i = 0, j = 0, cn = 0, len;
register ll x, s;
while (i < n && j < m) a[i] < b[j] ? c[++cn] = a[i++], col[cn] = 1 : (c[++cn] = b[j++], col[cn] = 2);
while (i < n) c[++cn] = a[i++], col[cn] = 1;
while (j < m) c[++cn] = b[j++], col[cn] = 2;
for (i = 1; i <= cn; i = j) {
for (j = i; col[i] == col[j] && j <= cn; ++j);
l[++cnt] = i, r[cnt] = j - 1;
}
for (i = l[1]; i <= r[1]; ++i) f[i] = inf;
for (i = 2; i <= cnt; ++i) {
for (j = r[i - 1]; j >= l[i - 1] - 1; --j)
sum[j] = sum[j + 1] + c[r[i - 1]] - c[j], g[j] = sum[j + 1] + f[j],
mn[j] = g[j] + (0ll + c[l[i]] - c[r[i - 1]]) * (r[i - 1] - j);
for (j = r[i - 1] - 1; j >= l[i - 1] - 1; --j) g[j] = Min(g[j], g[j + 1]);
for (j = l[i - 1]; j <= r[i - 1]; ++j) mn[j] = Min(mn[j], mn[j - 1]);
x = c[l[i]] - c[r[i - 1]], s = 0;
for (j = l[i]; j <= r[i]; ++j)
s += c[j] - c[l[i]], len = j - l[i] + 1,
f[j] = s + (l[i - 1] <= r[i - 1] - len + 1? Min(x * len + g[r[i - 1] - len + 1], mn[r[i - 1] - len]): g[l[i - 1] - 1] + x * len);
}
return f[cn];
}