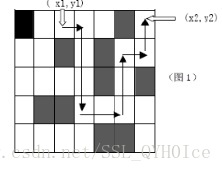
题目描述
给出一张地图,这张地图被分为n×m(n,m<=100)个方块,任何一个方块不是平地就是高山。平地可以通过,高山则不能。现在你处在地图的(x1,y1)这块平地,问:你至少需要拐几个弯才能到达目的地(x2,y2)?你只能沿着水平和垂直方向的平地上行进,拐弯次数就等于行进方向的改变(从水平到垂直或从垂直到水平)的次数。例如:如图,最少的拐弯次数为5。
Solution
这个题想了我一会啊... 所以来记录一下.
想法:
直接从起点开始跑广搜.
但是与传统广搜不同的是,一跑就把那一整行都跑掉,然后全部压入队列中.
然后同时将这一行都打上标记.也就是说这个时候我们的方向是固定的.
具体感受一下代码吧... 我基础是真的弱鸡.
Code
/*
Problem : 1584
Time : Day -95
*/
#include<bits/stdc++.h>
using namespace std;
const int dx[]={0,1,0,-1};
const int dy[]={1,0,-1,0};
struct sj{
int x,y,turn;
}s,t,p;
queue<sj> q;
int n,m,c[101][101];
bool v[101][101];
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&c[i][j]);
scanf("%d%d%d%d",&s.x,&s.y,&t.x,&t.y);
q.push(s);
memset(v,0,sizeof(v));
q.front().turn=0;
while(!q.empty())
{
for(int i=0;i<4;i++)
{
p.x=q.front().x+dx[i];
p.y=q.front().y+dy[i];
while(p.x>0&&p.x<=n&&p.y>0&&p.y<=m&&!c[p.x][p.y])
{
if(!v[p.x][p.y])
{
if(p.x==t.x&&p.y==t.y)
{
printf("%d
",q.front().turn);
return 0;
}
v[p.x][p.y]=1;
p.turn=q.front().turn+1;
//cout<<p.x<<' '<<p.y<<endl;
q.push(p);
}
//cout<<p.x<<' '<<p.y<<endl;
p.x+=dx[i];
p.y+=dy[i];
}
}
q.pop();
}
}