题目描述
这是一个流行在Jsoi的游戏,名称为祖玛。
精致细腻的背景,外加神秘的印加音乐衬托,彷佛置身在古老的国度里面,进行一个神秘的游戏——这就是著名的祖玛游戏。祖玛游戏的主角是一只石青蛙,石青蛙会吐出各种颜色的珠子,珠子造型美丽,并且有着神秘的色彩。
环绕着石青蛙的是载着珠子的轨道,各种颜色的珠子会沿着轨道往前滑动,石青蛙必需遏止珠子们滚进去轨道终点的洞里头,如何减少珠子呢?就得要靠石青蛙吐出的珠子与轨道上的珠子相结合,颜色相同者即可以消失得分!直到轨道上的珠子通通都被清干净为止。 或许你并不了解祖玛游戏。没关系。这里我们介绍一个简单版本的祖玛游戏规则。一条通道中有一些玻璃珠,每个珠子有各自的颜色,如图1所示。玩家可以做的是选择一种颜色的珠子(注意:颜色可以任选,这与真实游戏是不同的)射入某个位置。
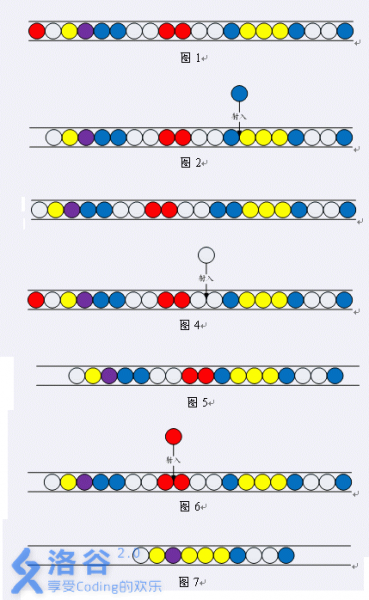
图1 图2中玩家选择一颗蓝色珠子,射入图示的位置,于是得到一个图3的局面。
图2 图3 当玩家射入一颗珠子后,如果射入的珠子与其他珠子组成了三颗以上连续相同颜色的珠子,这些珠子就会消失。例如,将一颗白色珠子射入图4中的位置,就会产生三颗颜色相同的白色珠子。这三颗珠子就会消失,于是得到图5的局面。
图4 图5 需要注意的一点是,图4中的三颗连续的黄色珠子不会消失,因为并没有珠子射入其中。 珠子的消失还会产生连锁反应。当一串连续相同颜色的珠子消失后,如果消失位置左右的珠子颜色相同,并且长度大于2,则可以继续消失。例如,图6中,射入一颗红色珠子后,产生了三颗连续的红色珠子。当红色珠子消失后,它左右都是白色的珠子,并且一共有四颗,于是白色珠子也消失了。之后,消失位置的左右都是蓝色珠子,共有三颗,于是蓝色珠子也消失。最终得到图7的状态。注意,图7中的三颗黄色珠子不会消失,因为蓝色珠子消失的位置一边是紫色珠子,另一边是黄色珠子,颜色不同。
图6 图7 除了上述的情况,没有其他的方法可以消去珠子。 现在,我们有一排珠子,需要你去消除。对于每一轮,你可以自由选择不同颜色的珠子,射入任意的位置。你的任务是射出最少的珠子,将全部珠子消去。
Solution
这是本蒟蒻博主自己想出来的第一道省选DP.想了一整天啊 QAQ...
这道题的主要难度是对题意的理解,即要找出这个题目的最关键特点.
通过题面可以知道,在一个序列中,如果有连续的一段颜色,那么无论怎么样,在最终合并的时候,它们都不会被分开的.
然后又鉴于它颜色的种类可能很大,开不下那么大的数组,所以我们就在DP前需要进行一次预处理.
一个是把颜色离散(这个其实也没必要),第二个就是要把所有连续的颜色相同的点都处理在一起,形成一个新的序列.
同时在这个新的序列中我们要记录每一个新的元素包含的节点个数,这是为了满足游戏规则里的至少要三个才能合并的条件.
然后这之后就是一个较为简单的区间DP
枚举i j 和断点 k.
然后这个时候有两种情况可以合并:
1. 直接 i -> k 和 k+1 -> j 两段合并.
2. 中间的先合并,然后两边合并,连锁反应.
Ps: 原题里有一个比较坑的数据点 在讨论版里面. 所以有特判.
代码
#include<bits/stdc++.h> using namespace std; const int maxn=508; int n,len,f[maxn][maxn],pd[maxn]; int c[maxn],num,a[maxn],col[maxn],newt[maxn]; void pre() { sort(a+1,a+n+1); for(int i=1;i<=n;) { int xx=a[i],flag=1; col[++num]=xx; while(a[i+flag]==xx) flag++; i+=flag; } for(int i=1;i<=n;i++) for(int j=1;j<=num;j++) if(c[i]==col[j]) {c[i]=j;break;} for(int i=1;i<=n;) { int xx=c[i]; int flag=1; while(c[i+flag]==xx) flag++; newt[++len]=xx; pd[len]=flag; f[len][len]=(flag!=1)?1:2; i+=flag; } } int main() { scanf("%d",&n); if(n==17){cout<<2<<endl;return 0;} for(int i=1;i<=n;i++) scanf("%d",&a[i]),c[i]=a[i]; memset(f,0x7f,sizeof(f)); pre(); for (int i=1;i<=len-1;++i) for (int j=1;j<=len-i;++j) { if (newt[j]==newt[j+i]) if (i==1) f[j][j+i]=pd[j]+pd[j+i]>=2?1:2; else f[j][j+i]=f[j+1][j+i-1]+(pd[j]+pd[j+i]>=3?0:1); for (int k=j;k<j+i;++k) f[j][j+i]=min(f[j][j+i],f[j][k]+f[k+1][j+i]); } cout<<f[1][len]<<endl; }