3661: Hungry Rabbit
Time Limit: 100 Sec Memory Limit: 512 MBSec Special Judge
Submit: 67 Solved: 47Description
可怕的洪水在夏天不期而至,兔子王国遭遇了前所未有的饥荒,它们不得不去外面的森林里寻找食物。
为了简化起见,我们假设兔子王国中有n只兔子,编号为1n。在救济粮到来之前的m天中,每天恰好有k只兔子需要去森林里寻找粮食。森林里居住着可怕的大灰狼,所幸兔子已经摸清了大灰狼捕食习惯,即狼们在每一天只会捕食特定编号的兔子。为了安全起见,兔子们需要保证每次出去觅食的k只兔子都不会被狼捕食。由于每天出去捕食的兔子都不尽相同,它们为每一天定义了一个生疏度pi,即第i天出来寻找食物,但是第i1天却没有出来觅食的兔子个数。规定第1天的生疏度为0.现在兔子们希望在保证安全的前提下,每天的生疏度不能超过L,请为兔子们构造一个合法的方案。Input
第一行包括四个整数n,m,k和L.
接下来n行,每行一个长度为m的01串。其中第i行第j个字符若为0,则表示狼在第j天会捕食编号为i的兔子,为1则表示不捕食。Output
m行,每行k个1-n之间互不相同的整数,代表这一天出去寻找食物的兔子编号。如果没有合法方案,则输出一行1即可。
Sample Input
5 4 3 1
1001
1101
1111
1110
0111
Sample Output
2 3 4
2 3 4
3 4 5
2 3 5
HINT
对于 100% 的测试数据,1 <= n;m <= 800; 1 <= k <= n; 1 <= l <= k
Source
【分析】
唉、、、我打了网络流,70分。。。【其实数据弱恰好我数组开小本来90分的。。
说说我的网络流打法吧,毕竟想了很久。
就是1100011的兔子可以看成两只1100000、0000011的兔子。
然后就是说每个兔子表示一个区间,表示它可以从l~r这几天工作。
就是要找若干个区间覆盖全区间k次。
就类似这样子的建图:
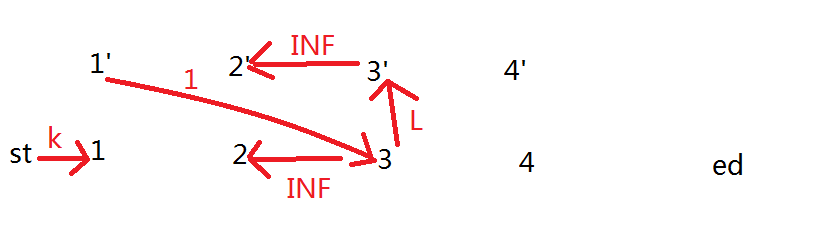
拆点那里的点容限制了<=L次交换。反向INF表示区间相交求并集。然后判断是否满流就是否有解。
然后有意义的表示区间的边就是答案,输出即可。【好像输出答案有点困难啊??
然后正解是贪心!【表示考场上想过不知道为什么脑抽觉得n^2log过不了???【黑人问号???
就是每次贪心找尽量长的区间。。。
有优先队列维护,每次用最优的更新最差的看看是否成立即可。

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 #include<queue> 7 using namespace std; 8 #define Maxn 810 9 #define INF 0xfffffff 10 11 struct node 12 { 13 int l,r,id; 14 }t[Maxn*Maxn]; 15 struct cmp{bool operator()(node x,node y){return x.r<y.r;}}; 16 struct cmp2{bool operator()(node x,node y){return x.r>y.r;}}; 17 // bool cmp(node x,node y) {return x.r>y.r;} 18 // bool cmp2(node x,node y) {return x.r<y.r;} 19 bool cmp3(node x,node y) {return x.l<y.l;} 20 priority_queue<node,vector<node>,cmp> q1; 21 priority_queue<node,vector<node>,cmp2> q2; 22 23 char s[Maxn]; 24 25 bool vis[Maxn]; 26 int op[Maxn][Maxn]; 27 int main() 28 { 29 // int T; 30 // scanf("%d",&T); 31 // while(T--) 32 { 33 int n,m,k,l; 34 scanf("%d%d%d%d",&n,&m,&k,&l); 35 36 int cnt=0,id; 37 for(int i=1;i<=n;i++) 38 { 39 scanf("%s",s+1); 40 for(int j=1;j<=m;j++) 41 { 42 if((j==1||s[j-1]=='0')&&s[j]=='1') id=j; 43 else if(j!=1&&s[j-1]=='1'&&s[j]=='0') t[++cnt].l=id,t[cnt].r=j-1,t[cnt].id=i; 44 if(s[j]=='1'&&j==m) t[++cnt].l=id,t[cnt].r=m,t[cnt].id=i; 45 } 46 } 47 sort(t+1,t+1+cnt,cmp3); 48 // int qz=0; 49 while(!q1.empty()) q1.pop(); 50 while(!q2.empty()) q2.pop(); 51 int nw=0; 52 bool ok=1; 53 memset(vis,0,sizeof(vis)); 54 for(int i=1;i<=m;i++) 55 { 56 int hh=0; 57 while(t[nw+1].l<=i&&nw<cnt) q1.push(t[++nw]); 58 while(!q2.empty()&&q2.top().r<i) {vis[q2.top().id]=0;q2.pop();} 59 while(q2.size()<k) 60 { 61 if(q1.empty()||q1.top().r<i) {ok=0;break;} 62 vis[q1.top().id]=1; 63 q2.push(q1.top());q1.pop(); 64 hh++; 65 if(hh>l&&i!=1) break; 66 } 67 if((hh>l&&i!=1)||!ok) {ok=0;break;} 68 while(hh<l&&!q1.empty()&&q1.top().r>q2.top().r) 69 { 70 hh++; 71 vis[q2.top().id]=0; 72 q2.pop(); 73 vis[q1.top().id]=1; 74 q2.push(q1.top());q1.pop(); 75 } 76 op[i][0]=0; 77 for(int j=1;j<=n;j++) if(vis[j]) op[i][++op[i][0]]=j; 78 } 79 if(!ok) printf("1 "); 80 else 81 { 82 for(int i=1;i<=m;i++) 83 { 84 for(int j=1;j<=op[i][0];j++) printf("%d ",op[i][j]); 85 printf(" "); 86 } 87 } 88 } 89 return 0; 90 }
2017-04-24 20:03:42
