4555: [Tjoi2016&Heoi2016]求和
Time Limit: 40 Sec Memory Limit: 128 MB
Submit: 315 Solved: 252Description
在2016年,佳媛姐姐刚刚学习了第二类斯特林数,非常开心。
现在他想计算这样一个函数的值:S(i, j)表示第二类斯特林数,递推公式为:S(i, j) = j ∗ S(i − 1, j) + S(i − 1, j − 1), 1 <= j <= i − 1。边界条件为:S(i, i) = 1(0 <= i), S(i, 0) = 0(1 <= i)你能帮帮他吗?Input
输入只有一个正整数
Output
输出f(n)。由于结果会很大,输出f(n)对998244353(7 × 17 × 223 + 1)取模的结果即可。1 ≤ n ≤ 100000
Sample Input
3Sample Output
87HINT
Source
【分析】
额。。要用第二类斯特林数的展开式?
表示并不会。于是看题解。ORZ。。ATP大神
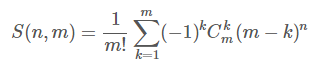
带进去,注意不用管j从1到i,因为j从1到n的话后面都是0,没有关系的。
最后化成

一脸卷积么?个人认为还不是很能看出来。
但是,就是!
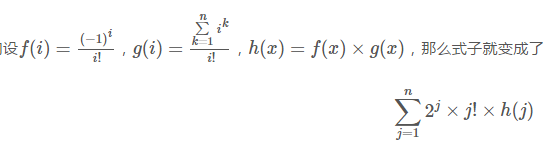
h用NTT求,然后求和即可。
再次ORZ。。

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 #define Maxn 500010 8 #define LL long long 9 const int Mod=998244353; 10 const int G=3; 11 12 int a[Maxn],b[Maxn],fac[Maxn]; 13 14 int qpow(int x,int b) 15 { 16 int ans=1; 17 while(b) 18 { 19 if(b&1) ans=1LL*ans*x%Mod; 20 x=1LL*x*x%Mod; 21 b>>=1; 22 } 23 return ans; 24 } 25 26 int nn,R[Maxn],inv; 27 void ntt(int *s,int f) 28 { 29 for(int i=0;i<nn;i++) if(i<R[i]) swap(s[i],s[R[i]]); 30 for(int i=1;i<nn;i<<=1) 31 { 32 int wn=qpow(G,(Mod-1)/(i<<1)); 33 for(int j=0;j<nn;j+=(i<<1)) 34 { 35 int w=1; 36 for(int k=0;k<i;k++) 37 { 38 int x=s[j+k],y=1LL*w*s[j+k+i]%Mod; 39 s[j+k]=(x+y)%Mod;s[j+k+i]=((x-y)%Mod+Mod)%Mod; 40 w=1LL*w*wn%Mod; 41 } 42 } 43 } 44 if(f==-1) 45 { 46 reverse(s+1,s+nn); 47 for(int i=0;i<=nn;i++) s[i]=1LL*s[i]*inv%Mod; 48 } 49 } 50 51 int main() 52 { 53 int n; 54 scanf("%d",&n); 55 fac[0]=1;for(int i=1;i<=n;i++) fac[i]=1LL*i*fac[i-1]%Mod; 56 for(int i=0;i<=n;i++) 57 { 58 a[i]=qpow(fac[i],Mod-2); 59 if(i&1) a[i]=Mod-a[i]; 60 b[i]=(1-qpow(i,n+1))%Mod; 61 b[i]=1LL*b[i]*qpow(1-i,Mod-2)%Mod; 62 b[i]=1LL*b[i]*qpow(fac[i],Mod-2)%Mod; 63 b[i]=(b[i]%Mod+Mod)%Mod; 64 } 65 nn=1;int ll=0; 66 while(nn<=2*n) nn<<=1,ll++; 67 for(int i=0;i<=nn;i++) R[i]=(R[i>>1]>>1)|((i&1)<<(ll-1)); 68 inv=qpow(nn,Mod-2); 69 b[1]=n+1; 70 ntt(a,1);ntt(b,1); 71 for(int i=0;i<=nn;i++) a[i]=1LL*a[i]*b[i]%Mod; 72 ntt(a,-1); 73 int ans=0; 74 for(int i=0;i<=n;i++) ans=(ans+1LL*a[i]*qpow(2,i)%Mod*fac[i])%Mod; 75 printf("%d ",ans); 76 return 0; 77 }
代码只需在FFT基础上修改一点点即可。
对于原根,因为你读题时就知道模数,你可以自己打个暴力求一下。具体方法在FFT和NTT总结中有说。
然后你直接赋值原根G的值就好了。
2017-04-14 15:10:42
