20220413模拟赛 总结
据说是 WC 2018 Day 1,直接考炸。。。
这次也许是失误最多的一场比赛。。。
T1 养花
题意
\(n\) 个数,第 \(i\) 个是 \(a_i\) ,每次询问 \(l,r\) 中 \(a_i\;mod\;k\) 的最大值
\(n,m,k\le 10^5\)
一波三折
考试时,5min 内,我打开了题目,一看题,WC,求 \(a_i\ \text{xor}\ k\) 最大,
这不裸的可持久化 trie 吗?
但我好像忘了。。。
哦没事,我记得思路,这种东西不就调试几下就出来了嘛。
- 0.5h 后
我去这样例是不是有问题啊,怎么过不了!
恩,则么是 \(a_i\;mod\;k\) 。
恩?
一阵 mmp 后我再次思考
想到了对于值域上形如 \([ak,(a+1)k]\) 的区间,最大值是最优的
暴力枚举这些区间?折腾了 0.5h 的各种做法,好像只有这样。
于是又打了一个莫队 + 值域分块,对于 \(k\) 比较大的情况能骗许多分。
是的,1.5h 过了,只打了一个暴力??
正解
确实是分块,但不是值域分块。
如考场思路,对于值域上形如 \([ak,(a+1)k]\) 的区间,最大值是最优的
考虑对原数组分块, \(mx_{i,k}\) 表示第 \(i\) 块中 \(\; mod\;k\) 的最大值
值域中,可以求出值 \(i\) 的前驱 \(ls_i\)
对于 \(k\) ,枚举所有形如 \([ak,(a+1)k]\) 的区间,取 \(\max\)
按普通分块的方法查询即可。
复杂度:
所有的 \(k\) ,形如 \([ak,(a+1)k]\) 的区间总数不超过 \(k\ln k\)
设块长为 \(L\) ,则预处理 \(\dfrac{n}{L}\times k\ln k\) ,查询 \(m\times(\dfrac{n}{L}+L)\)
要使与处理与查询尽量均衡,即 \(\dfrac{n}{L}\times k\ln k=m\times(\dfrac{n}{L}+L)\)
\(n,m\) 同阶,同乘 \(\dfrac{L}{n}\) 得 \(k\ln k=n+L^2\) ,所以 \(L=\sqrt{k\ln k}\approx 1000\) 时复杂度最优
code
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
const int N = 100005;
const int Bsz = 1000, SQ = 105;
int n, Ti, a[N], ls[N], po[N], pl[SQ], pr[SQ], Btot, mx[SQ][N];
int main() {
scanf("%d%d", &n, &Ti);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]), po[i] = (i - 1) / Bsz + 1;
Btot = po[n];
for (int i = 1; i <= Btot; i++) pl[i] = pr[i - 1] + 1, pr[i] = min(i * Bsz, n);
for (int i = 1; i <= po[n]; i++) {
memset(ls, 0, sizeof(ls));
for (int j = pl[i]; j <= pr[i]; j++) ls[a[j]] = a[j];
for (int j = 1; j <= 1e5; j++) ls[j] = max(ls[j], ls[j - 1]);
for (int j = 2; j <= 1e5; j++)
for (int k = 0; k <= 1e5; k += j) mx[i][j] = max(mx[i][j], ls[min(100000, k + j - 1)] - k);
}
for (int l, r, k, p, q, re; Ti--;) {
scanf("%d%d%d", &l, &r, &k);
if (k == 1) {
puts("0");
continue;
}
re = 0;
p = po[l], q = po[r];
if (p == q) {
for (int i = l; i <= r; i++) re = max(re, a[i] % k);
} else {
for (int i = l; i <= pr[p]; i++) re = max(re, a[i] % k);
for (int i = p + 1; i < q; i++) re = max(re, mx[i][k]);
for (int i = pl[q]; i <= r; i++) re = max(re, a[i] % k);
}
printf("%d\n", re);
}
}
T2 折射
题意
\(n\) 个点 ,折线从某个坐标出发,
依次经过若干点,经过 \(k\) 个点则必须满足
- \(\forall j\in(1,k],\quad y_j<y_{j-1}\)
- \(\forall j\in(2,k],\quad x_{j-2}<x_j<x_{j+1}\or x_{j-1}<x_j<x_{j-2}\)
求多少种不同线,\(\;mod\;10^9+7\)
波折 & 题解
考场按照 \(y\) 排序,直接卡在 \(O(n^3)\) ,凉凉
正解:
按照 \(x\) 排序,设 \(f_{i,0/1}\) 为当前到 \(i\) 点,折线往左 / 右射出时的方案(如图)
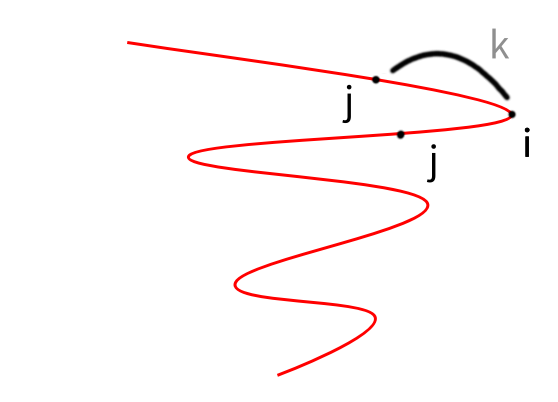
-
从 \(i\) 往左的从先前 \(j\) 向右的转移,即对于 \(y_j<y_i\) ,\(f_{i,0}\rightarrow f_{j,1}\)
-
从 \(i\) 往右,此时 \(i\) 还未向右射,需要从后面的点往左射来更新
所以,对于枚举到的 \(i\) ,我们用它去更新 \(j\) 的 \(f_{j,1}\) 。
即对于 \(y_j>y_i\) ,\(f_{j,1}\) 可以从所有的 \(k\in(j,i)\and x_k>x_i\and y_k<y_i\) 的 \(f_{k,0}\) 转移
这是是 \(O(n^3)\) 的,怎么办?
-
仔细研究条件,\(x_k>x_i\and y_k<y_i\) ,由于我们按 \(x\) 排了序,
直接倒叙枚举,\(f_{i,0}\) 即为所有 \(f_{k,0}\) 的和
答案为 \(\sum f_{i,0}+f_{i,1}\)
若初始化 \(f_{i,0}=f_{i,1}=1\) ,则答案要减去 \(n\)
code
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
const int N = 6005;
const LL P = 1e9 + 7;
int n;
LL f[N][2], ans;
struct mr {
int x, y;
} a[N];
inline bool cmp(mr A, mr B) {
if (A.x ^ B.x)
return A.x < B.x;
return A.y < B.y;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d%d", &a[i].x, &a[i].y);
sort(a + 1, a + n + 1, cmp);
for (int i = 1; i <= n; i++) {
f[i][0] = f[i][1] = 1;
for (int j = i - 1; j >= 1; j--) {
if (a[j].y < a[i].y)
(f[i][0] += f[j][1]) %= P;
if (a[j].y > a[i].y)
(f[j][1] += f[i][0]) %= P;
}
}
for (int i = 1; i <= n; i++) (ans += (f[i][0] + f[i][1]) % P) %= P;
printf("%lld", (ans + P - n) % P);
}
T3 画画
题意
\(n\times m\) 的 01 矩阵,初始全是 0,每一次可以将一个四连通部分全部涂成 0 或 1
问达到目标状态的最小次数
波折
理解错误:以为四连通就是上下左右加自己共 5 个点,
骗分打了一个 A* ,调了很久。
当我发现是连通块时,直接放弃
题解
结论题
结论:存在最优方案使得每次操作的区域是上一次的子集且颜色与上一次相反
感性理解
归纳证明:设 \(S\) 为当前所有操作区域的并, \(T\) 为接着这一步的操作区域,则
-
\(S\cap T\ne \varnothing\) 一定可以转为 \(T\) 被 \(S\) 包含
-
\(S\cap T=\varnothing\) 可以找一个连接 \(S\) 和 \(T\) 的集合 \(M\) 并操作 \(S\cup T\cup M\) ,
并将之前的所有操作连接到更外的层以及外层的连接部分同时操作, 特殊处理最外层和第二层的情况
-
\(T\) 被 \(S\) 包含,\(T\) 落在在某个完整区域内时等价于情况二,
否则一定连接若干个同色块, 这些块可以同时处理, 步数一定不会更劣
得知结论后,枚举最后被修改的区域,
答案就是将同色边边权当成 0,异色边权当成 1 后距离这个点最远的黑色点距离,对所有点取 \(\min\)
实现:这就是 01 bfs ,前几天才做过
code
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
const int N = 55, INF = 0x3f3f3f3f;
const int dx[5] = { 1, -1, 0, 0 }, dy[5] = { 0, 0, 1, -1 };
int n, m, dis[N][N], ans = INF, res, nx, ny;
char mp[N][N];
struct poi {
int x, y;
} nw;
deque<poi> Q;
inline int bfs(int sx, int sy) {
memset(dis, 0x3f, sizeof(dis));
dis[sx][sy] = 0;
Q.push_front((poi){ sx, sy });
res = 0;
while (!Q.empty()) {
nw = Q.front(), Q.pop_front();
nx = nw.x, ny = nw.y;
if (mp[nx][ny] == '1')
res = max(res, dis[nx][ny]);
for (int i = 0, xx, yy; i < 4; i++) {
xx = nx + dx[i], yy = ny + dy[i];
if (xx < 1 || xx > n || yy < 1 || yy > m || dis[xx][yy] < INF)
continue;
if (mp[xx][yy] == mp[nx][ny]) {
dis[xx][yy] = dis[nx][ny];
Q.push_front((poi){ xx, yy });
} else {
dis[xx][yy] = dis[nx][ny] + 1;
Q.push_back((poi){ xx, yy });
}
}
}
return res;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%s", mp[i] + 1);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) ans = min(ans, bfs(i, j));
printf("%d", ans + 1);
}
总结
-
T1 是对于 \(\ln k\) 这个预处理没有想到,同时也是没有数列分块
以后想分块从多角度,不死磕离线
-
T2 的排序是关键,排完序后的状态从后转移前面的思维很巧妙
-
(猜)结论,之后是01 bfs,一道偏数学的题