今天接到scy的压缩包,开始做数论专题。那今天就总结一下拓展欧几里得求解不定方程和同余方程组。
首先我们复习一下欧几里得算法:
1 int gcd(int a,int b){
2 if(b==0) return a;
3 return gcd(b,a%b);
4 }
拓展欧几里得算法:
推导过程:
给出A和B,求它们的最大公约数,并且求出x和y,满足Ax+By=gcd(A,B)。
当A=0时,x=0,y=1;
当A>0时,
因为exgcd(A,B,x,y)表示Ax+By=gcd(A,B)
而且exgcd(B%A,A,tx,ty)表示 B%A * tx + A*ty = gcd(B%A,A)
又gcd(A,B)== gcd(B%A,A),所以B%A * tx + A*ty ==Ax+By
方程:
![]()
![]()
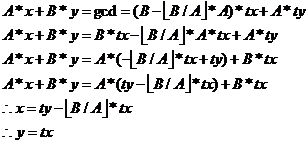
程序实现:
1 int tx,ty;
2
3 int exgcd(int a,int b)
4 {
5 if(b==0) {tx=1,ty=0;return a;}
6 int d=exgcd(b,a%b);
7 int x=ty,y=tx-(a/b)*ty;
8 tx=x;ty=y;
9 return d;
10 }
求解不定方程
已知a,b,n,求x,使得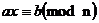 ,可以转化为:
,可以转化为: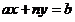 ,则要求gcd(a,n)|b,否则无解。
,则要求gcd(a,n)|b,否则无解。
poj2115--C Looooops
在另一篇博文 http://www.cnblogs.com/KonjakJuruo/p/5178503.html
poj1061 青蛙的约会
在另一篇博文 http://www.cnblogs.com/KonjakJuruo/p/5178505.html
中国剩余定理
从网上找到一段解释,觉得很好:
《孙子算经》中有“物不知数”问题:“今有物不知其数,三三数之余二 ,五五数之余三 ,七七数之余二,问物几何?”答为“23”。
--------这个就是传说中的“中国剩余定理”。 其实题目的意思就是,n % 3 = 2, n % 5 = 3, n % 7 = 2; 问n是多少?
那么他是怎么解决的呢?
看下面:
题目中涉及 3, 5,7三个互质的数、
令:5 * 7 * a % 3 = 1; --------------> a = 2; 即5 * 7 * 2 = 70;
3 * 7 * b % 5 = 1; --------------> b = 1; 即3 * 7 * 1 = 21;
3 * 5 * c % 7 = 1; --------------> c = 1; 即3 * 5 * 1 = 15;
为什么要使余数为1:是为了要求余数2的话,只要乘以2就可以,要求余数为3的话,只要乘以3就可以!
( 因为题目想要n % 3 =2, n % 5 =3, n % 7 =2; )
那么:要使得n % 3 = 2,那么( 5 * 7 * 2 )*2 % 3 = 2;( 因为5 * 7 * 2 % 3 = 1 )
同理: 要使得n % 5 = 3,那么( 3 * 7 * 1 )*3 % 5 = 3;( 因为3 * 7 * 1 % 5 = 1 )
同理:要使得n % 7 = 2,那么( 3 * 5 * 1 )* 2 % 7 = 2;( 因为3 * 5 * 1 % 7 = 1 )
那么现在将( 5 * 7 * 2 )* 2和( 3 * 7 * 1 )* 3和( 3 * 5 * 1 )* 2相加会怎么样呢?我们知道
( 5 * 7 * 2 )* 2可以被5和7整除,但是%3等于2
( 3 * 7 * 1 )* 3可以被3和7整除,但是%5等于3
( 3 * 5 * 1 )* 2可以被3和5整除,但是%7等于2
那么即使相加后,%3, 5, 7的情况也还是一样的!
那么就得到一个我们暂时需要的数( 5 * 7 * 2 )* 2 +( 3 * 7 * 1 )* 3 +( 3 * 5 * 1 )* 2 = 233
但不是最小的!所有我们还要 233 % ( 3 * 5 * 7 ) == 23 得解!
该解释来自博客http://blog.csdn.net/shanshanpt/article/details/8724769
注意:对于问题类似P%ai=bi(i=1 2 3 ……),中国剩余定理只能求解ai两两互质的情况。为什么?我们可以这样想,如果上面的例子改成%3 %5 %6,那么6*5*a就不可能满足%3=1的条件。
那么我今天和魔芋讨论的时候,想:为了满足条件,如果我分解质因数,乘的系数是除了公因数以外的因数相乘而得的乘积可以吗?后来讨论发现是不可以的,因为我们已经无法保证相加时不改变余数的条件了。
poj1006 biorhythms
http://www.cnblogs.com/KonjakJuruo/p/5178510.html
不互素怎么办?同余方程组
中国剩余定理求的同余方程组mod 的数是两两互素的。mod的数可能不是互素,所以要转换一下再求。
P=b1(mod a1); P / a1 ==?~~~~b1
P =b2(mod a2);
P =b3(mod a3);
……
P =bn(mod an);
a1~an,b1~bn是给出来的。
解:
第一条:a1*x+b1=P
第二条:a2*y+b2=P
第一条减去第二条: a1*x - a2*y = b2-b1
设A=a1,B=-a2,K=b2-b1,得到了x(实际调用exgcd的时候不理会a2前面的负号)
如果K%d!=0,无解
否则,X=[ (x* K/d)%(B/d)+(B/d) ]%(B/d)
LCU表示最小公倍数
P= a1*X+b1+ 若干倍的LCU(a1,a2)(或者把Y=(K-AX)/B,再P=a2*Y+b2+ 若干倍的LCU(a1,a2)
所以新的b= a1*x+b1,新的a= LCU(a1,a2),
把新的b当成b1,新的a当成a1,再去和a3和b3结合,一直到最后结束,最后新的b就是X
poj2891 Strange Way to Express Integers
http://www.cnblogs.com/KonjakJuruo/p/5178513.html
今天就学了这么些,要加油啊!