1. 参考论文
Reweighted Random Walks for Graph Matching【1】
The pagerank citation ranking: Bringing order to the web【2】
A spectral technique for correspondence problems using pairwise constraints【3】
2. 论文概述
论文提出了全新的思路——马尔科夫链去解决图匹配问题,提出了“基本版” Random Walk 并从随机游走角度恰好解释了【3】的谱方法SM的理论。随后根据【2】的思路改进成 RRM,通过实验证明其效果还是蛮不错的。
3. 论文介绍
3.1 传统问题描述
传统的图匹配问题,优化的目标函数为:
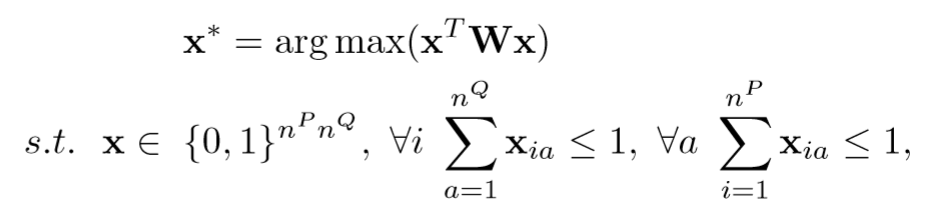
通过限制条件可以看出这是 IQP (integer quadratic program) 问题,其中 w 是两个图的相似度矩阵,x 是排列矩阵的列向量化(vec)
3.2 Markov角度问题描述
这是论文最核心的地方,即如何将传统的图匹配问转化为随机过程Markov的问题。我们先看平时场见的相似度矩阵 w 的形式:

观察上图(g),可以发现不管行、列,其坐标每一项代表含义都是两图中两个点的假设对应关系,如 1a 。我们最终的目的也是找到类似如此的对应关系,只不过这里借助的是相似度矩阵。
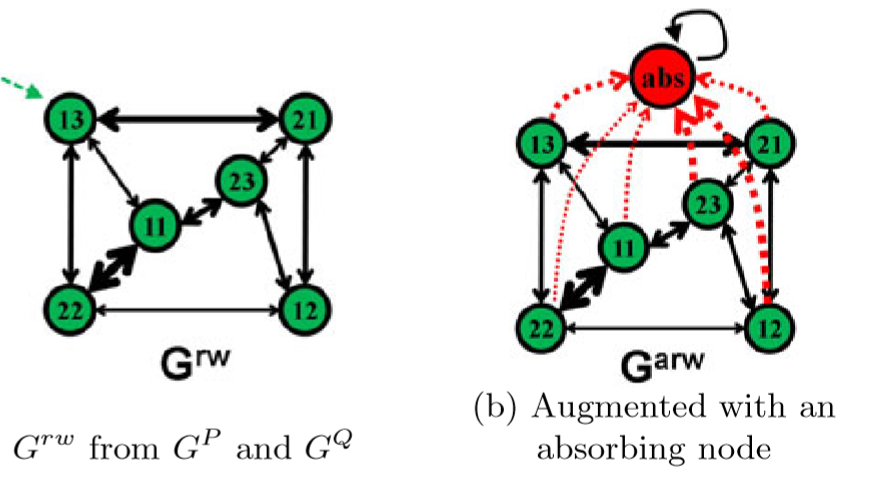
那么,作者就是从相似度矩阵出发,将其改造成随机游走模型,如图:

两个图P、Q的点的对应关系就当作Grw的结点,而相似度矩阵的对角线上的值(即一阶点的对应关系)当作Grw的 attribute,相似度矩阵非对角线上的 attribute 当作Grw的两个顶点(如13--22)构成的边的值。这样一来,我们将相似度矩阵就变换成了Grw的形式,同时,整个图匹配问题,变成了在改图上的随机游走过程,最终的目标成了在Grw上选点的过程—— To select the nodes in Grw( selecting reliable nodes in the Grw)
而如何选点,论文借鉴了【2】.
3.3 转移矩阵
Markov 过程需要一个转移矩阵(概率矩阵),那么对应到这里,怎么构建呢?首先可以明确的是,肯定是从 w 入手,将其改造成转移矩阵——每行和为1,每一项 ≥ 0(满足)。
对于前者条件,一种常见的思路是:
即求 w 每一行的和,然后改行分别处以该数——但是其弊处明显,文中提到这种做法会放大不匹配点的概率,即相似度矩阵本来是相似度值的大小,通过除法,会削弱相似度大的值,反之放大原本小的值的匹配概率(如 1 0 2;3 0 6;---->均为 1/3 0 2/3)
作者采用将 w 矩阵每一项均除以 max(sum(和)),即以此做法保护原来相似度值较大的点。思路是这样,然后为了满足Markov的sum(行)=1的特点,需要改造转移矩阵:

其中左式 P 就是转移矩阵,其中dmax = max(sum(行和)),d(向量)是每行和,式子第一项就是为了满足转移矩阵行和为1,同时底部第二行是为了保证P是个方阵,原本是 xP,既然 P 是多了一项,所以改造x,引入(x xabs)P,即如上图右边式子,上标n代表转移次数
而引入 xabs,其实就是对Grw再此进行改造,增加一个虚拟结点(absorb 吸收点),因为 P 的转移概率是(0000....000 1), 即恰好代表 nm*nm+1 这个结点不会转移到其他点,只能自转移,概率为1。
如下图,就是引入该 abs 的图
3.4 为什么求解Markov链的稳态就是结果
论文最终就是通过 P 转移矩阵,求得 x 的稳态(稳态Markov链),我想因为 x 的初始分布(应该)可以平均分配(即随机游走开始(1/mn*mn 1/mn*mn.....)),而Grw的edge代表了相似度,进一步该相似度被转化成了P(即概率表示),那么最终得到的 x 的值(再还原回矩阵)代表了两两结点如何匹配的score,然后使用匈牙利算法即可选出该x还原回来的矩阵的最佳匹配score
至于为什么稳态(转移矩阵n次幂)一定存在:

但是如果按上述设计转移矩阵 P,其最终的迭代结果是 (00000....000 1),所以如果迭代到一定次数即可,得到近似解
3.5 RM与SM效果的一致性证明
作者提到,RM 是从随机游走角度解释了谱方法【2】的做法(即选取 w 的最大特征值),证明如下:
首先引入一个概率分布

其中 X^(n) 是随机变量表示(2)转移公式中节点在n时刻的位置,x(hat)ia(n) 是如上定义的概率,表示为游走到absorb node 点的条件概率。同时记
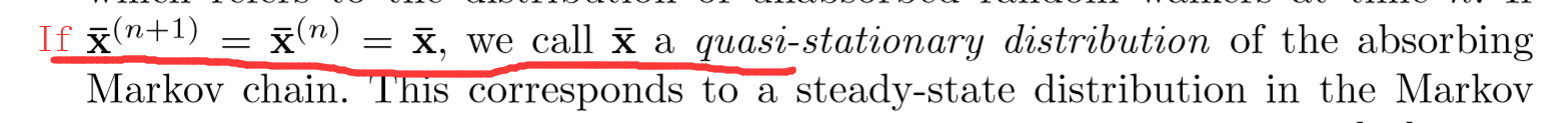
同时给出定义、定理:
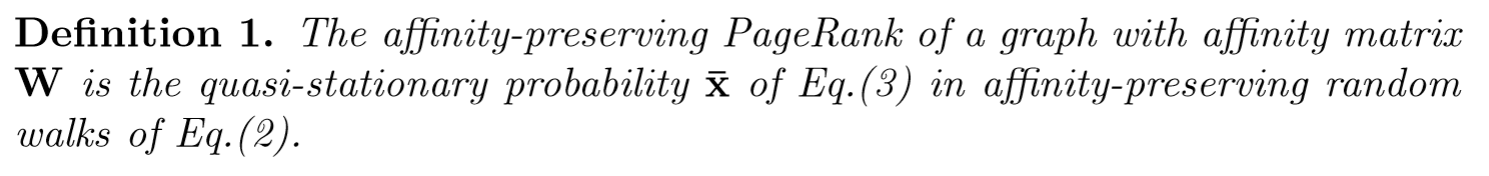


然后
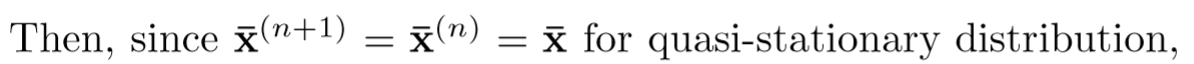
这里一定要注意,个人觉得,按照上述P的转移矩阵, XP---XPP----XPPP..... 最后X 一定变成了(0000 1),前面提过这点。所以这里 xhat(n) 表示的是条件概率,即不是以任意点开始游走,然后均以 absorb node 点为最终结果的的概率,也就是没有算到最后稳态(迭代到稳态之前停止),那么
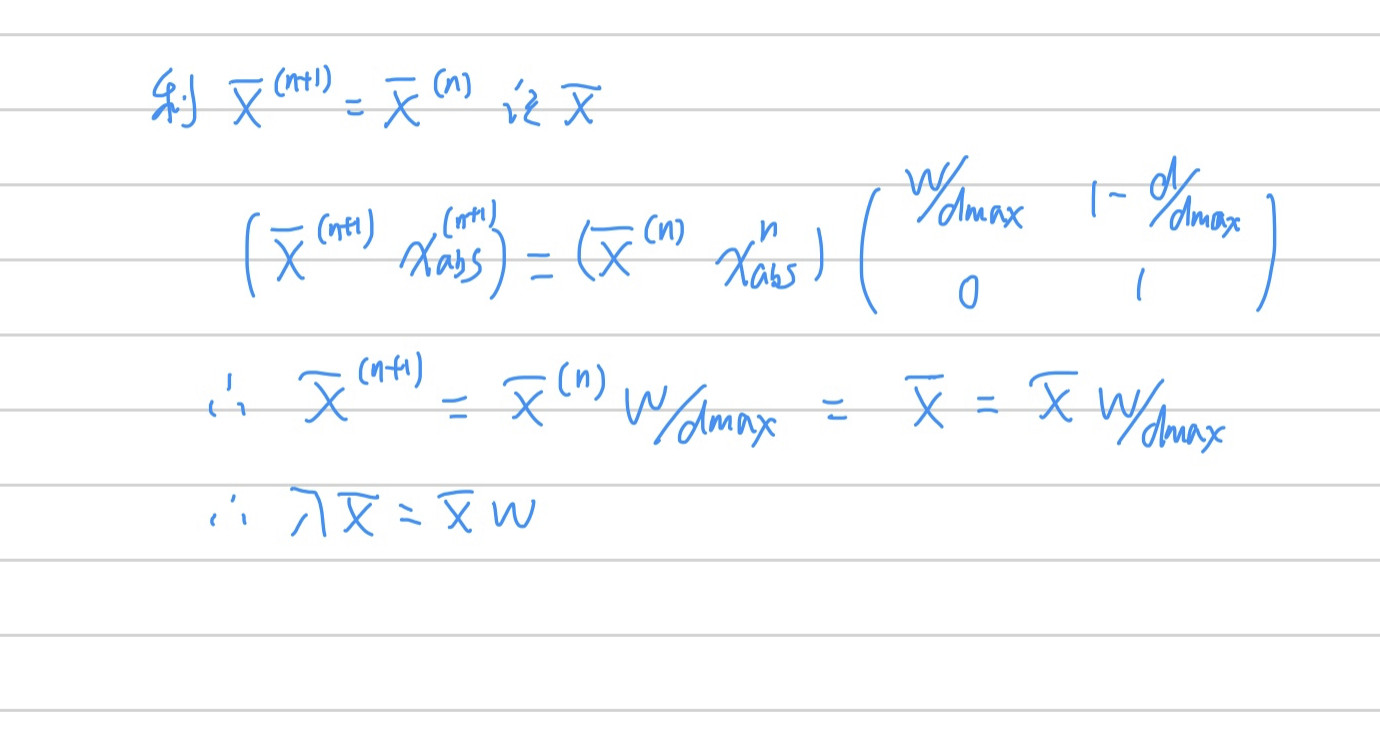
根据 Perron Frobenius theorem,① w 是不可约的 ② x hat 是非负的,则上述 “lamda” 是最大左特征值,对应的 x hat 是特征向量。
而这正好同SM【3】观点相同,得到近似解,则只要求 w 的最大特征向量,随后矩阵化得到排列矩阵
3.6 Reweighted Random Walk
通过RW,已经达到了SM的效果,更进一步,作者还是根据【2】的思路设计了RRW——作者给出的RW的不足的解释是IQP的subject限制条件未在Markov中体现(这里我不理解,是≤1这个条件未满足?我觉得RRW最大的好处就是inflation,①在游走的时候让相似度大的点得到更到的被选概率②jump的存在提供了游走的更多状态空间,详见下) :

RRW就是改造转移概率,提出 personalization jump,即在Grw中可以选择①按照现有的边走下一步②也可以直接jump到其点
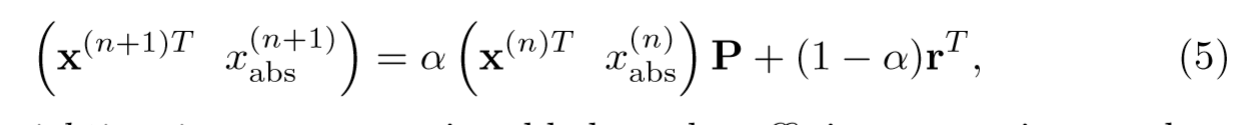
阿尔法就是选择继续按边walk 还是 1-α 选择jump。其中 r 是 reweighting jump vector 。
关于 r 的设计,一种方法是:直接使用当前的 x ,弊端是会让错误匹配(相似度点较小)的点不能在初期的迭代中排除掉。作者设计 r 从两个角度:① inflation ② bistochastic normalization。后者是归一化成双随机矩阵。
前者使用这样一个公式: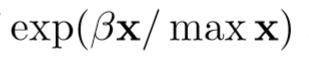 ,用意是:
,用意是:
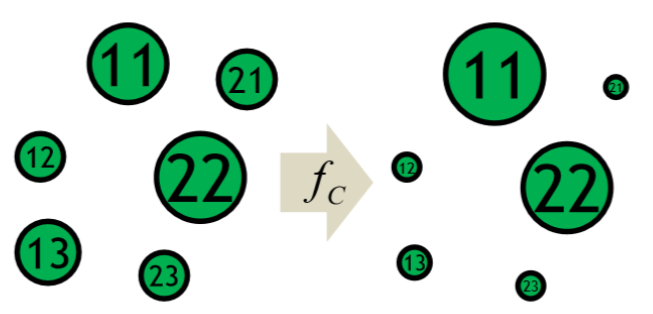
Strong candidates are amplified while weak candidates are attenuated。
所以最终:

其中 fc函数就是实现 inflation 和 bistochastic normalization的
3.7 RRW Algorithm

最后得到的 x 是个矩阵score,类似如下:
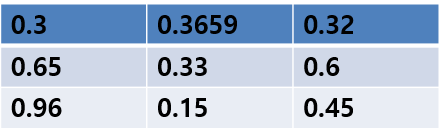
通过匈牙利算法可以得到选择行列匹配关系是score最大的。匈牙利算法