SHOI2015 超能粒子炮·改

求

$S_n^k = sum_{i=0}^k C_n^i$ 膜 $2333$

Lucas 定理的高端操作 学习了

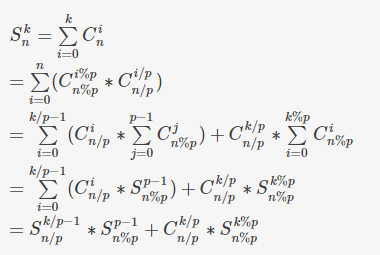
#include<bits/stdc++.h>
#define LL long long
using namespace std;
inline int read()
{
    int x = 0,f = 1;char ch = getchar();
    for(;!isdigit(ch);ch = getchar())if(ch == '-')f = -f;
    for(;isdigit(ch);ch = getchar())x = 10 * x + ch - '0';
    return x * f;
}

const int mod=2333;

int c[mod+1][mod+1],sum[mod+1][mod+1];

LL lucas(LL n,LL k)
{
    if(n<k||k<0)return 0;
    if(n<mod&&k<mod)return c[n][k];
    return lucas(n/mod,k/mod)*c[n%mod][k%mod]%mod;
}

LL cal(LL n,LL k)
{
    if(k<0)return 0;
    return (cal(n/mod,k/mod-1)*sum[n%mod][mod-1]+lucas(n/mod,k/mod)*sum[n%mod][k%mod])%mod;
}

int main()
{
    c[0][0]=sum[0][0]=1;
    for(int i=1;i<=mod;i++)
        sum[0][i]=1;
    for(int i=1;i<=mod;i++)
    {
        c[i][0]=sum[i][0]=1;
        for(int j=1;j<=i;j++)
            c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod,sum[i][j]=(sum[i][j-1]+c[i][j])%mod;
        for(int j=i+1;j<=mod;j++)
            sum[i][j]=sum[i][j-1];
    }
    int T;
    scanf("%d",&T);
    while(T--)
    {
        LL n,k;
        scanf("%lld%lld",&n,&k);
        printf("%lld
",cal(n,k));
    }
}