【前向星】链式前向星实现以及它的遍历

深度理解链式前向星

链式前向星的构成由一个结构体（包括目标点、边权值和下一个同起点的边）和head数组（用于存放某点的第一条出边）

必要的时候还可以添加一个统计入度的数组，因为进行BFS DFS的时候是依靠点的出度和出边的邻接关系来进行的。假如有多于一个点的入度为0，那么将只能遍历到其中一个点以及往后的内容。

对于链式前向星：链式前向星每添加一条边就会更新head数组，使得head数组存放的总是最新添加的某点的出边，此出边的next总指向head数组之前存放的出边的序号。

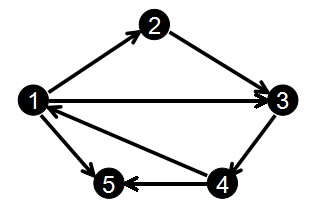
我们输入边的顺序为:

1 2

2 3

3 4

1 3

4 1

1 5

4 5

我们建立边结构体为:

struct Edge
{
     int next;
     int to;
     int w;
};

其中edge[i].to表示第i条边的终点

edge[i].next表示与第i条边同起点的下一条边的存储位置

edge[i].w为边权值

另外还有一个数组head[],它是用来表示以i为起点的新边存储的位置

实际上你会发现这里的新边存储的位置其实在以i为起点的所有边的最后输入的那个编号

head[]数组一般初始化为-1,对于加边的add函数是这样的:

void add(int u,int v,int w)  
{  
    edge[cnt].w = w;  
    edge[cnt].to = v;  
    edge[cnt].next = head[u];  
    head[u] = cnt++;  
}  

初始化cnt = 0,这样,现在我们还是按照上面的图和输入来模拟一下:

edge[0].to = 2;     edge[0].next = -1;      head[1] = 0;

edge[1].to = 3;     edge[1].next = -1;      head[2] = 1;

edge[2].to = 4;     edge[2],next = -1;      head[3] = 2;

edge[3].to = 3;     edge[3].next = 0;       head[1] = 3;

edge[4].to = 1;     edge[4].next = -1;      head[4] = 4;

edge[5].to = 5;     edge[5].next = 3;       head[1] = 5;

edge[6].to = 5;     edge[6].next = 4;       head[4] = 6;

很明显,head[i]保存的是以i为起点的所有边中编号最大的那个,而把这个当作顶点i的第一条起始边的位置.

这样在遍历时是倒着遍历的,也就是说与输入顺序是相反的,不过这样不影响结果的正确性.

比如以上图为例,以节点1为起点的边有3条,它们的编号分别是0,3,5   而head[1] = 5

我们在遍历以u节点为起始位置的所有边的时候是这样的:

for(int i=head[u];~i;i=edge[i].next)

那么就是说先遍历编号为5的边,也就是head[1],然后就是edge[5].next,也就是编号3的边,然后继续edge[3].next,也

就是编号0的边,可以看出是逆序的.

走进链式前向星的秘密      ←以上内容在这篇文章中用很简洁的语言解释了一遍

使用模板：

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define mae 10010 // 最大边数
#define mav 110   // 最大顶点数
using namespace std;

struct EdgeNode
{
    int v;
    int w;
    int next;
} g[mae];

int head[mae];
int t = 1;//edgenum 作用
int n, m;

bool visdfs[mav];
bool visbfs[mav];
void init()    //初始化
{
    memset(head, 0, sizeof(head));
    memset(visbfs, 0, sizeof(visbfs));
    memset(visdfs, 0, sizeof(visdfs));
    t = 1;
}

void add(int a, int b, int c) //加边
{
    g[t].v = b;  //当年节点 a指向b
    g[t].w = c;   // a->b 边的权值是 c
    g[t].next = head[a];  // next指向 上一条以a为起点的边
    head[a] = t;  //head[a] 表示以a为起点的最后输入的边的 编号
    t++;          // 给每一条以构建的边 制定编号（edgenum）
}

void Print()
{
    int k, i;
    for(i = 1; i <= n; i++)
    {
        if(head[i])//找边
        {
            for(k = head[i]; k != 0; k = g[k].next)
            {
                printf("%d->%d %d
", i, g[k].v, g[k].w);
            }
        }
    }
}

void DFS(int x)
{
    visdfs[x] = true;
    printf("%d
", x);
    for(int i = head[x]; i != 0; i = g[i].next)
    {
        if(!visdfs[g[i].v])
        {
            DFS(g[i].v);
        }
    }

}

void BFS(int x)
{
    int q[mav];//队列
    int jin = 0, chu = 0, st;
    q[jin++] = x;
    visbfs[x] = true;//标记
    while(chu < jin)
    {
        st = q[chu++];
        printf("%d
", st);
        for(int k = head[st]; k != 0; k = g[k].next)
        {
            if(!visbfs[g[k].v])
            {
                visbfs[g[k].v] = true; //标记
                q[jin++] = g[k].v;
            }
        }
    }
}

int main()
{
    int U, V, W, in;
    while(~scanf("%d%d", &n, &m))
    {
        init();
        for(int i = 1; i <= m; i++)
        {
            scanf("%d%d%d", &U, &V, &W);
            add(U, V, W);
        }
        in = 1;//此处以1为例开始搜索
        puts("建图为");
        Print();
        puts("dfs访问结果:");
        DFS(in);
        printf("-----------
");
        puts("bfs访问结果:");
        BFS(in);
    }
    return 0;
}

参考博客：

建图方式一 之 ”前向星“ BFS&&DFS 简单应用

链式前向星实现以及它的遍历

深度理解链式前向星