试题 G: 积木画
【问题描述】 小明最近迷上了积木画，有这么两种类型的积木，分别为 I 型（大小为 2 个单位面积）和 L 型（大小为 3 个单位面积）：
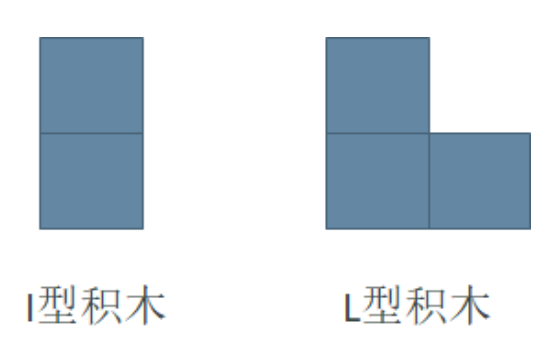
同时，小明有一块面积大小为 2 × N 的画布，画布由 2 × N 个 1 × 1 区域构成。小明需要用以上两种积木将画布拼满，他想知道总共有多少种不同的方式？ 积木可以任意旋转，且画布的方向固定。
【输入格式】 输入一个整数 N，表示画布大小。
【输出格式】 输出一个整数表示答案。由于答案可能很大，所以输出其对 1000000007 取 模后的值
【样例输入】 3
【样例输出】 5
【样例说明】 五种情况如下图所示，颜色只是为了标识不同的积木：
【评测用例规模与约定】 对于所有测试用例，1 ≤ N ≤ 10000000.
用 f[i] 表示i列的方法总数
接下来把状态分一下类
1. 第 i-1列已经排满的基础上,如图,方法数等于f[i-1]
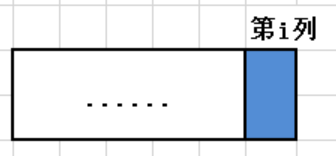
2.若第 i-1列没排任何积木(即与第i列构成如下图),方法数等于f[i-2]
3.
①若第 i-1列排了一半,只有如下两种情况, 方法数等于2*f[i-3]
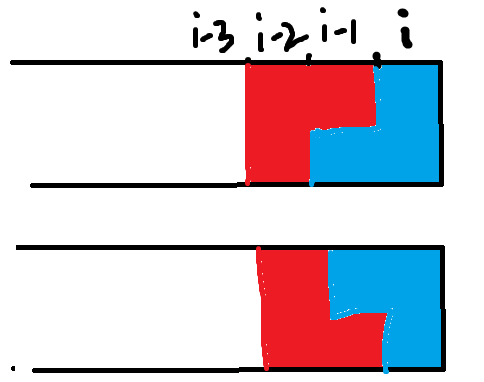
②上面的情况并不全面, 我发现第i-3置身事外
那用不用考虑下面这种情况呢, 明显是不用的,与上面情况2重复,
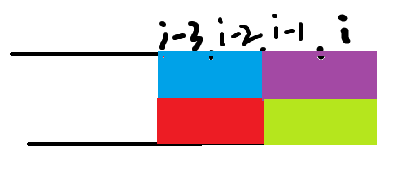
新的情况已经出现!, 方法数等于2*f[i-3]
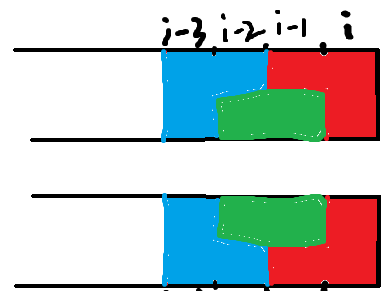
③这次把第i-4列拉下水, 这也是我们未曾考虑到的情况, 2*f[i-4]
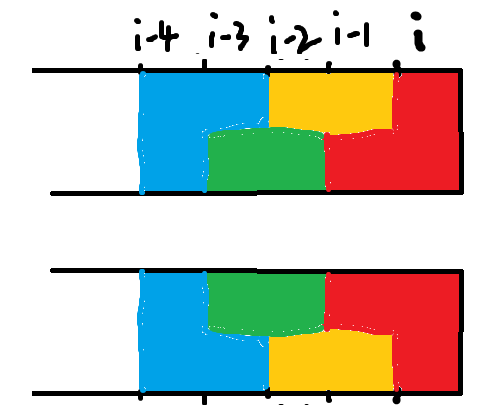
综上, 大胆假设出:
(o゜▽゜)o☆[BINGO!]
可以看出 f[1] = 1, f[2] = 2, f[3] = 5 ,剩下的递推即可
我的代码:
#include<iostream>
using namespace std;
const int N = 1e7+10, MOD = 1000000007;
int f[N];
int main()
{
f[1] = 1;
f[2] = 2;
f[3] = 5;
int n;
cin >> n;
for(int i = 4; i <= n; i ++)
{
f[i] = (2*f[i-1]%MOD+f[i-3]%MOD)%MOD;
}
cout << f[n];
return 0;
}据说是洛谷原题, 可惜没做过, 但幸好自己推出来了
P1990 覆盖墙壁 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
https://www.luogu.com.cn/problem/P1990