Codeforces Round #503 (by SIS, Div. 2)

A - New Building for SIS

题意：英语阅读，ab之间都有通道。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

void test_case() {
    int n, h, a, b, q;
    scanf("%d%d%d%d%d", &n, &h, &a, &b, &q);
    while(q--) {
        int t1, h1, t2, h2;
        scanf("%d%d%d%d", &t1, &h1, &t2, &h2);
        if(t1 == t2)
            printf("%d
", abs(h1 - h2));
        else if(a <= h1 && h1 <= b || a <= h2 && h2 <= b)
            printf("%d
", abs(h1 - h2) + abs(t1 - t2));
        else
            printf("%d
", min(abs(h1 - a) + abs(h2 - a), abs(h1 - b) + abs(h2 - b)) + abs(t1 - t2));
    }
}

int main() {
#ifdef KisekiPurin
    freopen("KisekiPurin.in", "r", stdin);
#endif // KisekiPurin
    int t = 1;
    for(int ti = 1; ti <= t; ++ti) {
        //printf("Case #%d: ", ti);
        test_case();
    }
}

B - Badge

题意：给一个内向基环树，求从每个点出发所走到的第一个被遍历两次的点。

题解：那肯定是环的入口，数据量太小可以直接暴力。但是假如变大的话：每个点记录入度，从每个入度为0的点出发，走到第一个计数2次的位置则发现了环，然后返回（错误，这样有可能会走到分叉，正确的是继承这个分叉点的信息）。假如没有入度为0的点，则剩下的点全是纯粹的环。在链上的点返回其在环的入口，在环上的点返回它本身。

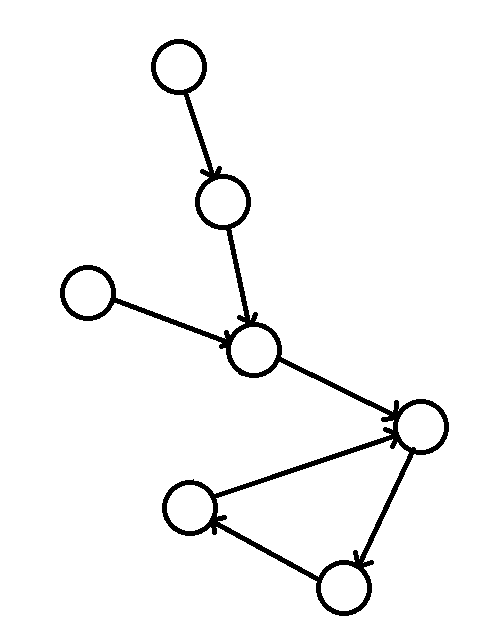
像这样的图，基环树的不是“链”而是“树”，这个要记住！

这样就不需要入度了，每次继承下一个点的就可以了。（原本入度的引入是为了区分“链”的末端和环上点，但事实上因为是“树”，所以必须从父节点继承，就导致入度没有必要了（不需要回溯时更新））

设计了一种基环树的dfs，就是每次染色，发现将要染的色是同色则发现了环，把环的入口标记然后回溯，直到遇到环的入口为止把回溯经过的节点全部标记为环，遇到环的入口后把经过的节点标记为环的入口。经过改动之后还可以传递更多信息，比如到达环的最短距离。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

int G[1005];
int vis[1005], col[1005], ans[1005];

int state;
void dfs(int u, int p, int c) {
    if(vis[u] == 1) {
        state = (col[u] == c) ? u : -ans[u];
        return;
    }
    vis[u] = 1, col[u] = c;
    dfs(G[u], u, c);
    ans[u] = (state > 0) ? u : -state;
    if(u == state)
        state = -u;
}

void test_case() {
    int n;
    scanf("%d", &n);
    for(int i = 1, j; i <= n; ++i) {
        scanf("%d", &j);
        G[i] = j;
    }

    for(int i = 1; i <= n; ++i) {
        if(!vis[i]) {
            dfs(i, -1, i);
            state = 0;
        }
    }

    for(int i = 1; i <= n; ++i)
        printf("%d%c", ans[i], " 
"[i == n]);
}

int main() {
#ifdef KisekiPurin
    freopen("KisekiPurin.in", "r", stdin);
#endif // KisekiPurin
    int t = 1;
    for(int ti = 1; ti <= t; ++ti) {
        //printf("Case #%d: ", ti);
        test_case();
    }
}

C - Elections

题意：要选举，有n个人m种派别，每个人有默认派别和huilu他需要的钱数，求使1号派别严格大于其他派别的最小钱。

题解：看见什么？最小钱？以为要二分？但是你是先huilu便宜的还是huilu比你高的派的呢？考虑到其实m<=3000，假设我们枚举x：除1号派以外的各个派的最大人数，然后把超过这个人数的最便宜的那堆拿走（这个可以大到小排序之后求后缀，然后越界返回0），这个是个可行的解法吗？在x过高的时候并不是，因为在x过高的时候要保证把1号派的堆到x+1，这样修补之后貌似就看起来正确多了。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

vector<int> G[3005];
vector<ll> suffix[3005];
vector<int> tmp;

void test_case() {
    int n, m;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; ++i) {
        int p, c;
        scanf("%d%d", &p, &c);
        G[p].push_back(c);
    }

    for(int i = 2; i <= m; ++i) {
        sort(G[i].begin(), G[i].end(), greater<int>());
        suffix[i].resize(G[i].size() + 1);
        for(int j = G[i].size() - 1; j >= 0; --j)
            suffix[i][j] = suffix[i][j + 1] + G[i][j];
    }

    ll ans = 1e18;
    for(int x = 0; x < n; ++x) {
        ll cost = 0;
        int cnt1 = G[1].size();
        for(int i = 2; i <= m; ++i) {
            if(G[i].size() > x) {
                cost += suffix[i][x];
                cnt1 += G[i].size() - x;
            }
        }
        if(cnt1 > x)
            ans = min(ans, cost);
        else {
            tmp.clear();
            for(int i = 2; i <= m; ++i) {
                int c = min((int)G[i].size(), x);
                for(int j = 0; j < c; ++j)
                    tmp.push_back(G[i][j]);
            }
            sort(tmp.begin(), tmp.end());
            int j = 0, c = tmp.size();
            while(j < c && cnt1 <= x) {
                ++cnt1;
                cost += tmp[j++];
            }
            if(cnt1 > x)
                ans = min(ans, cost);
        }
    }

    printf("%lld
", ans);
}

int main() {
#ifdef KisekiPurin
    freopen("KisekiPurin.in", "r", stdin);
#endif // KisekiPurin
    int t = 1;
    for(int ti = 1; ti <= t; ++ti) {
        //printf("Case #%d: ", ti);
        test_case();
    }
}

复杂度是nmlogn，这有个鬼办法哦。假如预处理每个x中每个派别的后缀，然后后面的贪心使用平衡树（nlogn），可能渐进复杂度会好看一点，但应该不会更快。