转载请注明出处:http://www.cnblogs.com/KirisameMarisa/p/4187670.html
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3306
Another kind of Fibonacci
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1720 Accepted Submission(s): 667
说简单点就是要求S(n)=∑f(n)2,其中f(n)=x*f(n-1)+y*f(n-2),且f(0)=1,f(1)=1。
首先,我们看到有f(n)=x*f(n-1)+y*f(n-2)这个式子,我想大家的第一反应一定是觉得很像斐波那契数列数列。没错,所以,再解这道题目之前,我们先来讲讲斐波那契数列的解法。
一、斐波那契数列的解法
斐波那契数列,又称黄金分割数列,指的是这样一个数列:1、1、2、3、5、8、13、21、……
在数学上,斐波纳契数列以如下被以递归的方法定义:F(0)=0,F(1)=1,Fn=F(n-1)+F(n-2)(n>=2,n∈N*)
二逼青年做法:显然可以逐项计算F(n),可以在O(n)的时间内得出答案,不过这种算法的效率太低了,一旦n是一个比较大的数必定超时无疑。
文艺青年做法:接着,数学系的同学可能第一反应就是求通项公式以期在O(1)的时间就可以得出答案。不错,斐波那契数列的通项公式是可以求的,前人已经求出来了:
但是在这个式子中有无理数出现,在计算机中使用浮点数是无法精确存储的,更加无法获得模某个数以后的结果,况且像斐波那契数列正好可以求到通项公式,别的就比如本题只能望洋兴叹了。
高端大气上档次狂拽酷炫吊炸天的计算机系有为青年做法(pia~拍飞):好了,言归正传,我们来看看真正在ACM程序设计竞赛中的做法。
矩阵是一个好东西,有时候我们可以利用矩阵来简化计算。我们可以把斐波那契数列的递推式变成矩阵形式,即构造一个矩阵:
记这个矩阵为A,则有:
所以,我们只要求出An就可以得到Fn了,如何快速求解An,那就要用到矩阵快速幂了,可以在O(logn)时间内求解,再次不细讲,大家可以看最终的代码实现。
二、类似斐波那契数列的求法
回到本题中,观察到有f(n)=x*f(n-1)+y*f(n-2)这样一个式子,我们想利用矩阵快速幂简化运算。不过在本题中我们遇到这样一个问题,尽管有了斐波那契数列的基础f(n)是很好求,但是要求∑f(n)就不行了,因为矩阵快速幂运算是“跳”着来的,跟别谈求∑f(n)2了。这时候,我们就要拓展一下思路了。
进一步推导递推式:S(n) = ∑f(n)2 = S(n-1)+f(n)2 = S(n-1)+x2f(n-1)2+y2f(n-2)2+2xyf(n-1)f(n-2)
其他都好办,就是有一项2xyf(n-1)f(n-2)比较讨厌,那么我们就继续进一步,再写一项:f(n)*f(n-1) = (x*f(n-1)+y*f(n-2))*f(n-1) = x*f(n-1)2+y*f(n-1)*f(n-2),这样就方便构造矩阵递推了。
我们构造矩阵递推式:
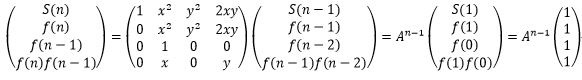
这样我们就能用上矩阵快速幂了,最后只要将An-1的第一行加起来就行了
#include <iostream> #include <ios> #include <iomanip> #include <functional> #include <algorithm> #include <vector> #include <sstream> #include <list> #include <queue> #include <deque> #include <stack> #include <string> #include <set> #include <map> #include <cstdio> #include <cstdlib> #include <cctype> #include <cmath> #include <cstring> #include <climits> using namespace std; #define XINF INT_MAX #define INF 1<<30 #define MAXN 0x7fffffff #define eps 1e-8 #define zero(a) fabs(a)<eps #define sqr(a) ((a)*(a)) #define MP(X,Y) make_pair(X,Y) #define PB(X) push_back(X) #define PF(X) push_front(X) #define REP(X,N) for(int X=0;X<N;X++) #define REP2(X,L,R) for(int X=L;X<=R;X++) #define DEP(X,R,L) for(int X=R;X>=L;X--) #define CLR(A,X) memset(A,X,sizeof(A)) #define IT iterator #define PI acos(-1.0) #define test puts("OK"); #define _ ios_base::sync_with_stdio(0);cin.tie(0); typedef long long ll; typedef pair<int,int> PII; typedef priority_queue<int,vector<int>,greater<int> > PQI; typedef vector<PII> VII; typedef vector<int> VI; #define X first #define Y second #define MOD 10007 typedef struct { int data[4][4]; } M; M I={1,0,0,0, 0,1,0,0, 0,0,1,0, 0,0,0,1}; M matrixmul(M a,M b) { M res=I; REP(i,4) { REP(j,4) { int temp=0; REP(k,4) temp=(temp+(a.data[i][k]*b.data[k][j])%MOD)%MOD; res.data[i][j]=temp; } } return res; } int pow_mod(M a,int n) { M res=I; while(n>0) { if(n&1) res=matrixmul(res,a); a=matrixmul(a,a); n>>=1; } int ans=0; REP(j,4) ans=(ans+res.data[0][j])%MOD; return ans; } int main() {_ int n,x,y; while(scanf("%d%d%d",&n,&x,&y)!=EOF) { x=x%MOD;y=y%MOD; M a={1,(x*x)%MOD,(y*y)%MOD,(2*x*y)%MOD, 0,(x*x)%MOD,(y*y)%MOD,(2*x*y)%MOD, 0,1,0,0, 0,x,0,y}; printf("%d\n",(pow_mod(a,n-1)+1)%MOD); } return 0; }
三、推广(《挑战程序设计竞赛 第二版》P201)
一般地,对于m项递推式,如果记递推式为

则可以把递推式写成如下矩阵形式
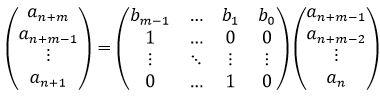
通过计算这个矩阵的n次幂,就可以在O(m3logn)的时间内计算出第n项的值。不过,如果递推式里面含有常数项则稍微复杂一些,需变成如下形式:

by--Kirisame_Marisa 2014-12-27 00:25:05
