题意:给一个如图坐标系,每个方形都放在下面两个中间,已知一个木块湿了那么他下面所有的都会湿,显然,不能湿两次。问,每次给出一个坐标,把他弄湿,有几个木块从干变成湿了。
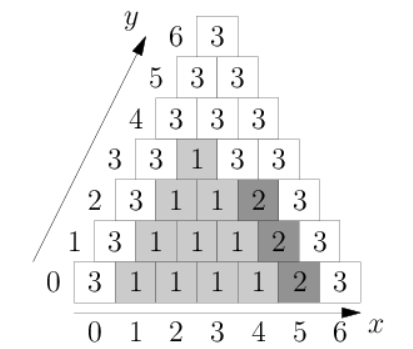
思路:我们把坐标系拉直,就变成了如图,显然我们弄湿 a(0,5),那么红色部分变湿,看一眼应该已经找到计算面积的方法了。所以我们每次得到一个坐标,我们就能直接算出面积。然后我们判断,是否已经有顶点所产生的面积包含了我的顶点,是的话我湿的面积为0。没有的话我就遍历一遍所有顶点,删掉所有的已经湿了的面积,剩下的就是新湿的面积了。
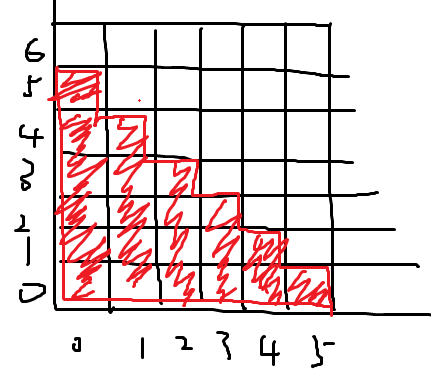
然后我们看一下,如果两个面积不相交,那么必有下图这样,我们可以简单的算出,红色最右边的x应该为a.x + a.y,那么不相交的条件为a.x + a.y < b.x。
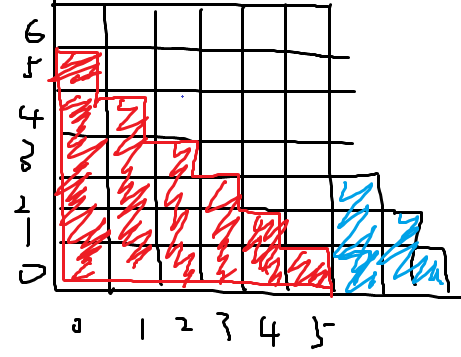
相含的时候,被包含的那个面积必然是从包含的面积内部一点为顶点,而红色内部所有的点都有一个性质x + y <= a.x + a.y && x >= a.x,所以以此判断包含关系。
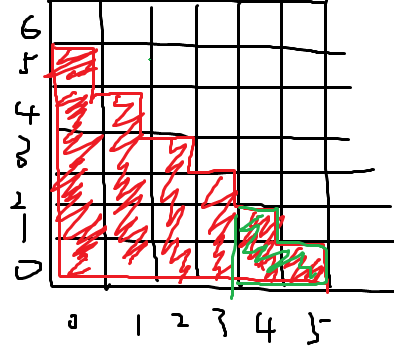
然后计算交集:显然交集为蓝色减去它内部小红色的面积。那么我们先判断是否有内含,有的话就是被含的面积;否则我们找出红色小面积的顶点,因为我们知道y的长度就可以算出面积,那么Y = a.x + a.y - b.x。

但是我们直接减去相交面积显然不行,因为可能有很多重复的面积被我减掉了。那怎么办?直接计算每次多减的加回去,多算的面积是两两之间的交集,一直加到最后一块和我相交的(也就是x >= a.x且不内含的第一块)。
代码:
#include<cmath> #include<set> #include<map> #include<queue> #include<cstdio> #include<vector> #include<cstring> #include <iostream> #include<algorithm> #include<unordered_map> using namespace std; typedef long long ll; typedef unsigned long long ull; const int maxn = 1e5 + 10; const int M = maxn * 30; const ull seed = 131; const int INF = 0x3f3f3f3f; const int MOD = 1e4 + 7; struct Tri{ ll x, y; bool operator < (const Tri a) const{ return x < a.x; } }; set<Tri> s; ll getAera(Tri a){ return (1LL + a.y) * (a.y + 2LL) / 2LL; } bool contain(Tri a, Tri b){ //a包含b return a.x + a.y >= b.x + b.y && a.x <= b.x; } ll intersect(Tri a, Tri b){ //a b交集 if(contain(a, b)) return getAera(b); else if(contain(b, a)) return getAera(a); else{ ll y = -1; if(a.x <= b.x) y = max(y, a.x + a.y - b.x); else y = max(y, b.x + b.y - a.x); return getAera(Tri{1, y}); } } int main(){ int n; scanf("%d", &n); s.clear(); while(n--){ Tri a; scanf("%lld%lld", &a.x, &a.y); auto it = s.upper_bound(a); if(it != s.begin()) it--; //第一个x小于等于a.x的位置 if(s.begin() != s.end() && contain(*it, a)){ //a被包含 printf("0 "); continue; } ll ret = getAera(a); for(auto i = it; i != s.end();){ ret -= intersect(a, *i); if(!contain(a, *i) && (*i).x >= a.x) break; auto pre = i++; if(i == s.end()) break; ret += intersect(*i, *pre); } for(auto i = it; i != s.end();){ if(contain(a, *i)) s.erase(i++); else i++; } s.insert(a); printf("%lld ", ret); } return 0; }