因为最近有一门课要求读一篇论文,我在这里记录一下自己学到的东西,希望能更加深刻的理解我学到的东西,内容应该是对原论文中的一些扩展。
前置技能:
关于密钥共享,主要参考了这篇博客 https://blog.csdn.net/shangsongwww/article/details/90266937
(1)加法共享
对于一个数a,拆成a0,a1两部分,分发给服务器S0,S1。对于b也是。那么我们求a+b就可以了,让S1发给S0 a1+b1,然后S0把手里的值都加起来,就可以算出a+b了,而并不知道a和b的数具体是多少。
(2)乘法共享
对于两个数a,b,我们现在要做到的就是给两个服务器a0,b0,a1,b1,使得服务器能在不知道其中具体值的情况下,做到知道a*b的值。
这是我们需要一个三元组,u,v,w.这是预先算好的,w=u*v。u和v都是随机的。按照加法分享的方式分给两个服务器。这时候,我们要做的就是求a*b了。来推一波式子:
假设m=a-u,n=b-v
a*b=(a-u+u)*(b-v+v)=(m+u)*(n+v)=m*n+m*v+u*n+w
我们看这个m和n是一种减法的关系,和上面的加法分享是类似的,所以我们可以m和n求出来,然后求出m*v+u*n也是很加法分享是一种类似的思路,就是带上了一个参数而已。
II. PRELIMINARIES
A. Machine Learning
(a)Linear regression:
我在这里看的是这一篇博客:https://blog.csdn.net/fengxinlinux/article/details/86556584,写的真的很好,看过一遍就能懂论文中写的是什么了。
关于Mini-batch,这里的公式没怎么看懂,我算的矩阵大小应该不是这样啊。
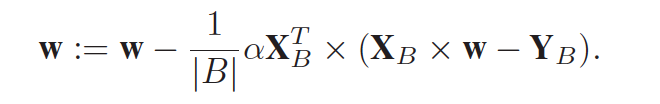
这里XB是n*d的,w应该是d*d的,但是w是d*d的怎么迭代的啊,相当于算出来了n组w值,最后在一起平均一下吗?这里的细节不太明白。
这懂了这个之后直接来看
IV. PRIVACY PRESERVING MACHINE LEARNING
A. Privacy Preserving Linear Regression
训练数据分别被S0,S1所共享,分别持有<X>0,<Y>0和<X>1,<Y>1。然后提了一句这个秘密份额是可以由客户端分配的,或者可以把一部分用S0的公钥加密后,把这个和另外一部分的纯文本发给S1,然后S1再给S0。(虽然我不知道这有啥用,可能是客户端只需要与一个服务器接触吧,减少了客户的计算量?没理解这部分在干啥)。对于这部分,把输入输出的XY数据都分成两份交给两个服务器,任何一个服务器都无法还原客户的数据,但是可以做到一起计算,生成出模型出来,这样就做到了隐私保护。然后在做线性回归的过程中系数矩阵w也是一直被共享成w0和w1的。
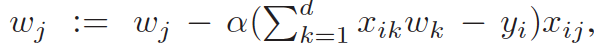
然后对这个公式做一下解释,这个公式是梯度下降的公式,为了进一步优化损失函数在求偏导的路上,找如何更新w,具体可以看上面提到的连接,阿拉法是学习速率。
然后因为这个式子中只有乘法和除法,可以将其中的东西都用之前的分享方法进行隐藏。
后来就是推广到矩阵了,之前的式子是一个个单个的数字进行迭代,其实他们排在一起可以同时算出来,就能推广到矩阵了,这里不难理解。
然后要用到之前的分组方法加速,希望能迭代好多组。