三元环是一个不怎么常见的黑科技,它的求解方法是一种基于分块思想的方法,比较简单好写,在这里介绍一下三元环的计数方法及正确性与时间复杂度证明。
对于一个$n$个点$m$条边的无向图,三元环是指对于图上的三个点,两两点之间都直接有边相连,这三个点组成的环就是三元环。
三元环的计数方法:记录图中每个点的度数,对于每条边将它定向。对于一条边,将度数大的点指向度数小的点,如果度数相同就将编号小的点指向编号大的点。计数时枚举每个点,对于每个点$x$枚举它的出边,并将出边指向的点$y$打标记,对于所有出边指向的点$y$再枚举出边,如果这个出边指向的点$z$被打了标记,那么$x,y,z$就组成了一个三元环。时间复杂度为$O(msqrt{m})$。
对于这个方法只需要证明三点:
1、将边定向后的图是有向无环图($DAG$)
这个很好证明,因为按照上述定向规则,我们称$x$连向$y$表示$x$比$y$大,那么任意两个点的大小关系是固定的,每个点只会向比它小的点连边,所以一定构成了有向无环图。
2、每个三元环只会被统计一次
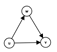
如图所示,因为三元环上的边是定向的,而且每个点只会枚举出边,所以每个三元环被统计的情况是唯一的。
3、时间复杂度为$O(msqrt{m})$
考虑时间复杂度分为两部分:一部分为每个点枚举出边,另一部分为每个出边指向的点枚举出边。
第一部分时间复杂度显然为$O(n+m)$,而第二部分我们分类讨论:
如果一个点的出度大于$sqrt{m}$,指向它的点出度一定要比它大,这样的点最多$sqrt{m}$个,时间复杂度为$O(msqrt{m})$
如果一个点的出度小于$sqrt{m}$,指向他的点最多有$n$个,时间复杂度为$O(nsqrt{m})$
综上所述,时间复杂度为$O(msqrt{m})$
三元环的题只找到了三道: