已经有很多博客已经将sift特征提取算法解释的很清楚了,我只是记录一些我不明白的地方,并且记录几个理解sift特征比较好的博客。
1. http://aishack.in/tutorials/sift-scale-invariant-feature-transform-introduction/
2. http://blog.csdn.net/abcjennifer/article/details/7639681/
3.http://blog.csdn.net/xiaowei_cqu/article/details/8067881
4.https://en.wikipedia.org/wiki/Scale_space
5.http://blog.csdn.net/pi9nc/article/details/23302075
一、说到sift特征就不得不提什么是尺度空间(scale-space)
一个感观的认识就是人眼在看一个物体的时候远和近时,物体在视网膜上成像。尺度空间中各尺度图像的模糊程度逐渐变大,能够模拟人在距离目标由近到远时目标在视网膜上的形成过程。在图像形成的过程中不可避免的会有将摄像头拉近或者拉远的操作,而这种操作带来的就是尺度的变化,这也是想寻找尺度不变特征的原因。
一个理论上的解释参考WIKI:The main type of scale space is the linear (Gaussian) scale space:

就是说尺度空间就是用不同参数t的高斯核去卷积图像得到的。我们可以从参考材料的1和4中可以看到模糊的例子,上面的t是方差,也就是下文将要说的sigma的平方。
二、尺度不变性
参考这个网址:http://dsp.stackexchange.com/questions/397/why-is-the-difference-of-gaussians-scale-space-scale-invariant?rq=1,对尺度不变性给出了一个简单的回答:
The term "scale-invariant" means the following here. Let's say you have image I, and you have detected a feature (aka an interest point) f at some location (x,y) and at some scale level s. Now let's say you have an image I', which is a scaled version of I (downsampled, for instance). Then, if your feature detector is scale-invariant, you should be able to detect the corresponding feature f' in I' at the corresponding location (x',y') and corresponding scale s', where (x, y, s) and (x', y', s')are related by the appropriate scaling transformation.
我的理解就是说如果你的图片I在尺度s下被检测出在(x,y)下具有特征点f,那么如果你有另一张在其他尺度s'下的图片I',如果你的特征检测器是尺度不变的话,你应该可以检测出对应的特征点f',位置于(x',y')使得(x,y,s)与(x',y',s')只差一个放缩变换。下面有一个我自己的理解,不一定正确,有时间我在看看尺度理论。假设在sigma尺度下找到的特征点为(x,y,sigma)则有下面这个等式成立,这里的sigma是方差:

如果另一张图片在另外一个尺度下,也就是将图片I进行模糊后,在求极值寻找特征点会有以下的式子(误,只是一种数学上的感觉):
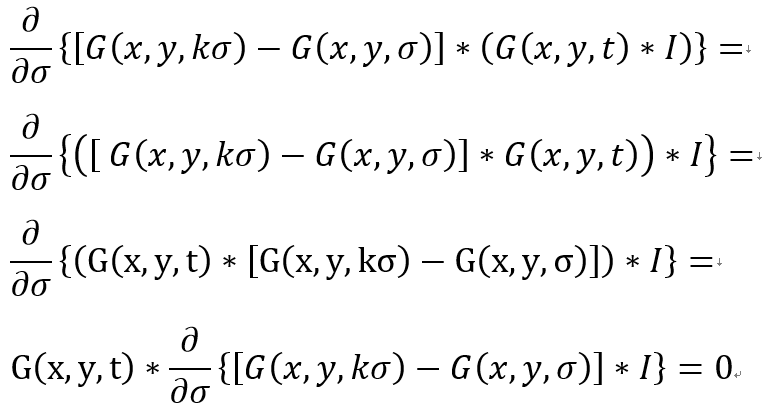
(这里的t和一中的t不是同一个)我们用G(x,y,t)对图片I进行模糊得到另外一个尺度的图片,然后我们再用DOG对其进行卷积并在尺度sigma下求极值。根据卷积的结合律(可以参考WIKI:https://en.wikipedia.org/wiki/Convolution)就有上式第二行的结果,然后根据卷积的交换律有第三行的结果,然后t和sigma是独立的或者说t是常量所以从求导符号中提出来,然后根据上上式就会发现上上式求得的极值点也是另一个尺度图片下求得的极值点。用一篇论文的一个图片例子:
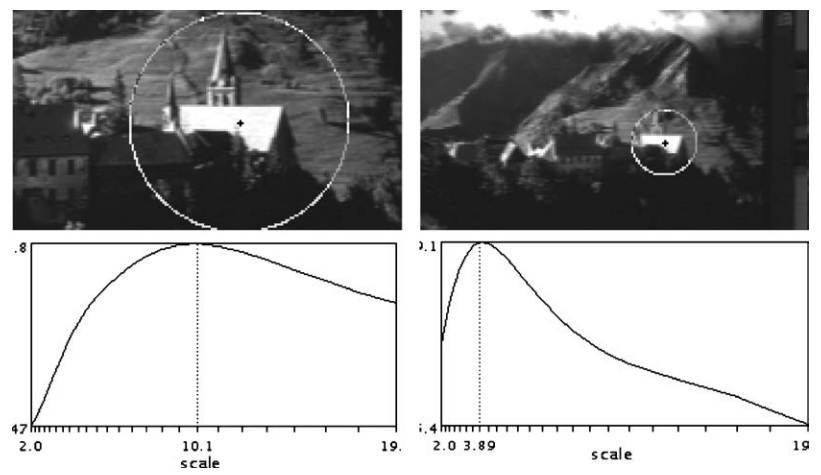
上图就发现在相对应的特征点是不同scale上的极值点。
三、为什么要用GOG(difference of Gaussian)去替换LOG(Laplancian of Gaussian)
根据这篇文章:http://www.scholarpedia.org/article/Scale_Invariant_Feature_Transform

也就是说Lindeberg在他的两篇关于blob detection论文中发现blob可以通过scale-normalized Laplacian检测出来,那么什么是尺度归一化的拉普拉斯呢?文章又给出了定义,就是上图的第一个公式(s是方差,也就是sigma的平方)。然后在sift中为什么不用尺度归一化的拉普拉斯变换来计算尺度不变的特征点呢?原因是他又发现DOG是LOG的一个近似,而且据说计算速度更快。是怎么证明DOG是LOG的近似呢?这里我来证明一下。这里有几个定义混淆了,我们先区分一下:
1. 拉普拉斯变换,对函数f(x,y)进行拉普拉斯变换就是求二阶偏导数相加:
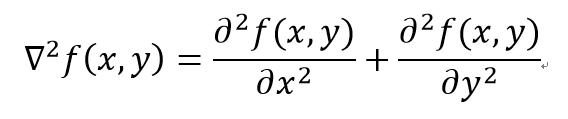
2. Laplacian of Gaussian (LOG)
![]()
3. 尺度不变的拉普拉斯变换,根据上面文章第一个公式,由于卷积与导数的运算法则,可以知道尺度不变的拉普拉斯变换是:
![]()
4. Difference of Gaussian (DOG)
![]()
5. 二维的高斯分布,均值为0,方差为sigma平方
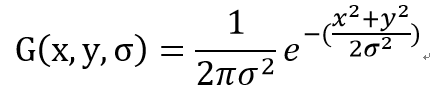
6. 证明DOG是LOG的一个近似,首先我们证明下面这个式子成立:
![]()
非常简单,只要你知道如何求高斯函数的导数就好了,等式右边的求导过程可以参考网址:http://fourier.eng.hmc.edu/e161/lectures/gradient/node8.html, 在这里我给一个简单的证明。

因此等式右边等于:
![]()
等式左边对sigma进行求导,求导过程非常简单,我就不打算记录很详细了:
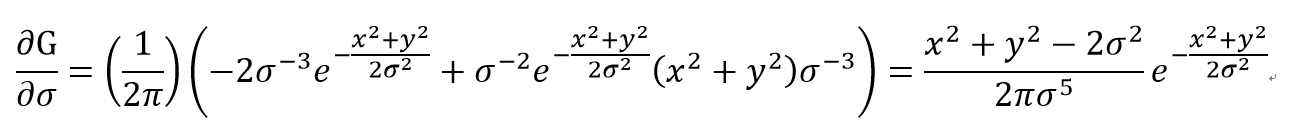
因此我们左边等于右边,只需稍微化简一下。因此有下面这个成立:
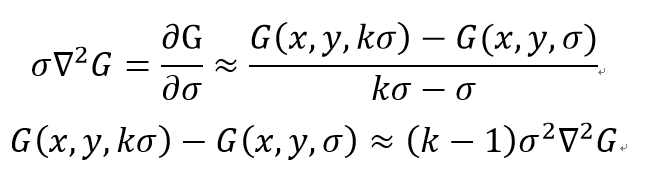
因此DOG和尺度归一化的LOG只差一个常数因子(k-1)并不影响极值点位置的求取,见博客(blog.csdn.net/pi9nc/article/details/23302075)。整个近似就证明完毕(*)。
上面只是说了一些我对尺度空间明白的地方,当然还有很多不明白的地方等我以后看懂了再回头记下,又回到sift特征,还有几个主题想记录一下。
四、我们在每座高斯金字塔中额外的新增了3层,为什么能够满足尺度变化的连续性。我觉得参考文章2中已经解释的很清楚,我直接转和复制一下,并且附上我自己手绘的一幅图便于理解:


暂时明白了这么多,以后再加,剩下的理解在源码中注释了,见另外的一篇博客