一、堆排序算法的基本特性
时间复杂度:O(n*lgn)
最坏:O(n*lgn)
空间复杂度:O(1)
不稳定。
堆排序是一种选择排序算法,与关键字的初始排列次序无关,即就是在最好,最坏,一般的情况下排序时间复杂度不变。对包含n个数的输入数组,平均时间为O(nlgn),最坏情况(已经排好序)也是是O(nlgn),最好情况(完全无序)也是O(nlgn)。由于不但时间复杂度少,而且空间复杂度也是最少的,所以是用于排序的最佳选择。因为,基于比较的排序,最快也只能达到O(nlgn),虽然快排也可以达到这个这个水平,但是快排的时间复杂度是跟关键字的初始排序有关,最坏的情况退化成O(n^2),而且快排的空间复杂度是O(n*lgn)。
二、堆的定义
n个元素的序列{k1,k2,…,kn}当且仅当满足下列关系之一时,称之为堆。
情形1:ki <= k2i 且ki <= k2i+1 (最小化堆或小顶堆:左、右子孩子的值比父结点的值都大)
情形2:ki >= k2i 且ki >= k2i+1 (最大化堆或大顶堆:左、右子孩子的值比父结点的值都小)
其中i=1,2,…,n/2向下取整;
若将和此序列对应的一维数组(即以一维数组作此序列的存储结构)看成是一个完全二叉树,则堆的含义表明,完全二叉树中所有非叶子结点的值均不大于(或不小于)其左、右孩子结点的值。
由此,若序列{k1,k2,…,kn}是堆,则堆顶元素(或完全二叉树的根)必为序列中n个元素的最小值(或最大值)。
例如,下列两个序列为堆,对应的完全二叉树如图:

若在输出堆顶的最小值之后,使得剩余n-1个元素的序列重又建成一个堆,则得到n个元素的次小值。如此反复执行,便能得到一个有序序列,这个过程称之为堆排序。
堆排序(Heap Sort)只需要一个记录元素大小的辅助空间(供交换用),每个待排序的记录仅占有一个存储空间。
三、堆的存储
一般用数组来表示堆,若根结点存在序号0处, i结点的父结点下标就为(i-1)/2。i结点的左右子结点下标分别为2*i+1和2*i+2。
(注:如果根结点是从1开始,则左右孩子结点分别是2i和2i+1。)
如第0个结点左右子结点下标分别为1和2。
如大顶堆如下:
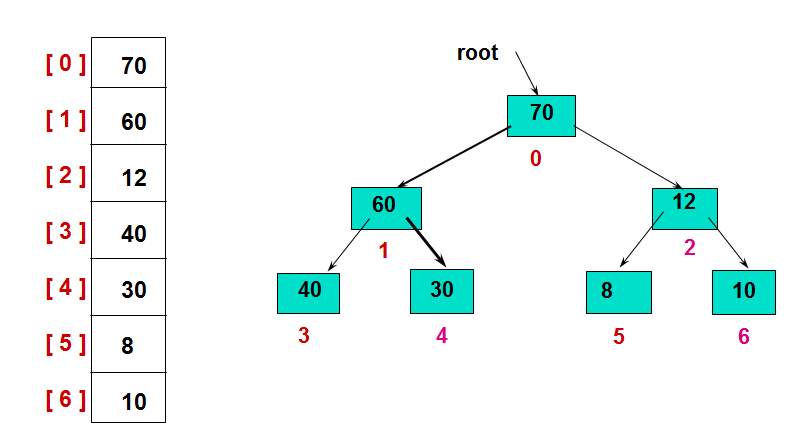
左图为其存储结构,右图为其逻辑结构。
四、堆排序的实现
实现堆排序需要解决两个问题:
1.如何由一个无序序列建成一个堆?
2.如何在输出堆顶元素之后,调整剩余元素成为一个新的堆?
先考虑第二个问题,一般在输出堆顶元素之后,视为将这个元素排除,然后用表中最后一个元素填补它的位置,自上向下进行调整:首先将堆顶元素和它的左右子树的根结点进行比较,把最小的元素交换到堆顶;然后顺着被破坏的路径一路调整下去,直至叶子结点,就得到新的堆。
我们称这个自堆顶至叶子的调整过程为“筛选”。
从无序序列建立堆的过程就是一个反复“筛选”的过程。
构造初始堆
初始化堆的时候是对所有的非叶子结点进行筛选。
假设有n个元素的堆,那么最后一个非叶子元素的下标是[n/2]-1(向下取整),所以筛选只需要从第[n/2]-1个元素开始,从后往前进行调整。
比如,给定一个数组,首先根据该数组元素构造一个完全二叉树。
然后从最后一个非叶子结点开始,每次都是从父结点、左孩子、右孩子中进行比较交换,交换可能会引起孩子结点不满足堆的性质,所以每次交换之后需要重新对被交换的孩子结点进行调整。
进行堆排序
有了初始堆之后就可以进行排序了。
堆排序是一种选择排序。建立的初始堆为初始的无序区。
排序开始,首先输出堆顶元素(因为它是最值),将堆顶元素和最后一个元素交换,这样,第n-1个位置(即最后一个位置)作为有序区,前n-2个位置仍是无序区,对无序区进行调整,得到堆之后,再交换堆顶和最后一个元素,这样有序区长度变为2。。。
不断进行此操作,将剩下的元素重新调整为堆,然后输出堆顶元素到有序区。每次交换都导致无序区-1,有序区+1。不断重复此过程直到有序区长度增长为n-1,排序完成。
堆排序实例
首先,建立初始的堆结构如图:
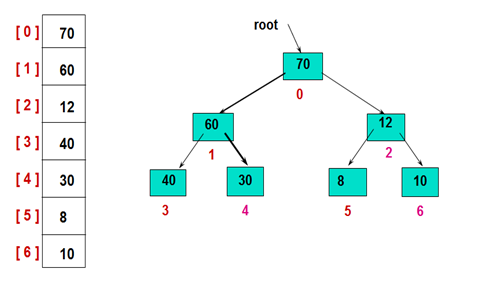
然后,交换堆顶的元素和最后一个元素,此时最后一个位置作为有序区(有序区显示为黄色),然后进行其他无序区的堆调整,重新得到大顶堆后,交换堆顶和倒数第二个元素的位置……
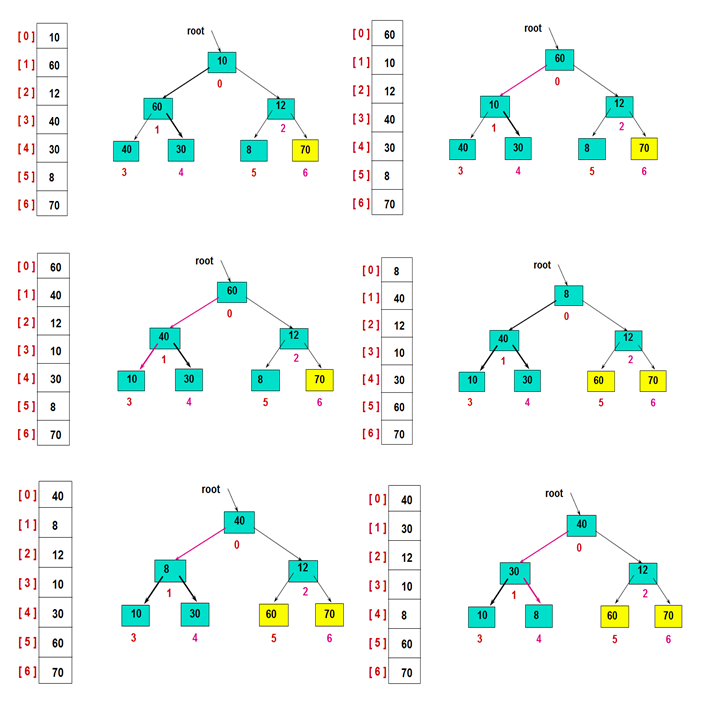
重复此过程:
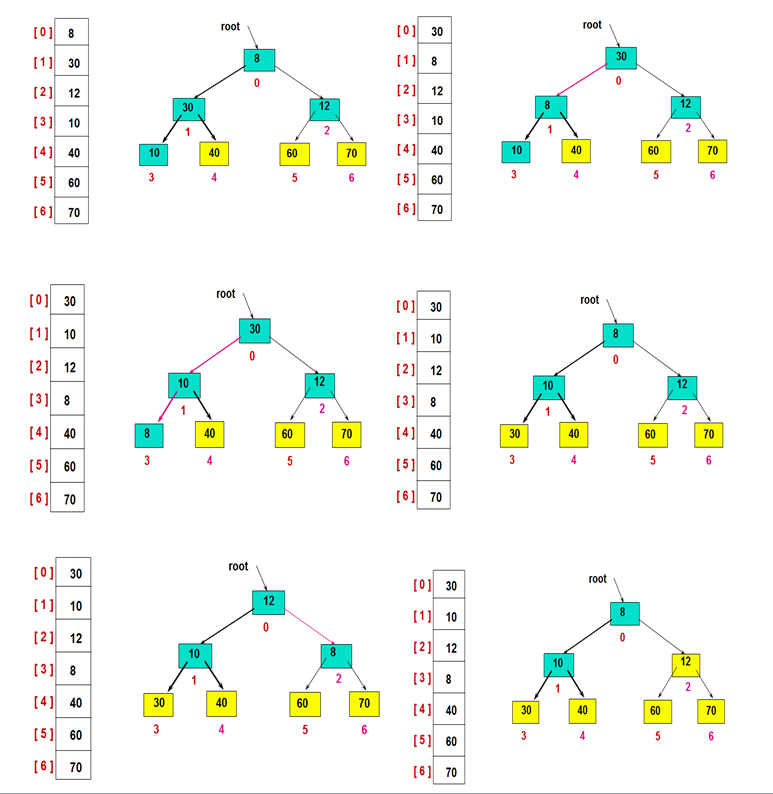
最后,有序区拓展完成,即排序完成:

由排序过程可见,若想得到升序,则建立大顶堆,若想得到降序,则建立小顶堆。
五、代码
假设排列的元素为整型,且元素的关键字为其本身。
因为要进行升序排列,所以用大顶堆。
根结点从0开始,所以i结点的左右孩子结点的下标为2i+1和2i+2。
import java.util.Scanner; /** * 堆排序 * 时间复杂度:O(n*lgn) * 空间复杂度:O(1) * @author breeze * */ public class HeapSort { /** * 堆排序的主方法 * * @param array * @return */ public static int[] sortHeap(int[] array) { buildHeap(array);// 构建堆 int n = array.length;//数组中元素的个数 for (int i = n - 1; i >= 1; i--) { swap(array, 0, i);//交换首尾元素 adjustHeap(array, 0, i);//调整堆 } return array; } /** * 构建大顶堆堆 * 从最后一个非叶子结点开始调整堆。每次都是从父结点,左节点,右结点三者中选最大值与父结点交换 * @param array */ private static void buildHeap(int[] array) { int n = array.length;// 数组中元素的个数 for (int i = n / 2 - 1; i >= 0; i--)//i= n/2-1 表示最后一个非叶子结点的索引值 adjustHeap(array, i, n); } /** * 调整堆 * @param A * @param idx * @param max 堆的大小 */ private static void adjustHeap(int[] A, int idx, int max) { int left = 2 * idx + 1;// 左孩子的下标(如果存在的话) int right = left + 1;// 左孩子的下标(如果存在的话) int largest = 0;// 寻找3个节点中最大值节点的下标 if (left < max && A[left] > A[idx])//左孩子的值比父结点的值大 largest = left; else largest = idx; if (right < max && A[right] > A[largest]) largest = right; if (largest != idx) { swap(A, largest, idx);//从左节点,右结点中选最大值与父结点交换 adjustHeap(A, largest, max); } } private static void swap(int[] array, int i, int i2) { int temp = array[i]; array[i] = array[i2]; array[i2] = temp; } public static void main(String[] args) { Scanner sc = new Scanner(System.in); while(sc.hasNextLine()){ String str = sc.nextLine(); //获取一行 String[] words = str.trim().split(" ");//把一行的数据,分割为单个的数据的数组 int length = words.length; //字符串还需要转为int,或者其他的类型 int[] params = new int[length]; for (int i = 0;i<length;i++){ if ("".equals(words[i]) || " ".equals(words[i])) continue; params[i] = Integer.parseInt(words[i]); } //调用需要测试的函数 int[] array = sortHeap(params); //打印结果 for(int i : array){ System.out.print(i+" "); } } } }
图片和内容参考:http://www.cnblogs.com/mengdd/archive/2012/11/30/2796845.html