1. Definiation
A Tree is a collection of nodes. The collection can be empty; otherwise, a tree consists of a distinguished node r, called root and zero or more nonempty (sub) trees T1, T2, T3, ..., Tn, each of whose roots are connected by a directed edge from r.
no chidlren are known as leaves
Nodes with same parent are siblings
Path: a path from node n1 to nk is defined as a sequence of nodes n1, n2, ... ,nk, such that ni is the parent of ni+1 for 1<=i<k.
Length: the length of the path is the number of edges on the path.
Depth: the length of the unique path from the root to ni
Height:the length of the longest path from ni to a leaf
If there is a path from n1 to n2, then n1 is an ancestor of n2 and n2 is a descentdant of n1. If n1!=n2, then n1 is a proper ancestor of n2...
有序树: 子树次序不能互换;
森林: 互不相交的树的集合
2、树的储存结构
(1)双亲表示法
用连续储存结构来储存树,每个节点不仅储存他们各自的数据,而且储存他们双亲的下标
const int max_size=100;
template<typename Object>
struct node
{
Object data;
int index; //the index of its parent
};
template<typename Object>
struct tree
{
node nodes[max_size];
int r; //the position of root
int n; //the number of nodes
};
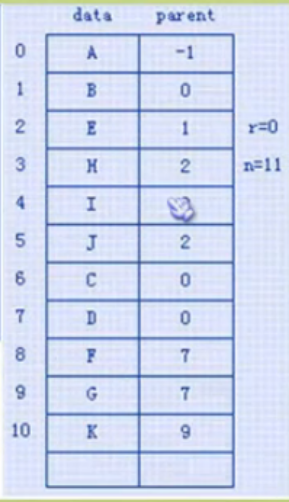

找双亲的时间复杂度o(1)
当我需要找儿子时需要遍历整棵树去寻找
对该结构作出改进,将数组中数据扩充即可
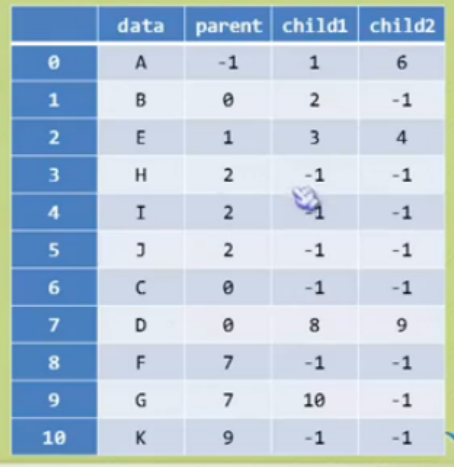
当我们要找兄弟呢?

扩充数组解决问题
(2)孩子表示法
树的每个节点有多个子节点,考虑用多重链表解决
方案一:根据树的度数,声明足够空间存放子树指针节点。

浪费空间
方案二:每个节点储存自己的度数,节省空间

但实现起来麻烦
方案三:双亲孩子表示法

既有指针指向自己的孩子,也有index指向自己双亲
const int max=100;
typedef struct Cnode
{
int child; //孩子节点的下标
struct Cnode* next; //指向下一个孩子节点的指针
} *Childptr;
//表头结构
template<typename Object>
typedef struct
{
Object data;
int parent;
Childptr firstChild;
} CTBox;
//树结构
typedef struct
{
CTBox nodes[max];
int r,n;
};
(3)孩子兄弟表示法
孩子兄弟表示法是一种链式储存结构,每个节点储存了孩子与兄弟的信息
template<typename Object>
struct node
{
Object data;
node* firstchild;
node* nextsibiling;
};