
Sample Input
5 2 4 2 3 1
Sample Output
3

TJ:
将输入数据画成一个有向图,于是答案就是这个图的最小强连通分量(一个点不算)的大小。
这个应该不难理解吧~~~
上图!!!!
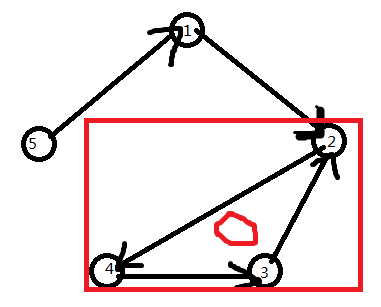
所以,这题就变成了一个类似“Tarjan”的东东。
温馨提示:每个点只有一条出边,所以不要像我一开始一样傻傻地打一个“前向星”。
~~~~~~~~~~~上代码!
#include<bits/stdc++.h>
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define min(a,b) (a<b?a:b)
using namespace std;
int n,m,x,y,ans,S,tot;
bool bz[200010],bz1[200010];
int a[200010],t[200010];
void dg(int x){
if(bz1[t[x]]){
if(bz[t[x]])ans=min(a[x]-a[t[x]]+1,ans);
bz[x]=0;
return;
}
bz[t[x]]=bz1[t[x]]=1;
a[t[x]]=a[x]+1;
dg(t[x]);
bz[x]=0;
}
int main(){
freopen("message.in","r",stdin);
freopen("message.out","w",stdout);
scanf("%d",&n);
fo(i,1,n){
scanf("%d",&t[i]);
}
ans=2147483647;
fo(i,1,n){
if(bz1[i])continue;
bz1[i]=1;
bz[i]=1;
a[i]=1;
dg(i);
}
printf("%d
",ans);
return 0;
}
我的Tarjan是手推的,感觉上差不多,与正常Tarjan的细微差距请无视