695. 岛屿的最大面积

题目
解题思路
代码
优化
代码
优秀提交学习

toc

题目

给定一个包含了一些 0 和 1 的非空二维数组 grid 。

一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0 。)

示例 1:

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。

示例 2:

[[0,0,0,0,0,0,0,0]]
对于上面这个给定的矩阵, 返回 0。

注意: 给定的矩阵grid 的长度和宽度都不超过 50。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/max-area-of-island
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路

本题需要找出聚集1的最大个数(上下左右相连)。可一条路走到黑式检测、选择上下左右任一个方向，检测是否是1，是1继续检测同方向，不是1则换方向继续一条路走到黑，直到检测不到1，此时统计完聚集1的个数。即深度优先搜索遍历

代码

class Solution {
public:
    int DFS(const std::vector<std::vector<int>>& grid, int iXSize, int iYSize, 
            int x, int y, std::vector<std::vector<int>>& vecvecVisited){
        //边界检查
        if(x < 0 || x >= iXSize || y < 0 || y >= iYSize)
            return 0;        
        //当前坐标不是岛屿或已访问
        if(0 == grid[y][x] || 1 == vecvecVisited[y][x])
            return 0;
        //当前位置已访问标记
        vecvecVisited[y][x] = 1;
        //返回当前坐标的面积大小 及 上、下、左、右 位置面积
        return 1 + DFS(grid, iXSize, iYSize, x, y + 1, vecvecVisited) + DFS(grid, iXSize, iYSize, x, y - 1, vecvecVisited)
             + DFS(grid, iXSize, iYSize, x - 1, y, vecvecVisited) + DFS(grid, iXSize, iYSize, x + 1, y, vecvecVisited);
    }


    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int iMaxArea = 0;
        int iYSize = grid.size(), iXSize = grid.front().size();
        std::vector<std::vector<int>> vecvecVisited(50);
        for(auto & elem : vecvecVisited){
            elem.resize(50);
        }

        for(int y = 0; y < iYSize; y++){
            for(int x = 0; x < iXSize; x++){
                iMaxArea = std::max(iMaxArea, DFS(grid, iXSize, iYSize, x, y, vecvecVisited));
            }
        }
        return iMaxArea;
    }
};

执行消耗内存分布图表更是惨不忍睹的仅超过6%，太惨就不贴图了...

优化

1. visited是二维的，二维的vector不同于二维的数组：

• vector对象本身与其实际存储元素的空间是分开的，管理存储空间的vector对象本身也会占用内存空间。可降低vector对象个数来减少空间占用
• 二维数组本质是一维数组语法糖，实际还是连续空间；但二维vector中，内层与外层vector的存储空间是真实独立的，这就意味着每次访问均会多一次寻址操作，对使用缓存也不友好。可将二维vector降维提高性能

1. grid的大小是固定的，可将每次调用传入dfs函数的size，提为类成员，可减少传参个数、减少调用时拷贝的字节数，可以减少内存消耗(但测试后发现内存消耗并未减少，消耗的运行时间反倒增多，时间增多可以理解，因为需寻址this指针访问size成员，肯定没直接访问栈上的size快。但是内存消耗没减少就有点想不通了)

代码

class Solution {
private:
    int m_iYSize = 0;
    int m_iXSize = 0;
public:
    int DFS(const std::vector<std::vector<int>>& grid, int x, int y, std::vector<int>& visited){
        //边界检查
        if(x < 0 || x >= m_iXSize || y < 0 || y >= m_iYSize)
            return 0;        
        //当前坐标不是岛屿或已访问
        if(0 == grid[y][x] || 1 == visited[y * m_iXSize + x])
            return 0;
        //当前位置已访问标记
        visited[y * m_iXSize + x] = 1;
        //返回当前坐标的面积大小 及 上、下、左、右 位置面积
        return 1 + DFS(grid, x, y + 1, visited) + DFS(grid, x, y - 1, visited)
             + DFS(grid, x - 1, y, visited) + DFS(grid, x + 1, y, visited);
    }


    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int iMaxArea = 0;
        m_iYSize = grid.size(), m_iXSize = grid.front().size();
        std::vector<int> visited(2500, 0);

        for(int y = 0; y < m_iYSize; y++){
            for(int x = 0; x < m_iXSize; x++){
                if(0 == grid[y][x])    //仅在grid中0多时有用
                    continue;

                iMaxArea = std::max(iMaxArea, DFS(grid, x, y, visited));
            }
        }
        return iMaxArea;
    }
};

终于接近平均水平了，不过内存消耗依旧很惨。仅7%...

优秀提交学习

下图代码来自LeetCode中超越100%的提交代码

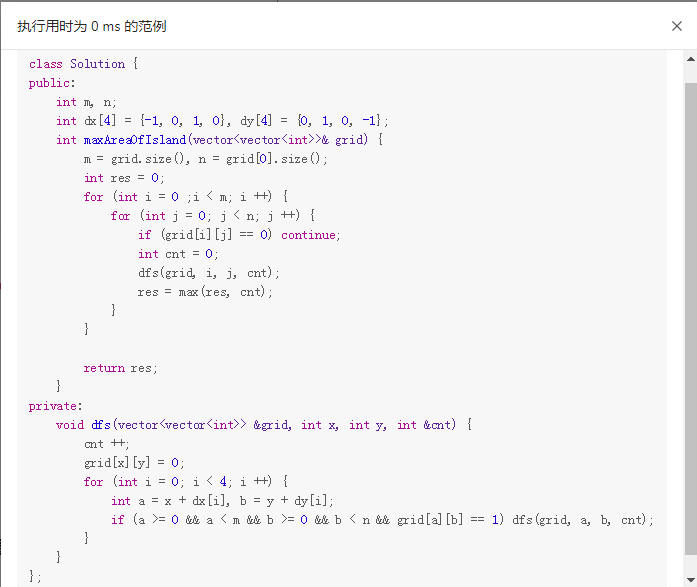
不得不说，超越100%的代码真是挺新奇的，常规思路都是在函数入口判断边界，判断返回条件，导致了很多重复问的判断，图中的代码直接将判断交给了上层，由上层判断来避免额外的性能开销。
哈哈，我也知道为什么我的内存消耗

来自为知笔记(Wiz)