redis源码学习之zskiplist

参考《Redis 设计与实现》 (基于redis3.0.0) 作者:黄健宏
学习redis3.2.13

介绍
跳表的结构
节点zskiplistNode
管理结构定义
跳表的创建与释放
插入节点
计算节点最大层数
删除节点
移除待删节点
释放节点
性能比较
参考资料

toc

介绍

zskiplist是一个跳表，或者说跳跃表。它是一个有序链表，通过额外的空间与类似二分的查找算法，使得其对数据的查找、插入、删除操作得以快速完成，这些操作的平均时间复杂度为O(logN)，最坏情况为O(N)

链表的示意图如下：

跳表的性质：

• 跳表的每个节点可以拥有不同的层级，节点的层数由抛硬币的形式确定，跳表是概率性数据结构
• 跳表的每一层都可以看做一个有序链表，只是层级越高，链接的节点就越少，查找时跳过的节点也就越多
• 跳表的最底层连接了全部的节点，如果一个节点在K被链接，那么在K层以下，该节点同样会被链接
  查找示意图：
  
  从图中，可以看到，高层链表节点稀疏，跳过的节点多，越往下节点越多，最底层链表拥有全部节点，通过从高层链表往下搜索，可以跳过很多节点，提高查找性能
  注：示意图中多了尾部的哨兵节点，zskiplist不含此节点

跳表的结构

节点zskiplistNode

typedef struct zskiplistNode {
    //指向具体对象， 这里暂时抛开robj的类型，只关注节点结构
    robj *obj;            
    //节点的分值，节点排序的依据，分值小的在前，数值递增排序
    double score;
    //后退指针，用于连接前驱节点，反向遍历时使用
    struct zskiplistNode *backward;
    //层级数组
    struct zskiplistLevel {
        //前进指针，用于连接后继节点
        struct zskiplistNode *forward;
        //指针前进跨度，记录当前节点到后继节点的距离
        //当前节点为尾节点时，值为0，表示不与任何节点连接
        unsigned int span;
    } level[];
} zskiplistNode;

节点内的层级又是一个柔性数组，使用柔性数组的好处前面已经多次说明，这里就不再赘述了，由于从上层往下层查找，并且被上层链接的节点一定会被下层链接，所以也不用记录柔性数组长度也不会发生内存访问错误。
使用柔性数组作为层级来在每层共用节点，而不是将每层当作单独的链表，使用指向下层的指针连接， 减少了实现的复杂度，节省了内存，可以说真的很巧妙

管理结构定义

typedef struct zskiplist {
    //头、尾节点，头结点不存储数据
    struct zskiplistNode *header, *tail;
    //跳表拥有节点个数(不计头结点)
    unsigned long length;
    //跳表中层数最高节点的层数(不计头结点)
    int level;
} zskiplist;

跳表的创建与释放

跳表中节点最高层限制在了32，为了从上到下遍历，创建时，将头结点创建为32层，并初始化每一层

#define ZSKIPLIST_MAXLEVEL 32 /* Should be enough for 2^32 elements */

zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;

    zsl = zmalloc(sizeof(*zsl));
    zsl->level = 1;
    zsl->length = 0;
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;
    zsl->tail = NULL;
    return zsl;
}

void zslFree(zskiplist *zsl) {
    zskiplistNode *node = zsl->header->level[0].forward, *next;

    zfree(zsl->header);
    while(node) {
        next = node->level[0].forward;
        zslFreeNode(node);
        node = next;
    }
    zfree(zsl);
}

zskiplistNode *zslCreateNode(int level, double score, robj *obj) {
    zskiplistNode *zn = zmalloc(sizeof(*zn)+level*sizeof(struct zskiplistLevel));
    zn->score = score;
    zn->obj = obj;
    return zn;
}

void zslFreeNode(zskiplistNode *node) {
    decrRefCount(node->obj);
    zfree(node);
}

插入节点

结合示意图来看，更便于理解

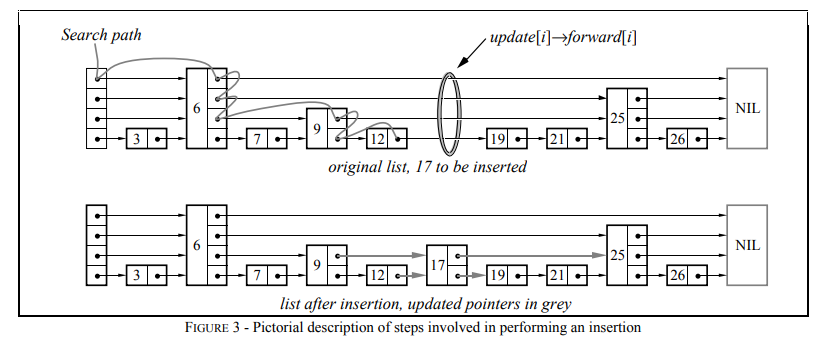
注释已经写得很详细了，就不对代码逻辑进行额外说明了。

zskiplistNode *zslInsert(zskiplist *zsl, double score, robj *obj) {
    //update数组用于记录每层待插入节点的前驱节点
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    //记录每层内，待插节点前驱节点的排名
    unsigned int rank[ZSKIPLIST_MAXLEVEL];
    int i, level;
    //nan无法排序，此处做一个判断
    serverAssert(!isnan(score));
    //由头结点开始往后寻找
    x = zsl->header;
    //由高层向低层，在每层寻找新节点的前驱节点x，完成插入后，前驱节点的后继就是新插入节点
    /*因为节点层数高的概率小，所以层数高的节点少，高层级节点间跨度大，从上层开始找时，可跳过部分节点，所以看似O(n^2)的实现，实际O(NlogN)*/
    for (i = zsl->level-1; i >= 0; i--) {
        /* store rank that is crossed to reach the insert position */
        //当位于顶层节点时，运行到此处，x还指向头结点，未跨过任何节点，跨度为0
        //当不位于顶层节点时，说明当上一层寻找完毕，x刚由上一层切换到本层，由于是同一个节点，所以排名是一样的，记录下来，后续在本层进行寻找时使用
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        //在i层中寻找前驱节点  寻找时，对比分值，分值一致就对比存储对象的大小
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||      
                (x->level[i].forward->score == score &&
                compareStringObjects(x->level[i].forward->obj,obj) < 0))) { //二进制安全对比
            //记录在i层里寻找前驱节点时，经过的跨度
            rank[i] += x->level[i].span;
            //往后继节点迭代
            x = x->level[i].forward;
        }
        //将i层里找到的前驱节点记录，等待后续插入使用
        update[i] = x;
        //i层查找结束，继续从x节点的下一层开始往后寻找
    }
    /* we assume the key is not already inside, since we allow duplicated
     * scores, and the re-insertion of score and redis object should never
     * happen since the caller of zslInsert() should test in the hash table
     * if the element is already inside or not. */
    level = zslRandomLevel();   //计算随机值，后续作为新节点的层数
    //新节点的层数超出了skiplist原有节点中最大已有层数，头结点超出部分的层数将会被使用，将其记录到update供后续使用
    if (level > zsl->level) {
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            update[i] = zsl->header;
            update[i]->level[i].span = zsl->length; 
        }
        zsl->level = level;
    }
    x = zslCreateNode(level,score,obj);
    //由低层往高层插入节点   将新节点x插入于前驱节点update[i]与update[i]后继节点之间，插入通过更新同层内前进指针(后继指针)实现
    for (i = 0; i < level; i++) {
        //先在新节点x的i层后，链接update[i]的后继节点，以避免i层后继节点丢失
        x->level[i].forward = update[i]->level[i].forward;
        //再在update[i]的i层后链接新节点x
        update[i]->level[i].forward = x;

        /* update span covered by update[i] as x is inserted here */
        //rank[0]为新节点x前驱节点在最低层的排名 rank[i]为新节点前驱节点在i层的排名
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
        update[i]->level[i].span = (rank[0] - rank[i]) + 1; //由于新节点插入，前驱节点需增加1
    }

    /* increment span for untouched levels */
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }
    //设置新节点x的后退指针
    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;  //x的后继节点的后退指针
    else
        zsl->tail = x;  
    zsl->length++;  
    return x;
}

计算节点最大层数

在为节点计算层数时，每次循环有0.25的概率将层数增加1
选择0.25而不是0.5是因为前者能提供更好的常数因子

#define ZSKIPLIST_P 0.25      /* Skiplist P = 1/4 */
int zslRandomLevel(void) {
    int level = 1;
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

删除节点

删除节点时，对节点x每层的前驱节点的查找过程与插入节点一致，由于可能有多个节点有同样的score，需要再对比一下object对象是否一致才能进行节点删除操作，删除时先将节点从跳表中移除，再释放节点占用的内存

int zslDelete(zskiplist *zsl, double score, robj *obj) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                compareStringObjects(x->level[i].forward->obj,obj) < 0)))
            x = x->level[i].forward;
        update[i] = x;
    }
    /* We may have multiple elements with the same score, what we need
     * is to find the element with both the right score and object. */
    x = x->level[0].forward;
    if (x && score == x->score && equalStringObjects(x->obj,obj)) {
        zslDeleteNode(zsl, x, update);    //将节点x从跳表中移出
        zslFreeNode(x);    //释放x
        return 1;
    }
    return 0; /* not found */
}
##将节点从跳表中移除

移除待删节点

通过前面的删除函数，我们得到了待删节点x， x在每层的前驱节点数组update
移除时，更新前驱节点在每层的跨度、前进指针，如果x不是尾节点，更新其后置节点的后退指针，否则重设尾节点，最后更新最大层数(当最高层没有连接到任何节点时)及节点个数

void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
    int i;
    for (i = 0; i < zsl->level; i++) {
        if (update[i]->level[i].forward == x) {
            update[i]->level[i].span += x->level[i].span - 1;
            update[i]->level[i].forward = x->level[i].forward;
        } else {
            update[i]->level[i].span -= 1;
        }
    }
    if (x->level[0].forward) {
        x->level[0].forward->backward = x->backward;
    } else {
        zsl->tail = x->backward;
    }
    while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
        zsl->level--;
    zsl->length--;
}

释放节点

释放时，减少被存储对象的引用计数，并释放节点本身占用的内存

void zslFreeNode(zskiplistNode *node) {
    decrRefCount(node->obj);
    zfree(node);
}

性能比较

参考资料

Skip Lists: A Probabilistic Alternative toBalanced Trees
Skip Lists

来自为知笔记(Wiz)