又是八皇后问题。
似乎每种语言中都会出现八皇后问题来告诉你递归算法怎么玩。
让我们先百度一下八皇后问题。于是你发现了百度百科,好长的词条,里面基本包括了所有主流语言的例程。让我们点击Python看一下。
我了个大槽,这是什么玩意,木有缩进,而且那个库也没见过,趁机搜一下。
好像是迭代器里面的东西。迭代器又是什么。 好吧,一个算法问题已经引出了另一个常识问题了。让我们先停在这里吧。去参考另一篇日志吧,还没写。><
我修复了下上面的程序。
from itertools import permutations for vec in permutations(range(8)): if (8 == len(set(vec[i]+i for i in range(8)))== len(set(vec[i]-i for i in range(8)))): print vec
显然是可以运行的。牛逼吧。
但是我们可以知道,这里面是有重复的,因为从棋盘是对称的,每行判别的方法不可避免的出现重复解。但这是正确的完整解92个。
这个程序对于我们初学者来说太过强大了,不过它完美的体现了Python的优美。
让我们看一看比较普通的想法。
好像直到现在我们还不知道什么是八皇后问题,看一下哈。
在8X8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
就是类似于这种布局。
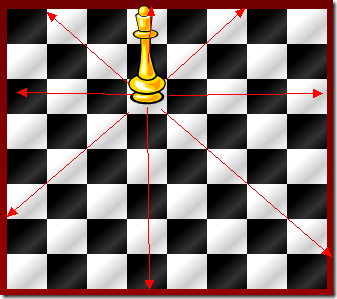
如果我们在棋盘的的任何一个位置放一个皇后,
那么我们就可以得到
这八个方向不能有另外的皇后了,根据这个现象,我们可以肯定,一行有且只有一个皇后,每一列有且只有一个皇后。
我们先预想一个循环,对每一排的每个位置编号0~7 。
我们对每一个位置都应该有可行性判定,即该位置的上下左右,正负对角线有没有皇后,如果有就跳过该位置。
这样的做法应该有几个数组来保存行列,正负对角线状态,让我们先定义全局变量,并且做一些初始化工作。
global col #定义一些全局变量 global row global pos_diag global nag_diag global count ''' =========================================================== ''' col = [] #矩阵列的列表,存储皇后所在列,若该列没有皇后,则相应置为1,反之则0 row = [] #矩阵行的列表,存放每行皇后所在的列位置,随着程序的执行,在不断的变化中,之间输出结果 pos_diag = [] #正对角线,i-j恒定,-7~0~7,并且b(i)+7统一到0~14 nag_diag = [] #负对角线,i+j恒定,0~14 count = 0 for index in range(0, 8): #一些初始化工作 col.append(1) row.append(0) for index in range(0, 15): pos_diag.append(1) nag_diag.append(1)
这样,我们有了一张宏观的表,告诉我们哪一行,哪一列,那几排对角线上面有皇后。
然后让我们定义判定程序。
def do_queen(i): ''' 生成所有正确解 @param i: 皇后的数目,即第几个皇后。从0计数 ''' for j in range(0, 8): #依次尝试0~7位置 if col[j] == 1 and pos_diag[i-j+7] == 1 and nag_diag[i+j] == 1: #若该行,正对角线,负对角线上都没有皇后,则放入i皇后 row[i] = j col[j] = 0 #调整各个列表状态 pos_diag[i-j+7] = 0 nag_diag[i+j] = 0 if i < 7: do_queen(i+1) #可递增或递减 else: print row #产生一个结果,输出 col[j] = 1 #恢复各个列表状态为之前的 pos_diag[i-j+7] = 1 nag_diag[i+j] = 1
把这两段程序拼接起来就完成了,下面给出完整的算法。
global col #定义一些全局变量 global row global pos_diag global nag_diag global count def output(): ''' 输出一种有效结果 ''' global count print row count += 1 def do_queen(i): ''' 生成所有正确解 @param i: 皇后的数目 ''' for j in range(0, 8): #依次尝试0~7位置 if col[j] == 1 and pos_diag[i-j+7] == 1 and nag_diag[i+j] == 1: #若该行,正对角线,负对角线上都没有皇后,则放入i皇后 row[i] = j col[j] = 0 #调整各个列表状态 pos_diag[i-j+7] = 0 nag_diag[i+j] = 0 if i < 7: do_queen(i+1) #可递增或递减 else: output() #产生一个结果,输出 col[j] = 1 #恢复各个列表状态为之前的 pos_diag[i-j+7] = 1 nag_diag[i+j] = 1 if __name__ == '__main__': col = [] #矩阵列的列表,存储皇后所在列,若该列没有皇后,则相应置为1,反之则0 row = [] #矩阵行的列表,存放每行皇后所在的列位置,随着程序的执行,在不断的变化中,之间输出结果 pos_diag = [] #正对角线,i-j恒定,-7~0~7,并且b(i)+7统一到0~14 nag_diag = [] #负对角线,i+j恒定,0~14 count = 0 for index in range(0, 8): #一些初始化工作 col.append(1) row.append(0) for index in range(0, 15): pos_diag.append(1) nag_diag.append(1) do_queen(0) #开始递归,先放一个,依次递增,反过来,从7开始递减也可 print 'Totally have %d solutions!' % count