题意
好复杂,我就不写了。
题解
口胡了一下,发现我居然会 IOI 的题?
首先发现有 (3) 一定不合法,因为连通块里面有一个环的话 (p_{i,j}) 最多为 (2),有两个环的话就存在一个 (p_{i,j}) 为 (4) 了。
所以每一个连通块之内要么是树要么是基环树。
考虑某个连通块。将这个连通块划分成若干子树,有一个环每个子树的根节点连接起来,比如说下面的图就将它划分为 ({1,2,3},{4,5,6},{7,8,9}) 三棵子树。
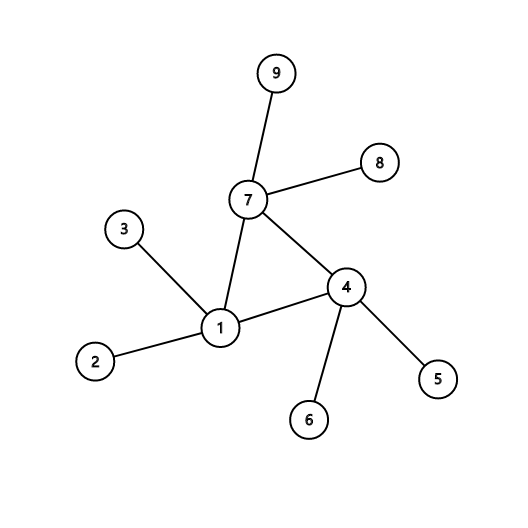
对于在同一个连通块里面的点 (i,j) 来说,如果两个点在一个子树中那么 (p_{i,j}) 显然为 (1),否则 (p_{i,j}=2)。
所以我们可以先将 (p_{i,j}=1) 的那些点合并成子树,再随意指定一个根将所有 (p_{i,j}=2) 的点连成一个环就做完了,这个可以用两个并查集来维护。
这题无解有点难判。
代码
#include<bits/stdc++.h>
#include "supertrees.h"
using namespace std;
typedef int ll;
typedef long long int li;
const ll MAXN=2e3+51;
vector<vector<ll>>res,g,p;
ll n;
ll ffa[MAXN],ffa2[MAXN];
inline ll find(ll x)
{
return x==ffa[x]?x:ffa[x]=find(ffa[x]);
}
inline ll find2(ll x)
{
return x==ffa2[x]?x:ffa2[x]=find(ffa2[x]);
}
inline void connect(ll x,ll y)
{
return (void)(res[x][y]=res[y][x]=1);
}
inline ll merge(ll x,ll y)
{
ll fx=find(x),fy=find(y);
if(fx==fy)
{
return 1;
}
for(register int i=0;i<n;i++)
{
if(p[x][i]!=p[y][i])
{
return 0;
}
}
return connect(fx,fy),ffa[fy]=fx,1;
}
inline void merge2(ll x,ll y)
{
ll fx=find2(x),fy=find2(y);
if(fx!=fy)
{
ffa2[fy]=fx;
}
}
ll construct(vector<vector<ll>>x)
{
p=x,n=p.size(),res.resize(n),g.resize(n);
for(register int i=0;i<n;i++)
{
ffa[i]=ffa2[i]=i,res[i].resize(n);
}
for(register int i=0;i<n;i++)
{
for(register int j=0;j<n;j++)
{
if(p[i][j]>2)
{
return 0;
}
if(i!=j&&p[i][j]==1&&!merge(i,j))
{
return 0;
}
}
}
for(register int i=0;i<n;i++)
{
for(register int j=0;j<n;j++)
{
find(i)==i&&find(j)==j&&p[i][j]==2?merge2(i,j):(void)1;
}
}
for(register int i=0;i<n;i++)
{
for(register int j=0;j<n;j++)
{
if(i!=j&&find(i)==i&&find(j)==j&&find2(i)==find2(j)&&!p[i][j])
{
return 0;
}
}
}
for(register int i=0;i<n;i++)
{
find(i)!=i?connect(i,ffa[i]):g[find2(i)].emplace_back(i);
}
for(register int i=0;i<n;i++)
{
if(find2(i)==i&&g[i].size()==2)
{
return 0;
}
if(find2(i)==i&&g[i].size()>1)
{
for(register int j=0;j<g[i].size();j++)
{
connect(g[i][j],g[i][(j+1)%g[i].size()]);
}
}
}
return build(res),1;
}