3.6 Sharpening (Highpass) Spatial Filters

对于图像的一阶导数与二阶导数定义：

一阶导数：\(\frac{\partial f}{\partial x}=f(x+1)-f(x)\)

二阶导数：\(\frac{\partial ^2f}{\partial x^2}=f(x+1)+f(x-1)-2f(x)\)

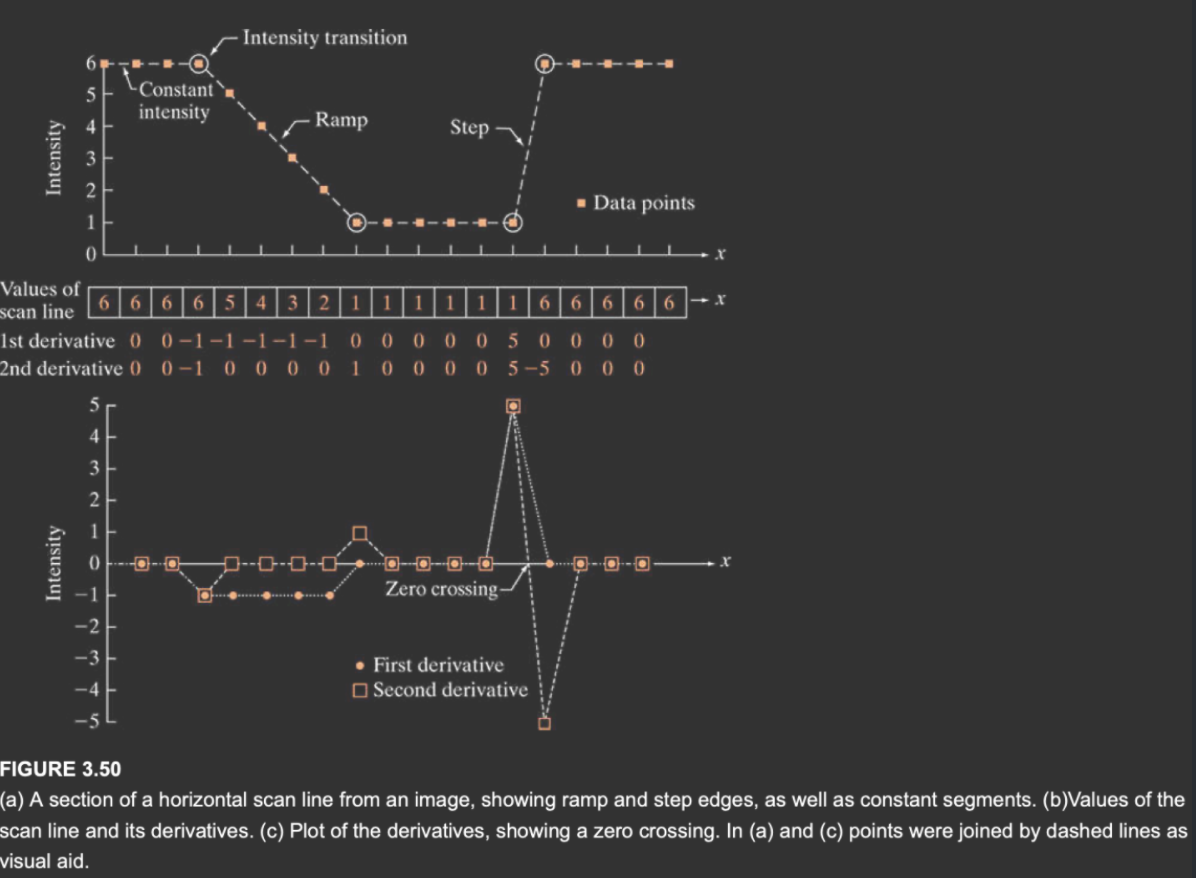
观察上图，二阶导数会在图像的边缘产生正负的跳变，所以二阶导在判断图像的边缘时十分有用。

利用二阶导数对图像进行锐化——拉普拉斯算子

二维下的拉普拉斯算子表示为

\[\nabla^2f(x,y)=\frac{\partial^2f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2} \]

因为是二维函数，所以对上面的定义进行修改：

\[\frac{\partial^2 f}{\partial x^2}=f(x+1,y)+f(x-1,y)-2f(x,y)\\ \frac{\partial^2 f}{\partial y^2}=f(x,y+1)+f(x,y-1)-2f(x,y) \]

代入上式：

\[\nabla^2f(x,y)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) \]

上面的方程可以使用下面的卷积核实现：

生成过程：按照上式每个项的系数（权值）生成卷积系数。

因为拉普拉斯算子是一种导数算子，他会突出图像中的锐利的灰度变化，淡化平滑过渡的部分，这就会产生灰色边缘线和其他的不连续的图像，并且叠加到黑色的、无特征的背景中。通过将进行拉普拉斯变换后的图像添加到原始图像中，可以恢复背景特征，同时还能保持拉普拉斯图像的锐化效果。不过需要注意拉普拉斯算子中心的系数正负。若为负，则需要在原始图像中减去拉普拉斯图像。所以基本的恢复方法为

\[g(x,y)=f(x,y)+c[\nabla^2f(x,y)] \]

Unsharp Masking and Highboost Filtering(反锐化掩膜和高增益滤波)

反锐化掩膜可以用来增强图像的细节。一般包含三步：

1. 模糊原始图像；
2. 从原始图像中减去模糊图像（产生的差值称为遮罩）；
3. 将遮罩添加到原始图像中。

用\(\bar f(x,y)\)表示模糊后的图像，遮罩可以用下式来表示：

\[g_{mask}(x,y)=f(x,y)-\bar f(x,y) \]

然后为遮罩添加权重，加回到原图像中：

\[g(x,y)=f(x,y)+kg_{mask}(x,y) \]

\(k=1\) 则为反锐化掩膜，\(k>1\)则为高增益滤波。\(k<1\)时，可以降低非锐化掩膜的比例。

使用一阶导数来对图像进行锐化——梯度

在点 \(f(x,y)\)处的梯度可以表示为：

\[\nabla f\equiv grad(f)=\left [ \matrix{g_x\\g_y} \right ]= \left[ \matrix{\frac{\partial f}{\partial x}\\ \frac{\partial f}{\partial y}} \right] \]

\(\nabla f\)的长度使用 \(M(x,y)\)来表示：

\[M(x,y)=||\nabla f||=mag(\nabla f)=\sqrt{g_x^2+g_y^2} \]

其中，M(x,y)与原图像同样大小，这幅图像通常被称为渐变图。

有时候用L0 范数：

\[M(x,y)\approx |g_x|+|g_y| \]

由于图像都是离散值，我们定义以下符号：

如在一个\(3\times 3\)的图像中，\(z_5\)表示 \(f(x,y)\)，\(z_1\)表示 \(f(x-1,y-1)\)。定义 \(g_x=(z_9-z_5),g_y=(z_8-z_6)\)。（Roberts cross-gradient operators）

\[M(x,y)=[(z_9-z_5)^2-(z_8-z_6)^2]^{1/2}\\ M(x,y)\approx |z_9-z_5|+|z_8-z_6| \]

这个操作可以使用下面的核来实现：

但是我们使用的核大小一般为奇数，对于一个\(3\times 3\)大小的核：

\[g_x=\frac{\partial f}{\partial x}=(z_7+2z_8+z_9)-(z_1+2z_2+z_3)\\ g_y=\frac{\partial f}{\partial y}=(z_3+2z_6+z_9)-(z_1+2z_4+z_7) \]

上式可以用下面的核来实现：

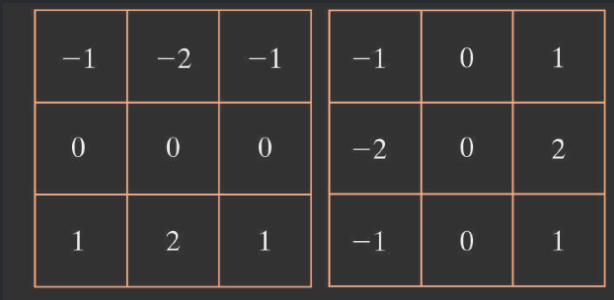
通过将图像中所有的点与这个核进行卷积，可以得到所有点的偏导数。

\[M(x,y)=[g_x^2+g_y^2]^{1/2}[[(z_7+2z_8+z_9)-(z_1+2z_2+z_3)]^2+[(z_3+2z_6+z_9)-(z_1+2z_4+z_7)]^2]^{1/2} \]

这个式子表明，任意点(x,y)处的 M 值是通过将两个核与图像进行卷积，平方后相加再开方得出的。

这个核叫做 Sobel 算子。在中心处使用 2 为系数的意图是，对中心店多一些重视而实现平滑。这个核的系数之和为 0，因此这些核在一个恒定灰度值区域的卷积恒为 0，这样就不会产生偏差。