平滑(平均)空间滤波器用来减少灰度值的急剧变化。由于随机噪声通常是由灰度值的急剧变化产生的,所以平滑处理的一个最大的用处就是用来降噪。另一个应用是用来平滑在图像中由于亮度级别不足而产生的假轮廓。
线性空间滤波包括使用滤波器核卷积图像。将平滑核与图像卷积可以让图像变得模糊,模糊的称呼由核的大小以及系数决定。同时,低通滤波器可以派生出锐化(高通滤波器)、带通、带阻滤波器等等。
Box Filter Kernels(盒式滤波器)
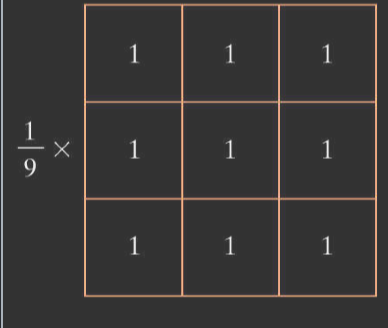
盒式滤波器是最简单的滤波器之一,滤波器的所有值都为一个相同的数(通常为 1)。还需要对其进行标准化,也就是下面的\(\frac{1}{9}\)。

Lowpass Gaussian Filter Kernels
对于有的应用,盒式过滤器还是不能胜任的,比如散焦透镜通常被建模为低通滤波器,但是盒式滤波器对透镜的模糊特性的模拟较差;另外,盒式过滤器有利于沿着垂直方向模糊,在涉及到具有高细节级别的图像或者具有强几何分量图像的应用上,盒式过滤器效果通常并不好。
对于上面提到的两种情况,通常使用圆对称(circularly symmetric),也叫做各向同性。形式如下:
由于在这里感兴趣的只是高斯函数的钟形曲线,所以前面的系数使用 \(K\)来代替。
\(s\) 和 \(t\) 是坐标,坐标原点为核中心。
高斯函数是唯一一个可分离的圆对称核。所以高斯核与盒式滤波器有着相同的计算优势,但是其有许多其他属性。
令 \(r=[s^2+t^2]^{1/2}\),上式可以写为
\(r\)是从中心到函数 \(G\)上任意点的距离。
下面是高斯函数的透视图:
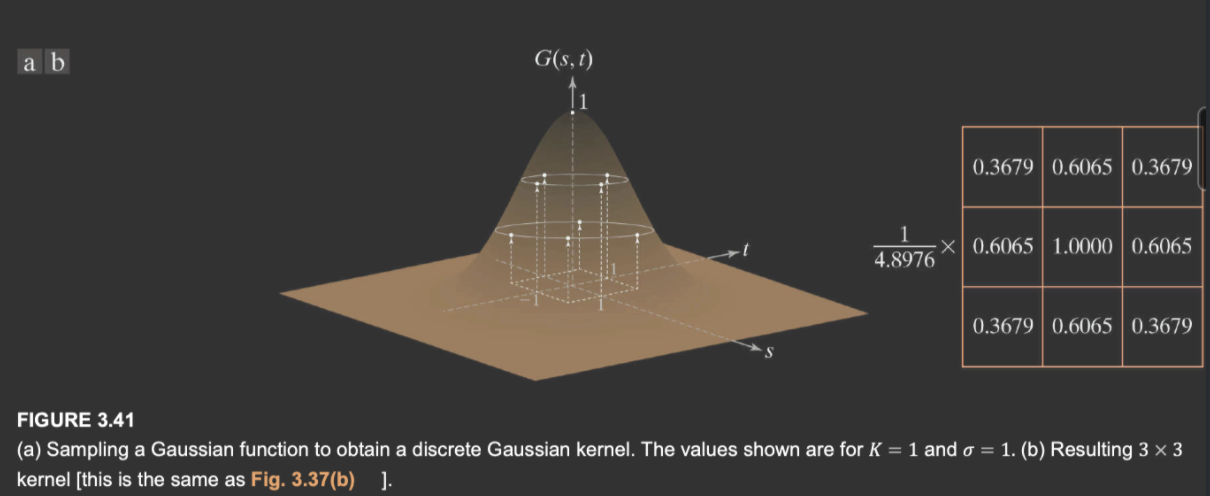
回想一下高斯函数的钟形曲线。在距离平均值\(3\sigma\)之外的概率可以忽略不计。也就是说,如果我们选择一个\(\lceil6\sigma\rceil \times \lceil 6\sigma\rceil\)大小的高斯核,就能与使用更大的高斯核得到差不多的结果。换个角度看,使用比原图像更大的高斯核不会得到任何结果。所以一般来说,我们使用满足这个条件的最小整数,比如 \(43\times 43\)的核,\(\sigma=7\)。
高斯函数的另外两个基本性质是:两个高斯函数的乘积与卷积都是高斯函数。我们上面使用的高斯函数的平均值都是 0,所以我们关注的是标准偏差。
| f | g | \(f\times g\) | \(f★g\) | |
|---|---|---|---|---|
| 平均值 | \(m_f\) | \(m_g\) | \(m_{f\times g}=\frac{m_f\sigma_g^2+m_g\sigma_f^2}{\sigma_f^2+\sigma_g^2}\) | \(m_{f★g}=m_f+m_g\) |
| 标准差 | \(\sigma_f\) | \(\sigma_g\) | \(\sigma_{f\times g}=\sqrt{\frac{\sigma_f^2\sigma_g^2}{\sigma_f^2+\sigma_g^2}}\) | \(\sigma_{f★g}=\sqrt{\sigma_f^2+\sigma_g^2}\) |
当我们需要进行一系列的高斯卷积时,就可以应用上面的结论,计算多个高斯核的复合标准差,而不需要实际去执行所有单核的卷积。
一些例子
下图中,中是经过盒式滤波器处理后的图形,右是经过高斯滤波器处理后的图形。两者相比,盒式滤波器对于边缘的处理不如高斯平滑。所以如果有较少的边缘平滑时,我们可以使用盒式滤波器;如果需要均匀平滑时,使用高斯滤波器。

关于填充
通过零填充的方法填充图像边界,会导致图像处理后出现黑边。
镜像填充(对称填充):以图像边界为轴,镜像图像的边界。当图像附近的区域包含图像的细节时,镜像填充比较适合。
复制填充:将图像边界外的部分复制为最近的图像边界,这种方法对于图像边界附近的区域保持不变时很有用。
Order-Statistic(Nonlinear) Filters(顺序统计滤波器)
顺序统计滤波器将在一个区域中的像素进行排序,通过排序结果确定的值,去替换中心像素的值来实现平滑。这一类滤波器中最著名的滤波器是中值滤波器。顾名思义,中值滤波器将中心点的值替换为该像素点附近灰度值的中值(计算中值时包括中心点)。中值滤波器为某些类型的随机噪声提供了出色的降噪能力,与类似大小的线性滤波器相比,模糊程度要小很多。中值滤波器在存在脉冲噪声(椒盐噪声,一种随机出现的黑白点)是特别有效。