靠二进制画几何[图论]

@Kaike

今天来浅谈一下图，听说自己写总结的人grade++，rp++。

像我这样可爱的人怎么能错过这个机会呢嘤嘤嘤。

毕竟图至少啃了15day++。

恩曾经的小弱渣从来都是仰望高端玩家虐图论

听说noip上一年考两道大图(つд⊂)而小弱渣还没学到

吓得本宝宝虎躯一震！！

恩废话不多说，来开正文。

2019/01/27：

时隔两年重新看这篇博客，又更新的好多东西，希望自己一直能不断进步把，而不是一直啃以前的东西QAQ

-------------------我是萌哒哒的分割线--------------------

刚开始先学图的储存。

1. 邻接矩阵

邻接矩阵就是跟二维数组长得一毛（mu）一样奇奇怪怪的东xi

#include<iostream>
using namespace std;
int n,a[100][100];
int main()
{
    cin>>n;
    //直接给出邻接矩阵，直接读。
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            cin>>a[i][j];
    //给出两个顶点和权值
    for(int i=1;i<=n;i++)
    {
        int xx,yy,vv;
        cin>>xx>>yy>>vv;
        a[xx][yy]=vv;
        //双向图时
        a[yy][xx]=vv;
    }
    //给出每个顶点的临界点
    for(int i=1;i<=n;i++)
    {
        int k;
        cin>>k;
        for(int j=1;j<=k;j++)
        {
            int x;
            cin>>x;
            a[i][x]=1;
            a[x][i]=1;
        }
    }
    return 0;
}

2.邻接表

第一次看这玩意的时候内心万般草泥马奔过。

这TM都是什么玩意

后来经过滑稽大师cdc柴大叔的指导下，莫名其妙知道了些什么

然而教材太过简单，时常还会有些错的

小弱渣花了一整节自习课照着书上画了一幅图，发现！原来！跟书上一毛（mu）一样。本宝宝不开心，哦是十分不开心。

这大概是这个样子的

#include<iostream>
using namespace std;
int n;
int link[10010],len=0;
struct ha
{
    int y,v,next;
}e[10010];
void insert(int xx,int yy,int vv)
{
    e[++len].next=link[xx];
    link[xx]=len;
    e[len].y=yy;
    e[len].v=vv;
}
int main()
{
    cin>>n;
    int xx,yy,vv;
    for(int i=1;i<=n;i++)
    {
        cin>>xx>>yy>>vv;
        insert(xx,yy,vv);
        insert(yy,xx,vv);
    }
    return 0;
}

如果出现重边！邻接矩阵必须判断！！

-----------------我是萌萌哒的分割线------------------

DFS：以一个未被访问过的顶点作为起始顶点，沿当前顶点的边走到未访问过的顶点；当没有未访问过的顶点时，则回到上一个顶点，继续试探访问别的顶点，直到所有的顶点都被访问过。

#include<iostream>
using namespace std;
bool book[10010];//记录顶点是否被访问过
int a[10010][10010],n,m;
int inf=0x7fffffff;
int sum=0;
//邻接矩阵
void dfs(int x)
{
    for(int i=1;i<=n;i++)
        if(book[i]==0 && a[x][i])
        {
            book[i]=1;
            dfs(i);
        }
}
//邻接表
void dfs(int x)
{
    for(int i=link[x];i;i=e[i].next)
        if(book[e[i].y]==0)
        {
            book[e[i].y]=1;
            dfs(e[i].y);
        }
}
int main()
{
    cin>>n;
    //初始化
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(i==j)    a[i][j]=0;
            else    a[i][j]=inf;
    int xx,yy,vv;
    for(int i=1;i<=m;i++)
    {
        cin>>xx>>yy>>vv;
        a[xx][yy]=vv;
        a[yy][xx]=vv;
    }
    for(int i=1;i<=n;i++)
        if(book[i]==0)
        {
            //求无向图的连接分量
            sum++;
            dfs(i);
        }
    return 0;
}

BFS：以一个未被访问过的顶点作为起始顶点，访问其所有相邻的顶点，然后对每个相邻的顶点，在访问它们相邻的未被访问过的顶点，直到所有顶点都被访问过。

#include<iostream>
using namespace std;
bool book[10010];//记录顶点是否被访问过
int a[10010][10010],n,m;
int inf=0x7fffffff;
int sum=0;
int q[10010];//队列，数组一定要开大！！
//邻接矩阵
void bfs(int x)
{
    int head=0,tail=1;
    q[1]=x;
    book[i]=1;
    while(head<tail)
    {
        int k=q[++head];
        for(int i=1;i<=n;i++)
            if(a[x][i] &&book[i]==0)
            {
                q[++tail]=i;
                book[i]=1;
            }
    }
}
//邻接表
void dfs(int x)
{
    int head=0,tail=1;
    q[1]=x;
    while(head<tail)
    {
        for(int i=link[q[head]];i;i=e[i].next)
            if(book[e[i].y]==0)
            {
                book[e[i].y]=1;
                q[++tail]=e[i].y;
            }
    }
}
int main()
{
    cin>>n;
    //初始化
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(i==j)    a[i][j]=0;
            else    a[i][j]=inf;
    int xx,yy,vv;
    for(int i=1;i<=m;i++)
    {
        cin>>xx>>yy>>vv;
        a[xx][yy]=vv;
        a[yy][xx]=vv;
    }
    for(int i=1;i<=n;i++)
        if(book[i]==0)
        {
            //求无向图的连接分量
            sum++;
            dfs(i);
        }
    return 0;
}

 

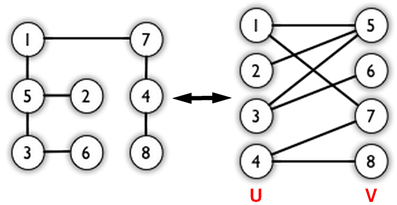
Bicoloring

传送门

这道题就是用bfs遍历一遍，用两种颜色来填充顶点，有边相邻的顶点颜色不能一样，邻接矩阵很好写，很好判断两个点，可是空间太大了。

邻接表想了好久，最终确定了两个顶点分别是 q[head] 和 e[i].y  i=Link[q[head]] 

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<map>
#include<set>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
const int N = 200 + 20;
int a[N][N];
int cor[N];
int n, m,flag=1,xx,yy;
void dfs(int x)
{
    for (int i = 0; i < n; i++)
    {
        if (a[x][i] && cor[i] == 0)
        {
            if (cor[x] == 1)
                cor[i] = 2;
            else cor[i] = 1;
            dfs(i);
        }
        else if (cor[i] == cor[x] &&a[x][i])
        {
            flag = 0;
            return;
        }
    }
}
int main()
{
    while (scanf("%d", &n))
    {
        if (n == 0)    break;
        memset(a, 0, sizeof(a));
        memset(cor, 0, sizeof(cor));
        flag = 1;
        scanf("%d",&m);
        while (m--)
        {
            scanf("%d %d",&xx,&yy);
            a[xx][yy] = 1;
            a[yy][xx] = 1;
        }
        cor[0] = 1;
        dfs(0);
        if (flag == 0)    printf("NOT BICOLORABLE.
");
        else printf("BICOLORABLE.
");
    }

    return 0;
}

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
const int N = 100000 + 20;
int Link[N],cor[N],len=0,bok[N];
int n, m;
int q[N];
struct student
{
    int y, next;
}e[N];
void insert(int xx, int yy)
{
    e[++len].next = Link[xx];
    Link[xx] = len;
    e[len].y = yy;
}
int bfs(int x)
{
    int head = 1, tail = 2;
    q[1] = x;
    bok[x] = 1;
    cor[x] = 1;
    while (head < tail)
    {
        for (int i = Link[q[head]]; i; i = e[i].next)
        {
            if (cor[e[i].y] == 0)
            {
                if (cor[q[head]] == 1)
                    cor[e[i].y] = 2;
                else
                    cor[e[i].y] = 1;
            }
            else if (cor[e[i].y] == cor[q[head]])
                return 0;
            if (bok[e[i].y] == 0)
            {
                bok[e[i].y] = 1;
                q[tail++] = e[i].y;
            }
        }
        head++;
    }
    return 1;
}
int main()
{
    while (scanf("%d", &n))
    {
        memset(bok, 0, sizeof(bok));
        memset(Link, 0, sizeof(Link));
        memset(q, 0, sizeof(q));
        memset(cor, 0, sizeof(cor));
        if (n == 0)    break;
        scanf("%d", &m);
        while (m--)
        {
            int xx, yy;
            scanf("%d %d", &xx, &yy);
            insert(xx, yy);
            insert(yy, xx);
        }
        if (bfs(0))    printf("BICOLORABLE.
");
        else printf("NOT BICOLORABLE.
");
    }
    return 0;
}

拓扑排序：

拓扑就是类似于游戏中点技能，只有先把低级技能点了，才能点高阶技能。一个低阶技能可能对应多个高阶技能，高阶技能本身也可以互相对应。

那我们怎么办呢，另开一个数组indu，表示入度。

刚开始先找入度为0的点，从这个点开始遍历，然后再找，入度为1的点，再往下找入度为2的点。

每次找到一个，就减去它的入度，相当于把前面那个点删除掉，相应的边也删除掉。

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
const int N = 10000;
int Link[110], bok[110],len=0,indu[110],que[N];
int n, m, xx, yy;
struct student
{
    int y, next;
}e[N];
void insert(int xx, int yy)
{
    e[++len].next = Link[xx];
    Link[xx] = len;
    e[len].y = yy;
}
void bfs()
{
    int head = 1, tail = 1;
    for (int i = 1; i <= n; i++)
        if (indu[i] == 0)
        {
            que[tail++] = i;
            bok[i] = 1;
        }
    while (head < tail)
    {
        for (int i = Link[que[head]]; i; i = e[i].next)
        {
            if (--indu[e[i].y] == 0 && bok[e[i].y] == 0)
            {
                que[tail++] = e[i].y;
                bok[e[i].y] = 1;
            }
        }
        head++;
    }
    printf("%d",que[1]);
    for (int i = 2; i <=n; i++)
        printf(" %d",que[i]);
    printf("
");
}
int main()
{
    while (scanf("%d %d",&n,&m))
    {
        if (n == 0)    break;
        memset(e, 0, sizeof(e));
        memset(Link, 0, sizeof(Link));
        memset(que, 0, sizeof(que));
        memset(bok, 0, sizeof(bok));
        memset(indu, 0, sizeof(indu));
        while (m--)
        {
            scanf("%d %d", &xx, &yy);
            insert(xx, yy);
            indu[yy]++;
        }
        bfs();
    }
    return 0;
}

（他们全都用的stl的vector，我用的邻接表啊，高端东西，没有资料全靠自己创。好难过。）

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<algorithm>
#include<cmath>
using namespace std;
#define ll long long
const int N = 12500 + 10;
priority_queue<int, vector<int>, greater<int> >q;
int Link[510], bok[510],a[510],len=0,indu[510],cnt=0;
int n, m, xx, yy;
int ans = 0;
struct student
{
    int y, next;
}e[N];
void insert(int xx, int yy)
{
    e[++len].next = Link[xx];
    Link[xx] = len;
    e[len].y = yy;
}
void bfs()
{
    cnt = 0;
    ans = 0;
    for(int i=1;i<=n;i++)
        if (indu[i] == 0)
        {
            bok[i] = 1;
            q.push(i);
            //cout << i << endl;
        }
    //cout << endl;
    while (!q.empty())
    {
        //a[++cnt] = q.top();
        int tt = q.top();
        q.pop();
        ans++;
        if (ans == 1)
            printf("%d",tt);
        else printf(" %d",tt);
        for (int i = Link[tt]; i; i = e[i].next)
        {
            if (--indu[e[i].y] == 0 && bok[e[i].y] == 0)
            {
                q.push(e[i].y);
                bok[e[i].y] = 1;
            }
        }
    }
    printf("
");
}
int main()
{
    while (scanf("%d %d", &n, &m) != EOF)
    {
        memset(Link, 0, sizeof(Link));
        memset(bok, 0, sizeof(bok));
        memset(e, 0, sizeof(e));
        memset(a, 0, sizeof(a));
        memset(indu, 0, sizeof(indu));
        len = 0;
        while (m--)
        {
            scanf("%d %d",&xx,&yy);
            indu[yy]++;
            insert(xx, yy);
        }
        bfs();
    }

    return 0;
}

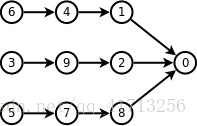
举个例子如图：

如果你用优先队列拓扑排序得到的是：3 5 6 4 1 7 8 9 2 0

但是正确答案为 6 4 1 3 9 2 5 7 8 0 这样使得小的（1）尽量在前面。

优先队列是让数字整体小的在前面，而编号最小是让1尽量在前面，这两者是不同的，想了好久才知道QAQ。

#include "pch.h"
#pragma warning(disable:4996)
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<algorithm>
#include<cmath>
using namespace std;
#define ll long long
const int N = 100000 + 10;
priority_queue<int, vector<int>, less<int> >q;
int Link[30010], bok[30010],a[30010],len=0,indu[30010],cnt=0;
int n, m, xx, yy;
int ans = 0;
struct student
{
    int y, next;
}e[N];
void insert(int xx, int yy)
{
    e[++len].next = Link[xx];
    Link[xx] = len;
    e[len].y = yy;
}
void bfs()
{
    cnt = 0;
    ans = 0;
    for(int i=1;i<=n;i++)
        if (indu[i] == 0)
        {
            bok[i] = 1;
            q.push(i);
            //cout << i << endl;
        }
    //cout << endl;
    while (!q.empty())
    {
        //a[++cnt] = q.top();
        int tt = q.top();
        q.pop();
        a[++ans] = tt;
        for (int i = Link[tt]; i; i = e[i].next)
        {
            if (--indu[e[i].y] == 0 && bok[e[i].y] == 0)
            {
                q.push(e[i].y);
                bok[e[i].y] = 1;
            }
        }
    }
    for (int i = ans; i >= 1; i--)
    {
        if (i == ans)
            printf("%d",a[i]);
        else printf(" %d",a[i]);
    }
    printf("
");
}
int main()
{
    int t;
    scanf("%d",&t);
    while (t--)
    {
        scanf("%d %d", &n, &m);
        memset(Link, 0, sizeof(Link));
        memset(bok, 0, sizeof(bok));
        memset(e, 0, sizeof(e));
        memset(a, 0, sizeof(a));
        memset(indu, 0, sizeof(indu));
        len = 0;
        while (m--)
        {
            scanf("%d %d",&xx,&yy);
            indu[xx]++;
            insert(yy, xx);
        }
        bfs();
    }

    return 0;
}

还搞了搞优先队列

priority_queue <int,vector<int>,greater<int> > q;
priority_queue <int,vector<int>,less<int> >q;

欧拉回路：

欧拉回路是指不令笔离开纸面，可画过图中每条边仅一次，且可以回到起点的一条回路。现给定一个图，问是否存在欧拉回路？

如何判断欧拉回路呢：首先它是连通图，其次对于无向图来说，所有顶点度数为偶数。

判断联通可以用并查集，判断度数很好写。

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<algorithm>
#include<cmath>
using namespace std;
#define ll long long
const int N = 1010;
int a[N][N],indu[N],par[N];
int n, m, xx, yy;
int find(int x)
{
    if (par[x] == x)    return x;
    return par[x] = find(par[x]);
}
void hebing(int a, int b)
{
    a = find(a);
    b = find(b);
    if (a != b)
        par[a] = b;
}
int main()
{
    while (scanf("%d", &n))
    {
        if (n == 0)    break;
        scanf("%d", &m);
        memset(a, 0, sizeof(a));
        memset(indu, 0, sizeof(indu));
        for (int i = 1; i <= n; i++)
            par[i] = i;
        while (m--)
        {
            scanf("%d %d", &xx, &yy);
            indu[xx]++;
            indu[yy]++;
            hebing(xx, yy);
        }
        int cnt = 0;
        for (int i = 1; i <= n; i++)
            if (par[i] == i)
                cnt++;
        if (cnt > 1)
        {
            printf("0
");
            continue;
        }
        cnt = 0;
        for (int i = 1; i <= n; i++)
            if (indu[i] % 2 == 1)
                cnt++;
        if (cnt > 0)
            printf("0
");
        else printf("1
");
    }

    return 0;
}

输出欧拉回路：

就是从一个顶点起，一笔走过所有的边。dfs遍历边！

以前的dfs和bfs都是遍历顶点，而这个是遍历边！

这个只能用dfs，我想了想因为你一笔走的就是一个dfs的过程，不存在bfs的过程，如果有bfs的话，那就画一条回去，在画另一条。跟题意不否。

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<algorithm>
#include<cmath>
using namespace std;
#define ll long long
const int N =10010;
const int M = 50000 + 100;
int Link[N],bok[N],len=0,q[N];
int n, m, xx, yy;
struct student
{
    int y, next,vis;
}e[M*2];
void insert(int xx, int yy)
{
    e[++len].next = Link[xx];
    Link[xx] = len;
    e[len].y = yy;
    e[len].vis = 0;
}
void init()
{
    scanf("%d %d",&n,&m);
    while (m--)
    {
        scanf("%d %d",&xx,&yy);
        insert(xx, yy);
        insert(yy, xx);
    }
}
void dfs(int x)
{
    for(int i=Link[x];i;i=e[i].next)
        if (e[i].vis == 0)
        {
            e[i].vis = 1;
            dfs(e[i].y);
        }
    printf("%d
",x);
}
int main()
{
    init();
    dfs(1);
    return 0;
}

判断欧拉回路的个数：

传送门

对于每个以i为根的连通分量我们记录属于该连通分量的点数目num[i]和该连通分量中奇度点的个数odd[i].
如果num[i]==0或1,需0笔.(注意num[i]==0表示i点不是根,num[i]==1表示i点是一个孤立的点.)
如果num[i]>1且odd[i]==0 需1笔
如果num[i]>1且odd[i]>0 需odd[i]/2笔

1205.田野上的环

传送门

刚开始的时候小弱渣刚刚理解什么是邻接矩阵，对于dfs还不熟

然而现在看书上 邻接矩阵+dfs 简直扯淡

总而言之这道题就是找与1不相连的点

dfs 两个变量 用（1，i）来遍历；

找与1相连，然后依次递归

最后看谁还没有遍历，按顺序输出

最后用布尔判断 是不是没有！

#include<iostream>
using namespace std;
int a[300][300],n,m,x,y;
bool b=0,f[300];
void dfs(int x,int y)
{
    if(a[x][y]==1&&f[y]!=1)
    {
        f[y]=1;
        for(int i=1;i<=n;i++)
            dfs(y,i);
    }
    else    return;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>x>>y;
        a[x][y]=1;
        a[y][x]=1;
    }
    for(int i=1;i<=n;i++)
        a[i][i]=1;
    for(int i=2;i<=n;i++)
        dfs(1,i);
    for(int i=2;i<=n;i++)
        if(f[i]==0)
        {   b=1;
            cout<<i<<endl;
        }
    if(b==0)    cout<<0<<endl;
    return 0;
}

1206.1207.1208.犯罪集团

传送门

就是找几个连通分量，注意数组开大，小弱渣卡了好几次。

#include<iostream>
#include<cstring>
using namespace std;
int n,m,x,y,len=0;
int link[50100],ans=0,q[50100];
bool f[50100];
struct edge
{
    int y,next;
}e[50100];
void in(int xx,int yy)
{
    e[++len].next=link[xx];
    link[xx]=len;
    e[len].y=yy;
}
void bfs(int k)
{
    memset(q,0,sizeof(q));
    int head=0,tail=1;
    q[1]=k;
    while(head++<tail)
        for(int i=link[q[head]];i;i=e[i].next)
            if(!f[e[i].y])
            {
                f[e[i].y]=1;
                q[++tail]=e[i].y;
            }
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>x>>y;
        in(x,y);
        in(y,x);
    }
    for(int i=1;i<=n;i++)
        if(!f[i])
        {
            ans++;
            bfs(i);
        }
    cout<<ans<<endl;
    return 0;
}

 

1210.骑马修栅栏

传送门

书上写着欧拉路与欧拉回路，把求最小路都做出来了死活还都不知道欧拉路是什么鬼

嗯去科技馆的时候好像看过一个叫欧拉路的玩意

然而跟题目有毛关系（怒拍桌子！）

啊因为不会欧拉路，so现在看这道题还是不会

你看这个人怎么这么懒。没办法你来打我啊

算了我们还是跳过这道题吧

/*
by kaike
11/15/2016
*/
//这题是让求出一条欧拉路。
#include<iostream>
using namespace std;
int xx,yy,m;
int l[1028][1028],du[1028],maxx=0;
int a[1028],t=0;
//找到和它相连的，依次删除他们之间的连线。
//再找新的点，最后把这个点加入输出队列。
void find(int k)
{
    for(int i=1;i<=maxx;i++)
        if(l[k][i])
        {
            l[k][i]--;
            l[i][k]--;
            find(i);
        }
    a[++t]=k;
}
int main()
{
    cin>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>xx>>yy;
        l[xx][yy]++;    
        l[yy][xx]++;
        du[xx]++;
        du[yy]++;
        if(xx>maxx) maxx=xx;
        if(yy>maxx) maxx=yy;
    }
    int s=1;
//数据保证至少有1个解，那就一定存在欧拉路。
//我们要选一个点为起点，要在字典序中找出最小的，就要找最小的点为起点。
    for(int i=1;i<=maxx;i++)
        if(du[i]%2==1)
        {
            s=i;
            break;
        }
//对于当前的点，把所有点从小到大搜索。
    find(s);
//这样做之后，顺序是反着的。
    for(int i=m+1;i>0;i--)
        cout<<a[i]<<endl;
    return 0;
}

 

1209.几何图形还原

传送门

这道题需要多注意！多注意！多注意！

因为还需要回溯啊

Why？

害怕这条路走不通，换一条路试试咯

所有的边都连起来了，就说明最后一个顶点跟1顶点肯定是连起来的

因为要输出字典序最小的那个，所以只要从1开始遍历就哦可，算是个隐藏的小细节

dfs 每遍历一个点就用数组记录下来，然后继续遍历

回溯。

最后判断最后一个点跟1是否相连，相连输出退出。

#include<iostream>
#include<stdlib.h>
using namespace std;
int n,ans[60],t=1;
int a[60][60],xx,yy;
int f[60];
bool book[60];
void dfs(int k)
{
    if(t==n)
    {
        if(f[ans[t]]!=1)    return;
        else
        {    for(int i=1;i<=n;i++)
                cout<<ans[i]<<' ';
            exit(0);
        }
    }
    for(int i=1;i<=n;i++)
        if(a[k][i]==1&& book[i]==0)
        {
            book[i]=1;
            ans[++t]=i;
            dfs(i);
            book[i]=0;
            t--;
        }
}
int main()
{
    cin>>n;
    while(cin>>xx>>yy)
    {
        a[xx][yy]=1;
        a[yy][xx]=1;
    }
    for(int i=1;i<=n;i++)
        f[i]=a[i][1];
    book[1]=1;
    ans[1]=1;
    dfs(1);
    return 0;
}

 

1211.街道赛跑

传送门

题太复杂，看题解都看不懂，回来写。

这里这里

--------------------我是萌萌哒的分割线---------------

嗯真开心，终于要到最短路了。

累了本宝宝了。

1212. Geodetic集合

传送门

这应该是一个求最短路的吧，然而教材上写图的传递闭包，什么鬼

就是求从 i-j 最短路中可能经过的点 顺序输出。

要多注意！多注意！多注意！

先用 floyed 求出每个点的最短路

然后依次枚举，如果最短路相同 用三维数组存起来点

然后输出

#include<iostream>
#include<algorithm>
using namespace std;
int a[50][50],b[50][50][50],c[50][50];
int n,m,q;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(i==j)    a[i][j]=0;
            else    a[i][j]=100;
    int xx,yy;
    for(int i=1;i<=m;i++)
    {
        cin>>xx>>yy;
        a[xx][yy]=1;
        a[yy][xx]=1;
    }
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                if(a[i][j]>a[i][k]+a[k][j])
                    a[i][j]=a[i][k]+a[k][j];
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                if(a[i][j]==a[i][k]+a[k][j] && k!=i && k!=j && i!=j )
                    b[i][j][c[i][j]++]=k;
    cin>>q;
    int x,y;
    for(int i=1;i<=q;i++)
    {
        cin>>x>>y;
        b[x][y][c[x][y]++]=x;
        b[x][y][c[x][y]++]=y;
        sort(b[x][y],b[x][y]+c[x][y]+1);
        for(int j=1;j<=c[x][y];j++)
            cout<<b[x][y][j]<<' ';
        cout<<endl;
    }
    return 0;
}

FLOYED

就是找中间点看是否可以松弛，适用于连接矩阵。

for(int k=1;k<=n;k++)
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(a[i][j]>a[i][k]+a[k][j])
                a[i][j]=a[i][k]+a[k][j];

1213.最优乘车

传送门

直接floyed 然后输出 a[1][n]-1

#include<iostream>
#include<cstdio>
using namespace std;
int a[510][510],n,m,t[510],l;
char c;
int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(i==j)    a[i][j]=0;
            else    a[i][j]=1000;
    for(int i=1;i<=m;i++)
    {
        c=' ';
        l=0;
        while(c!=10)
        {
            cin>>t[++l];
            c=getchar();
        }
        for(int j=1;j<l;j++)
            for(int k=j+1;k<=l;k++)
                a[t[j]][t[k]]=1;
    }
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                if(a[i][j]>a[i][k]+a[k][j])
                    a[i][j]=a[i][k]+a[k][j];
    if((a[1][n]==1000)||(a[1][n]==0))  cout<<"NO"<<endl;
    else    cout<<a[1][n]-1<<endl;
    return 0;
}

1214. Bessie Come Home

传送门

这道题最大的坑点就是有a-Z 个粮仓

然后把字符转换为数字，floyed

从大写字母中找去粮仓最小的路程 输出，并输出 i；

#include<iostream>
#include<stdio.h>
#include<string.h>
#define MAX 0xfffffff
using namespace std;
int p,m[55][55],w[55],t,minnum=MAX;
char t1,t2,ans;
char ch(char t)
{
    if(isupper(t))
    {
        t=t-'A'+26;
        w[t]=1;
        return t;
    }
    return t-'a';
}
int main(void)
{
    cin>>p;
    memset(m,-1,sizeof(m));
    for(int i=0;i<52;i++)
        m[i][i]=0; 
    for(int i=0;i<p;i++)
    {
        cin>>t1>>t2>>t;
        t1=ch(t1);
        t2=ch(t2);
        if(m[t1][t2]==-1 || m[t1][t2]>t)
        {
            m[t1][t2]=t;
            m[t2][t1]=t;
        }
    }
    for(int i=0;i<55;i++)
        for(int j=0;j<55;j++)
            for(int k=0;k<55;k++)
                if(m[i][k]!=-1 && m[j][k]!=-1)
                    if(m[i][j]==-1 || (m[j][k]+m[i][k]<m[i][j]))
                        m[i][j]=m[j][k]+m[i][k];
    for(int i=26;i<51;i++)
        if(w[i] && m[i][51]<minnum)
        {
            minnum=m[i][51];
            ans=(char)(i-26+'A');
        }
    cout<<ans<<' '<<minnum<<endl;
    return 0;
}

DIJKSTRA

这是求指定一个点到其余各个顶点的最短路径

（单源 非负）

用book 数组标记

用 dis 数组标记距离

找出离 1 最近的点，然后依次松弛 floyed

#include<iostream>
using namespace std;
int a[10010][10010],dis[10010];
bool book[10010];
int inf=0x7fffffff;
int minn=inf;
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(i==j)    a[i][j]=0;
            else    a[i][j]=inf;
    int xx,yy,vv;
    for(int i=1;i<=m;i++)
    {
        cin>>xx>>yy>>vv;
        a[xx][yy]=vv;
        //a[yy][xx]=vv;
    }
    for(int i=1;i<=n;i++)
    {   dis[i]=a[1][i];
        book[i]=0;
    }
    book[1]=1;
    int u;
    //dijkstra
    for(int i=1;i<=n;i++)
    {
        minn=inf;
        for(int j=1;j<=n;j++)
            if(book[j]==0 && dis[j]<minn )
            {
                minn=dis[j];
                u=j;
            }
        book[u]=1;
        for(int j=1;j<=n;j++)
            if(a[u][j]<inf)
                if(dis[j]>dis[u]+a[u][j])
                    dis[j]=dis[u]+a[u][j];
    }
    for(int i=1;i<=n;i++)
        cout<<dis[i]<<endl;
    return 0;
}

邻接表：

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
const int inf=0x7fffffff;
const int N=200+10;
const int M=20000;
int n,m,xx,yy,vv;
int Link[N],len=0,bok[N],dis[N];
struct student
{
    int y,v,next;
}e[M];
void insert(int xx,int yy,int vv)
{
    e[++len].next=Link[xx];
    Link[xx]=len;
    e[len].y=yy;
    e[len].v=vv;
}
void init()
{
    scanf("%d %d",&n,&m);
    while(m--)
    {
        scanf("%d %d %d",&xx,&yy,&vv);
        insert(xx,yy,vv);
    }
}
void print()
{
    for(int i=1;i<=n;i++)
        printf("%d ",dis[i]);
    printf("
");
}
void dijkstra()
{
    bok[1]=1;
    int u;
    for(int i=2;i<=n;i++)
        dis[i]=inf;
    for(int i=Link[1];i;i=e[i].next)
        dis[e[i].y]=e[i].v;
    for(int i=1;i<n;i++)
    {
        int minn=inf;
        for(int j=1;j<=n;j++)
            if(bok[j]==0&&dis[j]<minn)
            {
                minn=dis[j];
                u=j;
            }
        bok[u]=1;
        for(int i=Link[u];i;i=e[i].next)
        {
            if(dis[e[i].y]>dis[u]+e[i].v)
                dis[e[i].y]=dis[u]+e[i].v;
        }
    }
}
int main()
{
    init();
    dijkstra();
    print();
    return 0;
}

DIJKSTRA：

1.找出最近的那个点

2.更新

1217.晚餐

传送门

就是dijkstra ，然后求距离小于 t 的有几个

#include<iostream>
using namespace std;
int t,f,p,ans=0;
int a[550][550],dis[550];
bool book[550];
int main()
{
    cin>>t>>f>>p;
    for(int i=1;i<=f;i++)
        for(int j=1;j<=f;j++)
            if(i==j)    a[i][j]=0;
            else    a[i][j]=9999999;
    int xx,yy,vv;
    for(int i=1;i<=p;i++)
    {
        cin>>xx>>yy>>vv;
        if(xx!=yy)
          if(a[xx][yy]>vv)    
             { a[xx][yy]=vv;     a[yy][xx]=vv;}
    }
    for(int i=1;i<=f;i++)
    {    dis[i]=a[1][i];
        book[i]=0;
    }
    book[1]=1;
    for(int i=1;i<f;i++)
    {
        int u=1;
        int min=9999999;
        for(int j=1;j<=f;j++)
            if(min>dis[j] && book[j]==0)
            {
                min=dis[j];
                u=j;
            }
        book[u]=1;
        for(int v=1;v<=f;v++)
            if(a[u][v]<9999999)
                if(dis[v]>dis[u]+a[u][v])
                    dis[v]=dis[u]+a[u][v];
    }
    for(int i=1;i<=f;i++)
        if(dis[i]<=t)    ans++;
    cout<<ans<<endl;
    return 0;
}

BELLMAN-FORD

这个主要是判断负环

#include<iostream>
using namespace std;
int n,m;
int a[10010][10010],dis[10010];
int x[10010],y[10010],v[10010];
int main()
{
    cin>>n>>m;
    int xx,yy,vv;
    for(int i=1;i<=m;i++)
        cin>>x[i]>>y[i]>>v[i];
    for(int i=1;i<=n;i++)
        dis[i]=0x7fffffff;
    dis[1]=0;
    for(int k=1;k<n;k++)
        for(int i=1;i<=m;i++)
            if(dis[y[i]]>dis[x[i]]+v[i])
                dis[y[i]]=dis[x[i]]+v[i];
    for(int i=1;i<=n;i++)
        cout<<dis[i]<<endl;
    return 0;
}

SPFA

就是bellman-ford 的队列 用邻接表

/*
by kaike
11/16/2016
*/
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN=10010;
int que[MAXN],dis[MAXN],bok[MAXN],Link[MAXN],len=0,head=0,tail=1;
int m,n,x,y,v;
struct qaq
{
    int next,y,v;
}e[MAXN];
void insert(int xx,int yy,int vv)
{
    e[++len].next=Link[xx];
    Link[xx]=len;
    e[len].y=yy;
    e[lrn].v=vv;
}
void init()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {    cin>>x>>y>>v;
        insert(x,y,v);
        insert(y,x,v);
    }
}
void spfa()
{
    dis[S]=0;
    bok[S]=1;
    que[1]=S;
    head=0; tail=1;
    while(head<tail)
    {
        int t=q[++head];
        bok[t]=0;
        for(int i=Link[t];i;i=e[i].next)
        {
            if(dis[e[i].y]>dis[t]+e[i].v)
            {
                dis[e[i].y]=dis[t]+e[i].v;
                if(bok[e[i].y]==0)
                {
                    que[++tail]=e[i].y;
                    bok[e[i].y]=1;
                }
            }
        }
    }
}
int main()
{
    init();
    spfa();
    return 0;
}

具体看1216.虫洞

1216.虫洞

传送门

就是输入两组数据，一组双向，一组单项负环，用spfa 如果有负环，就说明可以，没有就不可以

#include<iostream>
#include<cstring>
using namespace std;
int f,n,m,w;
int len=0;
int link[510],dis[510];
bool flag,book[510];
struct data
{
    int y,v,next;
}e[100100];
void ins(int xx,int yy,int vv)
{
    e[++len].next=link[xx];
    link[xx]=len;
    e[len].y=yy;
    e[len].v=vv;
}
void spfa(int x)
{
    book[x]=1;
    for(int i=link[x];i;i=e[i].next)
    {
        if(e[i].v+dis[x]<dis[e[i].y])
        {    if(book[e[i].y])    {
                flag=1;
                return ;
            }
            else
            {
                dis[e[i].y]=e[i].v+dis[x];
                spfa(e[i].y);
            }
        }
    }
    book[x]=0;
}
bool judge()
{
    for(int i=1;i<=n;i++)
        dis[i]=book[i]=0;
    flag=0;
    for(int i=1;i<=n;i++)
    {
        spfa(i);
        if(flag)    return 1;
    }
    return 0;
}
int main()
{
    cin>>f;
    while(f--)
    {
        len=0;
        memset(link,0,sizeof(link));
        cin>>n>>m>>w;
        int xx,yy,vv;
        for(int i=1;i<=m;i++)
        {   
            cin>>xx>>yy>>vv;
            ins(xx,yy,vv);
            ins(yy,xx,vv);
        }
        for(int i=1;i<=w;i++)
        {
            cin>>xx>>yy>>vv;
            ins(xx,yy,-vv);
        }
        if(judge()) cout<<"YES"<<endl;
        else    cout<<"NO"<<endl;
    }
    return 0;
}

 如果进队次数>n 就说明有负环。可以用队列，反而dfs不知道怎么写。

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
const int inf=0x7fffffff;
const int N=500+10;
const int M=100100;
int T,n,m,w,xx,yy,vv;
int Link[N],len=0,bok[N],dis[N],upp[N],que[M];
struct student
{
    int y,v,next;
}e[M];
void insert(int xx,int yy,int vv)
{
    e[++len].next=Link[xx];
    Link[xx]=len;
    e[len].y=yy;
    e[len].v=vv;
}
void init()
{
    memset(e,0,sizeof(e));
    memset(Link,0,sizeof(Link));
    len=0;
    scanf("%d %d %d",&n,&m,&w);
    while(m--)
    {
        scanf("%d %d %d",&xx,&yy,&vv);
        insert(xx,yy,vv);
        insert(yy,xx,vv);
    }
    while(w--)
    {
        scanf("%d %d %d",&xx,&yy,&vv);
        insert(xx,yy,-vv);
    }
}
void print()
{
    for(int i=1;i<=n;i++)
        printf("%d ",dis[i]);
    printf("
");
}
int spfa()
{
    memset(upp,0,sizeof(upp));
    memset(bok,0,sizeof(bok));
    memset(que,0,sizeof(que));
    for(int i=1;i<=n;i++)
        dis[i]=inf;
    int head=1,tail=2;
    dis[1]=0;
    que[1]=1;
    bok[1]=1;
    while(head<tail)
    {
        int tt=que[head];
        bok[tt]=0;
        for(int i=Link[tt];i;i=e[i].next)
        {
            if(dis[e[i].y]>dis[tt]+e[i].v)
            {
                dis[e[i].y]=dis[tt]+e[i].v;
                if(bok[e[i].y]==0)
                {
                    que[tail++]=e[i].y;
                    bok[e[i].y]=1;
                    upp[e[i].y]++;
                }
                if(upp[e[i].y]>n)
                        return 0;
            }
        }
        head++;
    }
    return 1;
}
int main()
{
    scanf("%d",&T);
    while(T--)
    {
    init();
    if(spfa())
        printf("NO
");
    else printf("YES
");
    }
    return 0;
}

（超时code）

1215.香甜的黄油

传送门

构建一个双向图

然后spfa 好像是第一个超时是因为没有 book 数组标记

然后记录所有需要的最小值

#include<iostream>
#include<cstring>
using namespace std;
int n,p,c;
int a[850][850],b[510],dis[850],q[100100];
int maxx=99999999,sum;
void spfa(int x)
{
    memset(dis,260,sizeof(dis));
    int head=0,tail=1;
    q[0]=x;
    dis[x]=0;
    while(head<tail)
    {
        for(int i=1;i<=p;i++)
            if(dis[i]>a[q[head]][i]+dis[q[head]])
            {
                q[tail++]=i;
                dis[i]=a[q[head]][i]+dis[q[head]];
            }
        head++;
    }
    sum=0;
    for(int i=1;i<=n;i++)
        sum+=dis[b[i]];
}
int main()
{
    memset(a,260,sizeof(a));
    cin>>n>>p>>c;
    for(int i=1;i<=n;i++)
        cin>>b[i];
    int xx,yy,vv;
    for(int i=1;i<=c;i++)
    {
        cin>>xx>>yy>>vv;
        a[xx][yy]=a[yy][xx]=vv;
    }
    for(int i=1;i<=p;i++)
    {
        spfa(i);
        if(maxx>sum)    maxx=sum;
    }
    cout<<maxx<<endl;
    return 0;
}

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int n,p,c;
bool book[1010];
int len=0,ans=0x7fffffff;
int b[850],q[100010],dis[1000],link[1000];
struct ha
{
    int y,next,v;
}e[15000];
void insert(int xx,int yy,int vv)
{
    e[++len].next=link[xx];
    link[xx]=len;
    e[len].y=yy;
    e[len].v=vv;
}
int spfa(int x)
{
    memset(dis,10,sizeof(dis));
    memset(book,0,sizeof(book));
    dis[x]=0;   
    book[x]=1;
    q[1]=x;
    int head=0,tail=1,sum=0;
    while(head<tail)
    {
        int tn=q[++head];
        book[tn]=0;
        int te=link[tn];
        for(int i=te;i;i=e[i].next)
        {
            int tmp=e[i].y;
            if(dis[tmp]>dis[tn]+e[i].v)
            {
                dis[tmp]=dis[tn]+e[i].v;
                if(!book[tmp])
                {
                    book[tmp]=1;
                    q[++tail]=tmp;
                }
            }
        }
    }
    for(int i=1;i<=n;i++)
        sum+=dis[b[i]];
    return sum;
}
int main()
{
    cin>>n>>p>>c;
    for(int i=1;i<=n;i++)
        cin>>b[i];
    int xx,yy,vv;
    for(int i=1;i<=c;i++)
    {
        cin>>xx>>yy>>vv;
        insert(xx,yy,vv);
        insert(yy,xx,vv);
    }
    for(int i=1;i<=p;i++)
        ans=min(spfa(i),ans);
    cout<<ans<<endl;
    return 0;
}

易错点阿喂

1.邻接矩阵必须判断重边（看要最大值还是最小值）

2.邻接矩阵注意范围（5000以上就会爆）

不过可以用邻接表对拍

3.link是关键字，这个坏习惯要改掉！！

4.注意e数组的范围，无向图 e*2，有向图e 

---------------------分割线----------------------------

最小生成树。

prim

void prim(int S)
{
    memset(dis,10,sizeof(dis));
    memset(bok,0,sizeof(bok));
    bok[S]=1;
    for(int i=1;i<=n;i++)
        dis[i]=a[S][i];
    summ=0;
    for(int i=1;i<n;i++)
    {
        int minn=a[0][0],c=0;
        for(int j=1;j<=n;j++)
            if(minn>dis[j]&&bok[j]==0)
            {
                minn=dis[j];
                c=j;
            }
        bok[c]=1;
        summ+=minn;
        for(int j=1;j<=n;j++)
            if(dis[j]>a[c][j]&&bok[j]==0)
                dis[j]=a[c][j];
    }
}

kruskal

/*
by kaike
11/16/2016
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<cstdio>
using namespace std;
int kk=0,sum=0;
int getf(int v)
{
    if(f[v]!=v)
        f[v]=getf(f[v]);
    return f[v];
}
int merge(int v,int u)
{
    int t1=getf(v),t2=getf(u);
    if(t1!=t2)
    {    f[t2]=t1;
        return 1;
    }
    return 0;
}
void kruskal()
{
    for(int i=1;i<=n;i++)
    {
        if(meige(e[i].next,e[i].y))
        {
            kk++;
            sum+=e[i].v;
        }
        if(kk==n-1) break;
    }
}
int main()
{
    kruskal();
    cout<<sum<<endl;
    return 0;
}

 割点

/*
by kaike
11/16/2016
*/
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<string>
using namespace std;
const int MAXN=5010;
int n,e[MAXN][MAXN];
int num[MAXN],low[MAXN],bok[MAXN];
int root=1,ans=0,x,y,index=0;
void init()
{
    cin>>n;
    while(cin>>x>>y)
    {
        e[x][y]=1;
        e[y][x]=1;
    }
}
void dfnlow(int cur,int father)
{
    int child=0;
    index++;
    num[cur]=index;
    low[cur]=index;
    for(int i=1;i<=n;i++)
        if(e[cur][i]==1)
        {
            if(num[i]==0)
            {
                child++;
                dfnlow(i,cur);
                low[cur]=min(low[cur],low[i]);
                if(cur!=root&& low[i]>=num[cur])
                    bok[cur]=1;
                if(cur==root && child==2)
                    bok[cur]=1;
            }
            else if(i!=father)
                low[cur]=min(low[cur],num[i]);
        }
}
int main()
{
    init();    
    dfnlow(1,root);
    for(int i=1;i<=n;i++)
        if(bok[i]==1)   ans++;
    cout<<ans<<endl;
    for(int i=1;i<=n;i++)
        if(bok[i]==1)  cout<<i<<endl;
    return 0;
}

割边

/*
by kaike
11/16/2016
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<cstdio>
using namespace std;
const int MAXN=5010;
int n,m,e[160][160],x,y,len=0;
int num[MAXN],low[MAXN],index=0,bok[MAXN],root=1;
struct qaq
{
    int aa,bb;
}a[MAXN];
bool cmp(qaq x,qaq y)
{
    return (x.aa<y.aa ||(x.aa==y.aa && x.bb<y.bb ));
}
void init()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>x>>y;
        e[x][y]=1;
        e[y][x]=1;
    }
}
void dfnlow(int cur,int father)
{
    int child=0;
    index++;
    num[cur]=index;
    low[cur]=index;
    for(int i=1;i<=n;i++)
        if(e[cur][i]==1)
        {
            if(num[i]==0)
            {
                child++;
                dfnlow(i,cur);
                low[cur]=min(low[cur],low[i]);
                if(low[i]>num[cur])
                {   a[++len].aa=cur;
                    a[len].bb=i;
                }
            }
            else if(i!=father)
                low[cur]=min(low[cur],num[i]);
        }
}
int main()
{
    init();
    dfnlow(1,root);
    sort(a+1,a+len+1,cmp);
    for(int i=1;i<=len;i++)
        cout<<a[i].aa<<' '<<a[i].bb<<endl;
    return 0;
}

有向图的强联通分量

无向图的边双联通分量

这样看来好像图也没有很难

不懂为什么学东西的时候遇到题目都不会

归根结底还是知识点不熟悉

感觉这样一总结都清晰了好多

嗯

不言谢

只赴汤蹈火