今天(2021-11-01)晚上看到 数学吧 的 一题 《实在想不出来了》 https://tieba.baidu.com/p/7596415471

大概知道怎么做了, 但是 lim xn , n -> 无穷 的 地方 还要想一下, 题目 似乎 有点问题, 应该要求 f (x) 在 [ 0, 1 ] 上 要么 大于 1, 要么 小于 1 , 如果 f (x) 在 [ 0, 1 ] 上 有 小于 1 也有 大于 1, 那 lim xn , n -> 无穷 似乎不存在,就是说 n -> 无穷 时, xn 并不收敛, 而是 受 无穷 支配 而 不能确定 值 。
@思维机器 可以看看
@已封12138
本文已发到了 反相吧 《数学吧 的 一题 《实在想不出来了》》 https://tieba.baidu.com/p/7597152622 。
2 楼
思维机器 : 收到
3 楼
思维机器 : 用中值定理证明
K歌之王: 我在 《实在想不出来了》 的 回复 里 看到 好几次 “积分中值定理”, 以前也看到过, 但 我 不知道 积分中值定理 是 什么 , 我在下面 发 我的 做法 。
思维机器: 回复 K歌之王 :积分中值定理有个公式,大概意思就是函数区间的积分等于区间某点的函数值乘以区间长度,这很直观的。还有微分形式的,就是拉格朗日中值定理
K歌之王 :回复 散步的鱼 :这么一说 就 明白了, 这个 积分中值 类似 交流电 的 有效值,在 物理 里 应该会 经常 见到 等效均值点 的 场景 。 刚也看了一下 拉格朗日中值定理 。
散步的鱼: 回复 K歌之王 :最近忙啊,没精力深搞
4 楼
K歌之王 :
因为 f ( x ) 在 [ 0, 1 ] 非负单增, 所以, [ f ( x ) ]^n 在 [ 0, 1 ] 上 的 定积分 就可以 妥妥的 表示 为 [ f ( x ) ]^n 和 x 轴 在 [ 0, 1 ] 上 围成的 曲边形面积 。
将 [ f ( x ) ]^n 在 [ 0, x ] 上 的 定积分 记为 F ( x ), 可知 F ( 0 ) = 0 , 当 0 < x <= 1 时, F ( x ) > 0 , F ( x ) 在 [ 0, 1 ] 上 也是 单增 的 。
要 证明 题目(存在 唯一 的 xn), 只要 证明 [ f ( 0 ) ]^n <= F ( 1 ) <= [ f ( 1 ) ]^n ,
要 怎么 证明 [ f ( 0 ) ]^n <= F ( 1 ) <= [ f ( 1 ) ]^n ?
比如, 直线 y = [ f ( 1 ) ]^n , 直线 x = 1 和 x 轴 y 轴 围成的 长方形面积 是 大于 F ( 1 ) 的 , 然后 …… 嘿嘿
5 楼
K歌之王 :
回复 3 楼 @思维机器 “最近忙啊,没精力深搞” ,
大家加油, 哈哈 。
微分形式 的 中值定理, 也就是 拉格朗日中值定理 和 泰勒级数 颇有渊源, 或者说,泰勒级数 受到 中值定理 的 影响 和 思想上 的 启发 。
把 f ( x ) 在 [ a,b ] 上 的 增量 等价 为 一条 斜率 为 k 的 直线 在 [ a, b ] 上 的 增量, 以此 列一个 方程, 用 微分方程 的 方法 来 解 这个 方程, 得到的就是 泰勒级数 。
这几天看知乎看到, 伽罗华 和 阿贝尔 解决 一元五次以上方程 没有 代数解 的 问题 前, 拉格朗日 (还是 拉普拉斯 ? 分不清 这两位) 就 觉得 五次以上方程 的 根 可能 不能用 根式 表达 。
而 傅里叶级数 出现 前, 数学家们 (拉格朗日 ? 拉普拉斯 ?) 也 隐约觉得 周期函数 可以 表示 为 正弦级数 。 而 傅里叶 凭 直觉 就 说 周期函数 可以 表示 为 正弦级数 。
看来 大师 们 的 杰作 也是 在 之前 的 大师 和 之前的之前的 大师的大师 那里 受到 启示 积累 一点一点 发展 来 的 。
6 楼
K歌之王 :
5 楼 说到的 知乎 《能说说你们心目中的数学大咖(数学家or教授都行),并且能介绍几个有关他(她)们与数学的故事吗?》 https://www.zhihu.com/question/372642069/answer/1022511118




一开始 想的 比较简单, f ( x ) 在 [ 0, 1 ] 上 非负连续严格增, 所以, [ f ( x ) ] ^ n 也是 非负连续严格增, 若 f ( x ) > 1, 当 n -> 无穷 时, [ f ( x ) ] ^ n 的 增幅猛烈, 直插云霄 。
但 当时 不知怎的, 考虑的 时候 一直 把 f ( 0 ) 认为 是 0, 即 f ( 0 ) = 0, 当然 题目条件 是 f ( x ) 在 [ 0, 1 ] 上 非负, 也就是 f ( 0 ) > 0 , 但, 把 f ( 0 ) 认为 是 0 , 即 f ( 0 ) = 0 可以 更加 发现 无穷 和 极限 的 有趣现象, 所以 我们 接下来 的 讨论 中 仍然认为 f ( 0 ) = 0 。
设 f ( x ) 和 n 无关, 也就是 f ( x ) 里 没有 n 。
若 x ∈ ( 0, 1 ] , f ( x ) < 1 , 当 n -> 无穷 时, [ f ( x ) ] ^ n -> 0 , 那么 [ f ( x ) ] ^ n 在 [ 0, 1 ] 上的 定积分 ʃ [ f ( x ) ] ^ n dx , [ 0, 1 ] 也 趋于 0 , 此时, ( 0, 1 ] 上 的 任意一个 x 都能满足 f ( x ) -> 0 , 也就是 ( 0, 1 ] 上 的 任意一个 x 都可以作为 xn, 其实 x = 0 也可以, f ( 0 ) = 0 , 和 f ( 0 ) -> 0 也差不多 吧 ? 那 算上 x = 0, [ 0, 1 ] 上的 任意 一个 x 都 可以 作为 xn , 但 这 好像 和 题意 “唯一的 xn” 不一致 了 ?
这些 是 刚开始 做 这题 时 的 想法, 后来没过几天, 在 做 《又 看到 数学吧 的 两题》 https://www.cnblogs.com/KSongKing/p/15522312.html 里 的 题 的 时候 发现, 一个 函数 f ( x ) , 在 [ 0, 1 ) 上 处处 无穷小, 但是 它 在 [ 0, 1 ] 上 的 定积分 不一定 是 无穷小, 也可能是 常数 或 无穷, 这 和 f ( 1 ) 的 值 有关 。
当然, 我们 这里 的 f ( 0 ) = 0 , 在 x ∈ ( 0, 1 ] , f ( x ) < 1 , 也就是 f ( 1 ) < 1, 当 n -> 无穷 时, [ f ( 1 ) ] ^ n -> 0 , 所以 f ( x ) 在 [ 0, 1 ] 上 的 定积分 是 无穷小 还是 成立 的 。
若 x ∈ ( 0, 1 ] , f ( x ) = 1 , 当然, 这种情况 是 不存在的, 因为 f ( x ) 非负连续严格增 。
若 x ∈ ( 0, 1 ] , f ( x ) > 1 , 当 n -> 无穷 时, [ f ( x ) ] ^ n -> 无穷 , 但 f ( 0 ) = 0 。
因为 [ 0, 1 ] 在 x 轴 上 的 长度 为 1, 所以, 要让 [ f ( xn ) ] ^ n = ʃ [ f ( x ) ] ^ n dx , [ 0, 1 ] , 只要让 直线 y = f ( xn ) 在 [ 0, 1 ] 里 和 x 轴 围成 的 长方形面积 等于 [ f ( x ) ] ^ n 在 [ 0, 1 ] 里 和 x 轴 围成 的 曲边形面积 就行了 。
那么 这个 曲边形 的 面积 是 多大 ? 首先看一下 这个 曲边形 的 形状 。
一开始 想的 比较简单, f ( x ) 在 [ 0, 1 ] 上 非负连续严格增, 所以, [ f ( x ) ] ^ n 也是 非负连续严格增, 若 f ( x ) > 1, 当 n -> 无穷 时, [ f ( x ) ] ^ n 的 增幅猛烈, 直插云霄 。
既然 除了 x = 0 外, 从 x > 0 开始, 每个 x 的 [ f ( x ) ] ^ n 都 无穷大, 直插云霄, 一个 比一个 飞的 更高, 高到看不见, 那 这些 一个比 一个高, 高 到 没影 的 [ f ( x ) ] ^ n 连起来 的 曲线 也是 一条 直插云霄 的 “冲天线” 吧 ? 大概 这个样子 :
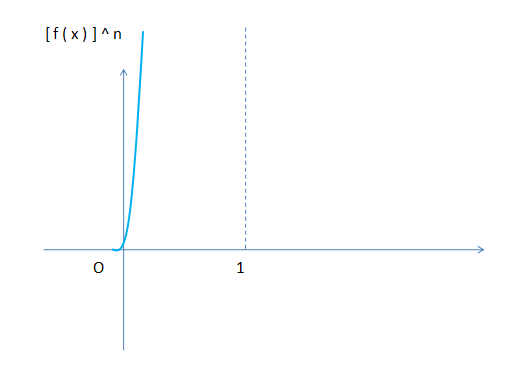
[ f ( x ) ] ^ n 曲线 无限趋于 和 x 轴 垂直, 和 y 轴 平行, 无限趋于 直线, 所以, 它 和 x 轴 在 [ 0,1 ] 上 围成 曲边形 应该是 无限趋于 一个 向上 无限开口 的 长方形 吧 ?
这 和 直线 x = 1 (图中 虚线) 和 y 轴 、x 轴 在 x ∈ [ 0, 1 ] 上 围成 的 向上 无限开口 的 长方形 差不多 吧 ?
两个 长方形 无限趋于 重合, 当然 两者 的 面积 无限趋于 相同 。
两个 长方形 的 宽 都是 1,
直线 x = 1 的 高度 是 无穷, y = 无穷, 长方形 面积 = 无穷 * 1 = 无穷
所以, [ f ( x ) ] ^ n 曲线 和 x 轴 在 [ 0,1 ] 上 围成 曲边形 无限趋于 长方形, 长方形 的 高 应该是 最大 的 那个 [ f ( x ) ] ^ n, 即 [ f ( 1 ) ] ^ n , 当然 [ f ( x ) ] ^ n 也是 无穷 , 于是 ʃ [ f ( x ) ] ^ n dx , [ 0, 1 ] = [ f ( x ) ] ^ n 曲边形面积 = 长方形面积 = [ f ( 1 ) ] ^ n * 1 = [ f ( 1 ) ] ^ n ,
即 ʃ [ f ( x ) ] ^ n dx , [ 0, 1 ] = [ f ( 1 ) ] ^ n
我们 要找的 xn 要 满足 [ f ( xn ) ] ^ n = ʃ [ f ( x ) ] ^ n dx , [ 0, 1 ] , 由 上式 , 显然, xn = 1 , 因为 曲边形 趋于 长方形 , 所以也可以说 xn -> 1 。
因为 曲边形 无限趋于 长方形, 因此, f ( x ) 还可以 画成 这样子 :

但 [ f ( x ) ] ^ n 曲线 不是 无限 趋于 竖直 的 直线 吗 ? (竖直 指 垂直于 x 轴) 那 个 “横过来” 的“ 封顶” 是 怎么回事 ? 好吧, 我们可以这样说服自己, [ f ( x ) ] ^ n 曲线 只有 上升 到 “最高” 的 时候 才 “甩过来” 封顶, 最高 是 多高 ? 是 [ f ( 1 ) ] ^ n ? 是 无穷 ? 是 永远到达 不了 ?
这是 只看 f ( x ) 的 定义域 是 [ 0, 1 ] ,
如果 f ( x ) 的 定义域 是 x 轴 正半轴, 也是 非负连续严格增, 那 是 在 什么时候 “甩过来” ? 是在 [ f ( 1 ) ] ^ n ? [ f ( 2 ) ] ^ n ? [ f ( 3 ) ] ^ n ? [ f ( 无穷 ) ] ^ n ?
若 在 x ∈ ( 0. 1 ] 上, 有 f ( x ) < 1, 也有 f ( x ) > 1, 就有一些问题了 。 设 f ( 0.4 ) = 1, 因为 f ( x ) 连续严格增, 当然, 在 x ∈ ( 0. 0.4 ) , f ( x ) < 1, 在 x ∈ ( 0.4. 1 ] , f ( x ) > 1 。
