题目链接：https://www.lydsy.com/JudgeOnline/problem.php?id=4815
题意概述：要认真概述的话这个题就出来了。。。
分析：
首先分析题目，认真研究一下修改操作，想到一个问题：满足什么样的条件的格子会互相影响？
看到式子，一想，这正是辗转相除？迅速意识到行列的gcd相同的格子会互相影响。
然后我们再利用一下系数的关系，把式子变成f(a,a+b)/(a+b)=f(a,b)/b，发现当行相同的时候格子之间的值与所处列数成正比关系，因为题目保证了f(a,b)=f(b,a)，同样的性质也会出现在列相同的情况下。对于任意两个互相影响的格子，都可以先变换行坐标再变换列坐标互相到达，于是有：f(a,b)/(a*b)=f(x,y)/(x*y)。
然后你发现有了这个性质，我们就可以用一维空间来储存所有的格子的值了~
令gcd(i,j)=g，那么f(i,j)=f(g,g)*(i*j)/(g*g)。我们令f(g)=f(g,g)，所有格子(i,j)的值都可以由f(gcd(i,j))得到。
所以有：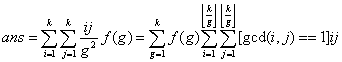
我们令：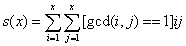
，则
考虑一下s(x)的计算，我们枚举i，然后枚举所有小于i的j，如果i,j互质，我们就统计进入答案，可以看成是统计所有小于i且与i互质的j的和乘以i统计进入答案，根据对称性，另一半方阵是一样的，单独处理对角线上的唯一有贡献的(1,1)即可。
有一个神奇的公式：小于i且和i互质的正整数的和为phi(i)*i/2（证明：对于一个小于i的x，gcd(i,x)=1，有gcd(i,i-x)=1，也就是说小于i且与i互质的数是成对出现的，并且每一对的和为i，一共有phi(i)/2对）。（对s(x)的计算也可以莫比乌斯反演，借助[gcd(i,j)==1]=[sum{ mu(k) | k|i,k|j,即k|gcd(i,j) }==1]，但是我只探索出了70分的世界线......）
所以：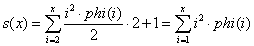
，可以直接预处理出来。
最后我们只要用一个分块支持O(sqrt(n))修改，O(1)查询，加上用O(sqrt(k))枚举k的约数就可以做到每组询问O(sqrt(n)+sqrt(k))的时间回答了（有的时候分块的O(1)询问是个很棒的东西，弄个树状数组就自寻烦恼了，分块有点小细节，一定要把f(x)的值原原本本地存起来，不能取模）。
时间复杂度O(M(sqrt(N)+sqrt(K)))。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<algorithm> 6 #include<cmath> 7 #include<queue> 8 #include<set> 9 #include<map> 10 #include<vector> 11 #include<cctype> 12 using namespace std; 13 const int MAXN=4000005; 14 const int mo=1000000007; 15 typedef long long LL; 16 17 int M,N,K; 18 int pri[MAXN],tot,phi[MAXN],s[MAXN]; 19 bool ntp[MAXN]; 20 struct Block{ 21 static const int maxn=4000005; 22 static const int size=2999; 23 static const int maxm=2010; 24 int sum[maxn],flag[maxm],L[maxm],R[maxm],cnt,sz,belong[maxn]; 25 LL f[maxn]; 26 Block(){ sz=0; } 27 void build(int n){ 28 for(sz=1;sz+size<n;sz+=size){ 29 cnt++,L[cnt]=sz,R[cnt]=sz+size; 30 for(int j=L[cnt];j<R[cnt];j++) 31 f[j]=1ll*j*j,sum[j]=(sum[j-1]+f[j]%mo)%mo,belong[j]=cnt; 32 flag[cnt]=0; 33 } 34 cnt++,L[cnt]=sz,R[cnt]=n+1; 35 for(int j=L[cnt];j<R[cnt];j++) 36 f[j]=1ll*j*j,sum[j]=(sum[j-1]+f[j]%mo)%mo,belong[j]=cnt; 37 flag[cnt]=0; 38 sz=n; 39 } 40 void update(int p,LL v){ 41 int delt=((v-f[p])%mo+mo)%mo; 42 f[p]=v; 43 for(int i=p;i<R[belong[p]];i++) 44 sum[i]=(sum[i]+delt)%mo; 45 for(int i=belong[p]+1;i<=cnt;i++) 46 flag[i]=(flag[i]+delt)%mo; 47 } 48 int query(int p){ 49 return (sum[p]+flag[belong[p]])%mo; 50 } 51 }block; 52 53 void ready() 54 { 55 ntp[0]=ntp[1]=1,phi[1]=1; 56 for(int i=2;i<=N;i++){ 57 if(!ntp[i]) pri[++tot]=i,phi[i]=i-1; 58 for(int j=1;j<=tot&&1ll*pri[j]*i<=N;j++){ 59 ntp[pri[j]*i]=1; 60 if(i%pri[j]==0){ 61 phi[i*pri[j]]=phi[i]*pri[j]; 62 break; 63 } 64 phi[i*pri[j]]=phi[i]*(pri[j]-1); 65 } 66 } 67 block.build(N); 68 for(int i=1;i<=N;i++) 69 s[i]=(s[i-1]+1ll*i*i%mo*phi[i]%mo)%mo; 70 } 71 int gcd(int x,int y){ return !y?x:gcd(y,x%y); } 72 void work() 73 { 74 scanf("%d%d",&M,&N); 75 ready(); 76 int a,b,k,p,ans,d; LL x; 77 for(int i=1;i<=M;i++){ 78 scanf("%d%d%lld%d",&a,&b,&x,&k); 79 p=gcd(a,b); 80 block.update(p,x/(a/p)/(b/p)); 81 ans=0; 82 for(int g=1,last;g<=k;g=last+1){ 83 last=k/(k/g); 84 d=((block.query(last)-block.query(g-1))%mo+mo)%mo; 85 ans=(ans+1ll*s[k/g]*d%mo)%mo; 86 } 87 printf("%d ",ans); 88 } 89 } 90 int main() 91 { 92 work(); 93 return 0; 94 }