完全二叉树
叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。如下图
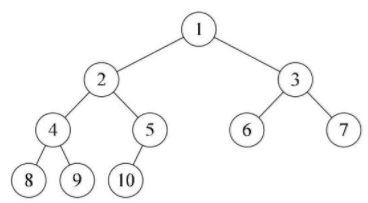
满二叉树
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点二叉树。
国内教程定义:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
国外(国际)定义:a binary tree T is full if each node is either a leaf or possesses exactly two childnodes.大意为:如果一棵二叉树的结点要么是叶子结点,要么它有两个孩子结点,这样的树就是满二叉树。
国内定义的满二叉树:
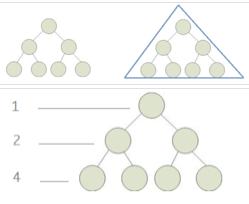
从图形形态上看,满二叉树外观上是一个三角形。从数学上看,满二叉树的各个层的结点数形成一个首项为1,公比为2的等比数列。因此由等比数列的公式,满二叉树满足如下性质:
1、一个层数为k 的满二叉树总结点数为: 。因此满二叉树的结点树一定是奇数个。
。因此满二叉树的结点树一定是奇数个。
2、第i层上的结点数为:
3、一个层数为k的满二叉树的叶子结点个数(也就是最后一层):
完全二叉树的特点是:
1)只允许最后一层有空缺结点且空缺在右边,即叶子结点只能在层次最大的两层上出现;
2)对任一结点,如果其右子树的深度为j,则其左子树的深度必为j或j+1。 即度为1的点只有1个或0个
对于国外的满二叉树
满二叉树的结点要么是叶子结点,度为0,要么是度为2的结点,不存在度为1的结点。
因此,右图中这个二叉树也是满二叉树。但是按照国内的定义,它却不是满二叉树。
声明:大部分内容摘抄自百度百科
