对于数组,查找速度快,而添加和删除速度慢;链表,查找速度慢,而添加和删除速度快;树具备查找、增删速度快的特点
树的常用术语
- 路径:从一个节点到另一个节点,所经过的节点的顺序排列称为'路径’
- 根:树顶端的节点称为根。一棵树只有一个根,如果要把一个节点和边的集合称为树,那么从根到其他任何一个节点都必须有且只有一条路径
- 父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点
- 子节点:一个节点含有的子树的根节点称为该节点的子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点
- 叶节点:没有子节点的节点称为叶节点,也叫叶子节点
- 子树:每个节点都可以作为子树的根,它和它所有的子节点、子节点的子节点等都包含在子树中
- 节点的层次:从根开始定义,根为第一层,根的子节点为第二层,以此类推
- 深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0
- 高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0
二叉树
树的每个节点最多只能有两个子节点
二叉搜索树
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树
二叉树的节点类
public class Node {
private int data;//节点保存数据
private Node leftChild;//左节点
private Node rightChild;//右节点
public Node(int data) {
this.data = data;
}
public void display(){
System.out.println(data);
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public Node getLeftChild() {
return leftChild;
}
public void setLeftChild(Node leftChild) {
this.leftChild = leftChild;
}
public Node getRightChild() {
return rightChild;
}
public void setRightChild(Node rightChild) {
this.rightChild = rightChild;
}
}
二叉树方法
public interface Tree {
/**
* 查找节点
* @param data
* @return
*/
Node find(int data);
/**
* 插入节点
* @param data
* @return
*/
boolean insert(int data);
/**
* 删除节点
* @param key
* @return
*/
boolean delete(int key);
/**
* 中序遍历 左子树-》根节点-》右子树
* @param current
*/
void inOrder(Node current);
/**
* 前序遍历:根节点-》左子树-》右子树
* @param current
*/
void preOrder(Node current);
/**
* 后序遍历:左子树-》右子树-》根节点
* @param current
*/
void postOrder(Node current);
/**
* 查找最大值节点
* @return
*/
Node findMax();
/**
* 查找最小值节点
* @return
*/
Node findMin();
}
二叉搜索树实现
查找方法
查找时候,从根节点开始遍历
- 需要查找的值比当前节点值大,搜索右子树
- 需要查找的值等于当前节点的值,停止搜索,返回当前节点
- 需要查找的值比当前节点值小,搜索左子树
public Node find(int key) {
Node current = root;
if (current == null) return null;
while (current != null){
if (current.getData()>key){
current = current.getLeftChild();
}else if (current.getData() < key){
current = current.getRightChild();
}else return current;
}
return null;
}
插入方法
插入值时候,先确定需要插入的位置。先与根节点比较,如果值大于根节点的值,则与右子树比较,反之亦然
public boolean insert(int data) {
Node newNode = new Node(data);
if (root == null){
root = newNode;
return true;
}else {
Node current = root;
Node parentNode = null;
while (current != null){
parentNode = current;
if (current.getData() > data){//如果插入值小于当前节点的值
current = current.getLeftChild();//获取当前节点的左节点
if (current == null){//如果为空,当前值插入该位置
parentNode.setLeftChild(newNode);
return true;
}
}else {
current = current.getRightChild();
if (current == null){
parentNode.setRightChild(newNode);
return true;
}
}
}
}
return false;
}
遍历方法
遍历树是按照一定的顺序访问树的每一个节点
- 中序遍历:左子树-》根节点-》右子树
- 前序遍历:根节点-》左子树-》右子树
- 后序遍历:左子树-》右子树-》根节点
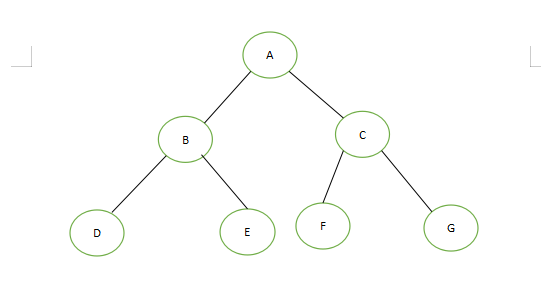
中序遍历:DBEAFCG
前序遍历:ABDECFG
后序遍历:DEBFGCA
@Override
public void inOrder(Node current) {
if (current != null){
inOrder(current.getLeftChild());
System.out.print(current.getData());
inOrder(current.getRightChild());
}
}
@Override
public void preOrder(Node current) {
if (current!= null){
System.out.print(current.getData());
preOrder(current.getLeftChild());
preOrder(current.getRightChild());
}
}
@Override
public void postOrder(Node current) {
if (current!= null){
postOrder(current.getLeftChild());
postOrder(current.getRightChild());
System.out.print(current.getData());
}
}
查找最大最小值方法
最大最小值,就是一直查询右/左节点直到右/左节点不存在,就是最大/小值
@Override
public Node findMax() {
Node current = root;
Node maxNode = root;
while (current != null){
maxNode = current;
current = current.getRightChild();
}
return maxNode;
}
@Override
public Node findMin() {
Node current = root;
Node minNode = root;
while (current != null){
minNode = current;
current = current.getLeftChild();
}
return minNode;
}
删除方法
删除时候分为三种情况
1. 删除节点不包含子节点
2. 删除节点包含一个子节点
3. 删除节点包含两个子节点
- 删除节点不包含子节点
只需改变删除节点的父节点引用该节点的值,将其指向null。要删除的节点不再引用,等待垃圾回收器回收即可
- 删除节点包含一个子节点
删除节点的父节点指向删除节点的子节点
- 删除节点包含两个子节点
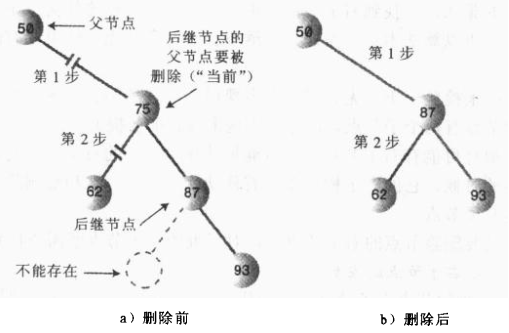
对于删除节点存在两个子节点时候,删除后,两个子节点需要重新构成一个新的子树,删除节点的父节点指向新的子树,
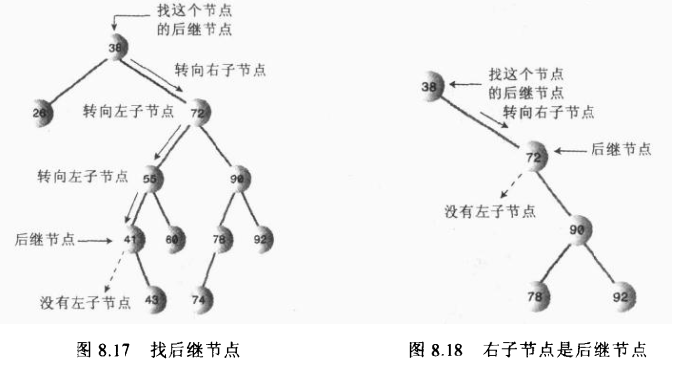
子树的根节点为删除节点的后继节点。后继节点也就是比删除节点大的最小节点
确认后续节点后,又需要考虑后续节点时候是否为删除节点的位置
- 后续节点是删除节点的右子节点
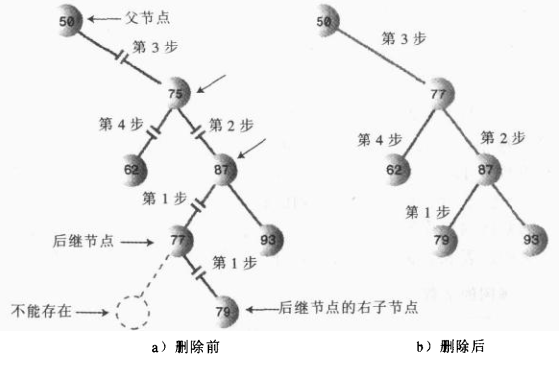
- 后续节点不是删除节点的右子节点,则必定为删除节点的右子节点的左子节点
public boolean delete(int key) {
if (root == null) return false;//树为空,返回false
Node current = root;
Node parent = root;
boolean isLeftChild = false;//用于判断需要删除的节点是其父节点的左/右子节点
while (current.getData() != key){
parent = current;
if (key > current.getData()){
isLeftChild = false;
current = current.getRightChild();
}else {
isLeftChild = true;
current = current.getLeftChild();
}
if (current == null)return false;//未找到,返回false
}
if (current.getRightChild() == null &&
current.getLeftChild() == null){//需要删除的节点不包含子节点
if (current == root){
root = null;
}else if (isLeftChild){
parent.setLeftChild(null);
}else parent.setRightChild(null);
}else if (current.getRightChild() == null &&
current.getLeftChild() != null){//需要删除的节点包含一个节点,且为左节点
if (current == root){
root = current.getLeftChild();
}else if (isLeftChild){
parent.setLeftChild(current.getLeftChild());
}else parent.setRightChild(current.getLeftChild());
}else if (current.getRightChild() != null &&
current.getLeftChild() == null){//需要删除的节点包含一个节点,且为右节点
if (current == root){
root = current.getRightChild();
}else if (isLeftChild){
parent.setLeftChild(current.getRightChild());
}else {
parent.setRightChild(current.getRightChild());
}
}else {//需要删除的节点包含两个节点
Node successor = geSuccessor(current);//获得后继节点
if (current == root){
root = successor;
}else if (isLeftChild){
parent.setLeftChild(successor);
}else parent.setRightChild(successor);
successor.setLeftChild(current.getLeftChild());
}
return true;
}
private Node geSuccessor(Node delNode) {
Node successorParent = delNode;
Node successor = delNode;
Node current = delNode.getRightChild();
while (current != null){
successorParent = successor;
successor = current;
current = current.getLeftChild();
}
if (successor != delNode.getRightChild()){//后继节点不是需要删除节点的右节点,调整结构
successorParent.setLeftChild(successor.getRightChild());
successor.setRightChild(delNode.getRightChild());
}
return successor;
}
完整的二叉查找树代码
https://github.com/Jzedy/Z-books/blob/master/src/main/test/java/treeStart/BinaryTree.java