BZOJ3073 Journeys

题目描述

Seter建造了一个很大的星球，他准备建造N个国家和无数双向道路。N个国家很快建造好了，用1..N编号，但是他发现道路实在太多了，他要一条条建简直是不可能的！于是他以如下方式建造道路：(a,b),(c,d)表示，对于任意两个国家x,y，如果a<=x<=b,c<=y<=d，那么在xy之间建造一条道路。Seter保证一条道路不会修建两次，也保证不会有一个国家与自己之间有道路。
Seter好不容易建好了所有道路，他现在在位于P号的首都。Seter想知道P号国家到任意一个国家最少需要经过几条道路。当然，Seter保证P号国家能到任意一个国家。

注意：可能有重边

输入格式

第一行三个数N,M,P。N<=500000,M<=100000。
后M行，每行4个数A，B，C，D。1<=A<=B<=N,1<=C<=D<=N。

输出格式

N行，第i行表示P号国家到第i个国家最少需要经过几条路。显然第P行应该是0。

样例

样例输入

5 3 4
1 2 4 5
5 5 4 4
1 1 3 3

样例输出

1
1
2
0
1

solutions：

你当然可以暴力，据说会拿不少分

但追求卓越的我们是一定要打正解的

 

我们发现这是对区间里的点建边，我一想就想到了线段树

建图我们用两棵线段树，线段树上的边权都是0：

进树： 从父亲向儿子连边(0)，表示能达到该区间就能达到该区间的子区间。
出树：从儿子向父亲连边(0)，表示能从该区间出发就能从该区间的父区间出发。

我们需要在两树的节点上建边，假如我们对[a,b]和[c,d]上的点连边，那么我们定义两个虚拟节点p1,p2;

线段树中[a,b]和p1连一条边权为0的边，[c,d]和p2连一条边权为0的边，然后将p1和p2用边权为1的点连接起来，就完成了[a,b]和[c,d]上的点连边

例如5个节点中连边[2, 3] <----> [4, 5]（此处就只连单向边示意，且这张图连边时只用了一个虚拟节点，不过对整体没有影响）

 

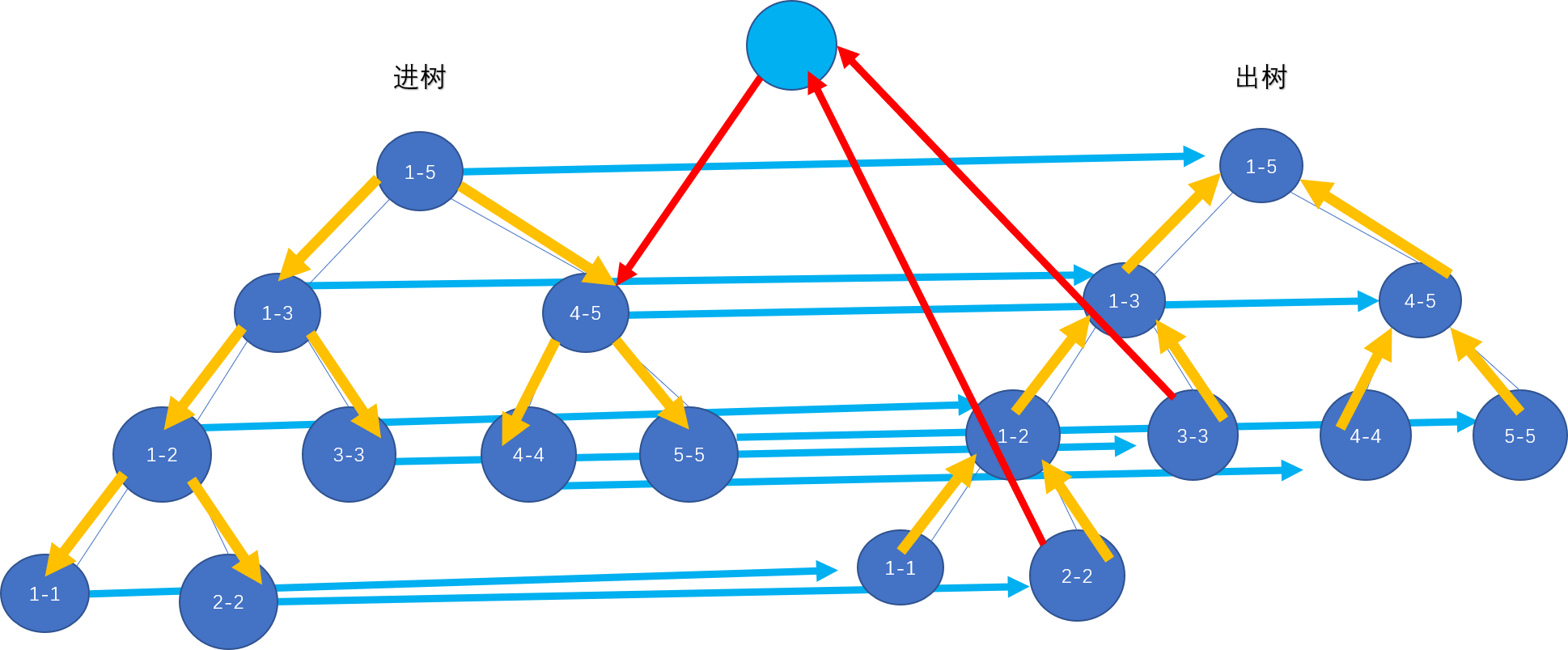
建好图跑Dijkatra就好啦。。。

 

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#define MAXN 4000005
#define MAXM 4000005
using namespace std;
int n,m,p;
int to[4*MAXN],nxt[4*MAXN],pre[4*MAXN],w[4*MAXN],tot_e=0;
void add(int u,int v,int val){
	tot_e++,to[tot_e]=v,nxt[tot_e]=pre[u],w[tot_e]=val,pre[u]=tot_e;
}
int rk[MAXN<<2],ls[MAXN<<2],rs[MAXN<<2],root_a=0,root_b=0,tot=0;//tot:新图的节点编号
struct SegTree_a{//出树,叶向root连边
	void build(int &k,int l,int r){
		k=++tot;
		if(l==r){
			rk[l]=k;//原l接点对应新的k节点
			return ;
		}
		int mid=(l+r)>>1;
		build(ls[k],l,mid);build(rs[k],mid+1,r);
		add(ls[k],k,0),add(rs[k],k,0);
	}
	void update(int l,int r,int L,int R,int x,int y){
		if(l<=L&&R<=r){
			add(x,y,0);
			return ;
		}
		int mid=(L+R)>>1;
		if(l<=mid) update(l,r,L,mid,ls[x],y);
		if(r>mid) update(l,r,mid+1,R,rs[x],y);
	}
}tree_a;
struct Segtree_b{//入树,root向叶连边
	void build(int &k,int l,int r){
		k=++tot;
		if(l==r) return ;
		int mid=(l+r)>>1;
		build(ls[k],l,mid);build(rs[k],mid+1,r);
		add(k,ls[k],0),add(k,rs[k],0);
	}
	void update(int l,int r,int L,int R,int x,int y){
		if(l<=L&&R<=r){
			add(y,x,0);
			return ;
		}
		int mid=(L+R)>>1;
		if(l<=mid) update(l,r,L,mid,ls[x],y);
		if(r>mid) update(l,r,mid+1,R,rs[x],y);
	}
}tree_b;
void ADD(int l,int r,int rt_a,int rt_b){//b连a
	if(l==r){
		add(rt_b,rt_a,0);
		return ;
	}
	int mid=(l+r)>>1;
	ADD(l,mid,ls[rt_a],ls[rt_b]);
	ADD(mid+1,r,rs[rt_a],rs[rt_b]);
}
void ins(int a,int b,int c,int d){
	tree_a.update(a,b,1,n,root_a,++tot);
	add(tot,tot+1,1);
	tree_b.update(c,d,1,n,root_b,++tot);
}
int dis[4*MAXN];
bool vis[4*MAXN];
priority_queue< pair<int,int> > q;//默认大根，插负数
void dijkstra(int p){
	memset(dis,0x7f,sizeof(dis));
	pair<int,int> fr=make_pair(0,rk[p]);
	q.push(fr);
	dis[rk[p]]=0;
	while(!q.empty()){
		int t=q.top().second;
		q.pop();
		if(vis[t]) continue;
		vis[t]=1;
		for(int i=pre[t];i;i=nxt[i]){
			int v=to[i];
			if(dis[v]>dis[t]+w[i]){
                dis[v]=dis[t]+w[i];
                q.push(make_pair(-dis[v],v));
            }
		}
	}
}
int main(){
	scanf("%d%d%d",&n,&m,&p);
	tree_a.build(root_a,1,n);tree_b.build(root_b,1,n);
	ADD(1,n,root_a,root_b);//a,b叶节点对应连边
	for(int i=1,a,b,c,d;i<=m;i++){
		scanf("%d%d%d%d",&a,&b,&c,&d);
		ins(a,b,c,d),ins(c,d,a,b);//区间[a,b],[c,d]连边
	}
	dijkstra(p);
	for(int i=1;i<=n;i++)
		printf("%d
",dis[rk[i]]);
	return 0;
}