Ch07 视觉里程计Ⅰ
1 特征点
- 特征点由两部分组成:关键点和描述子。
- 关键点:在图像中的位置
- 描述子:描述该关键点周围像素的信息,是一个空间向量;只要两个特征点的描述子在向量空间上的距离相近,就可以认为他们是同样的特征点。
2 ORB特征
2.1 组成
- 关键点:Oriented FAST,一种改进的FAST角点
- 描述子:BRIEF
2.2 ORB特征提取步骤
- FAST角点提取:找出图像中的焦点;ORB增加了特征点的主方向,为描述子增加了旋转不变特性。
- BRIEF描述子:对前一步提取出特征点的周围图像区域进行描述。
2.3 FAST角点
2.3.1 思想
- 主要检测局部像素灰度变化明显的地方;
- 如果一个像素与它邻域的像素差别较大,那它更可能是角点
2.3.2 角点检测过程
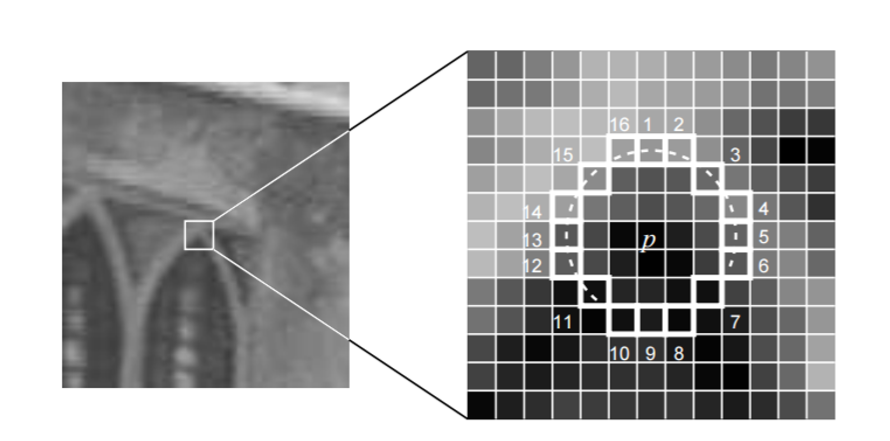
-
在图像中选取像素p,假设它的亮度为Ip
-
设置一个阈值T(比如Ip的20%)
-
以像素p为中心, 选取半径为3的圆上的16个像素点
-
假如选取的圆上,有连续的N个点的亮度大于Ip+T或小于Ip−T,那么像素p可以被认为是特征点 (N 通常取12,即为FAST-12。其它常用的 N 取值为 9 和 11, 他们分别被称为 FAST-9,FAST-11)
-
循环以上四步,对每一个像素执行相同的操作
-
为了更高效的计算,增加了两项技术:
- 预测试操作(对于每个像素,直接检测领域圆上的第1,5,9,13个像素的亮度,三个以上符合条件,才能作为角点)
- 非极大值抑制(在一定区域内仅保留极大值的角点,避免角点集中)
2.3.3 问题及改进
| 问题 | 改进 |
|---|---|
| FAST 特征点数量很大且不确定 | 对原始 FAST 角点分别计算 Harris 响应值,然后选取前 N 个具有最大响应值的角点, 作为最终的角点集合 |
| FAST 角点不具有方向信息 | 特征的旋转是由灰度质心法 |
| 由于它固定取半径为 3 的圆,存在尺度问题 | 尺度不变性由构建图像金字塔,并在金字 塔的每一层上检测角点来实现 |
2.3.4 灰度质心法
质心是指以图像块灰度值作为权重的中心
- 在一个小的图像块 B 中,定义图像块的矩为:
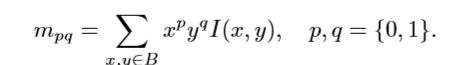
- 通过矩可以找到图像块的质心:
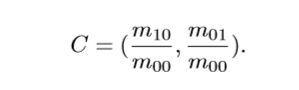
- 连接图像块的几何中心O与质心C,得到一个方向向量OC,于是特征点的方向可以定义为:
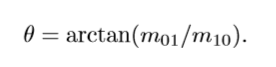
2.4 BRIEF描述子
- 二进制描述子,128维由0,1组成的向量
- 0,附近的像素值小于这个点的像素值;1,为大于
- 随机选点进行比较
3 特征匹配
- 暴力匹配
- 快速近似最近邻
4 对极几何
4.1 对极约束
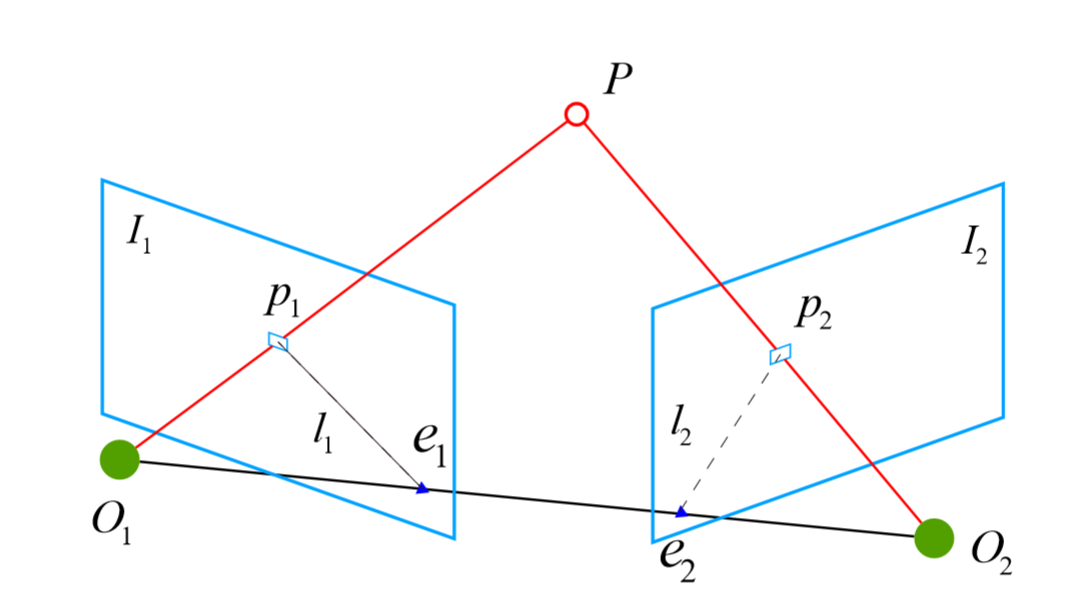
下面这个式子,称为对极约束,几何意义为O1、O2、P在一个平面,对极约束中包含了平移与旋转。
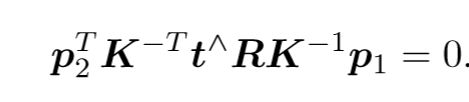
把式子简化得到,本质矩阵E和基础矩阵F
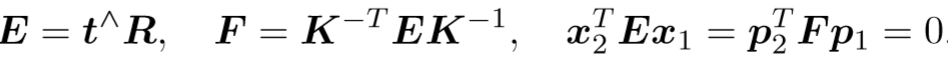
4.2 本质矩阵
4.2.1 性质
- 由平移矩阵t与旋转矩阵R组成,有5个自由度;
- 若一个矩阵式3*3矩阵,则为本质矩阵,则其三个奇异值中两个相同,第三个为0;
4.2.2 本质矩阵求解
- 8点法https://blog.csdn.net/weixin_34060741/article/details/86235942?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-3.add_param_isCf&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-3.add_param_isCf
- 改进8点法
在构造解的方程之前对输入的数据进行适当的归一化。即在形成8点算法的线性方程组之前,图像点的一个简单变换(平移或变尺度)将使这个问题的条件极大地改善,从而提高结果的稳定性。
4.2.3 运动恢复
这个过程是由E的奇异值分解得到的。设E的奇异值分解为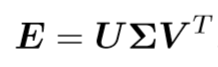
其中U,V都是正交矩阵, 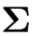 为奇异值矩阵。
为奇异值矩阵。
另外,由线性方程组求得的E可能不满足E的性质,通常做法是把八点法求得的E进行奇异值分解,会得到奇异值矩阵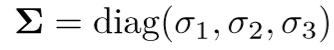 (
(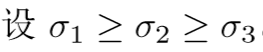
),最后得到
4.3 单应矩阵
5 三角测量
目标:使用三角测量的方法来估计地图点的深度。
定义:通过在两处观察同一个点的夹角,确定该点的距离。
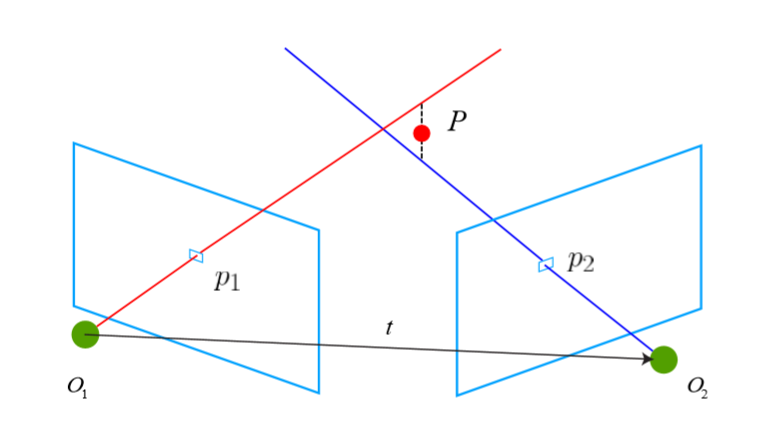
方法:求解两个特征点的深度s1,s2,设x1,x2为两个特征点的归一化坐标
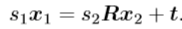
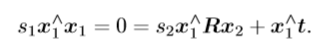
根据上式计算s2,知道了s2,再计算s1。