题目描述
实现函数double Power(double base, int exponent),求base的exponent次方。不得使用库函数,同时不需要考虑大数问题。
示例 1:
输入: 2.00000, 10
输出: 1024.00000
示例 2:
输入: 2.10000, 3
输出: 9.26100
示例 3:
输入: 2.00000, -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25
题目链接:https://leetcode-cn.com/problems/shu-zhi-de-zheng-shu-ci-fang-lcof
朴素解法--思考所有情况
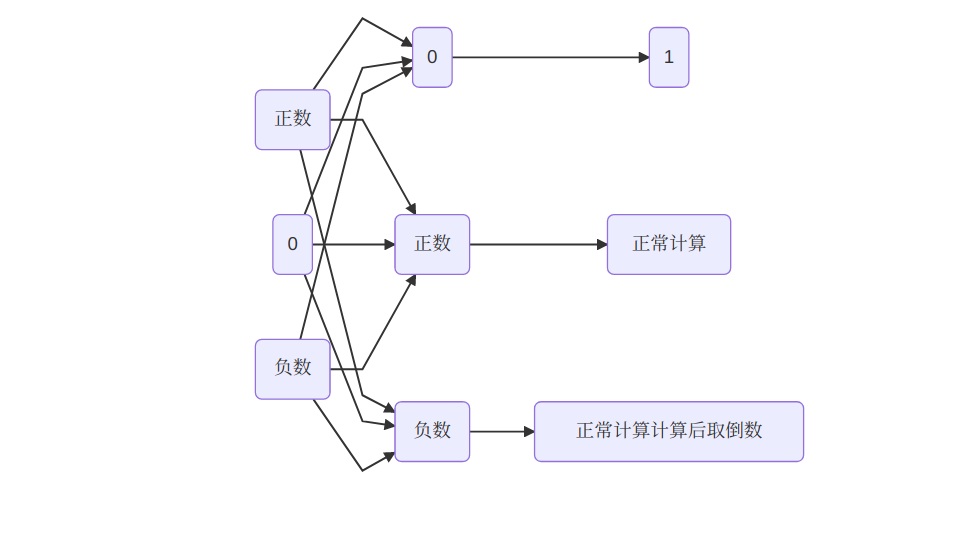
class Solution {
public:
double myPow(double x, int n) {
if(n == 0 || x == 1.00) return 1.00;
int flag = 1;
if(n < 0){
n = -n;
flag = 0;
}
double rst = 1.00;
if(flag){
for(int i = 0 ; i < n;i ++)
rst *= x;
}else{
for(int i = 0; i < n; i++)
rst /= x;
}
return rst;
}
};
快速幂解法
$$
因为base * base = base^2
$$
$$
base^2 * base^2 = base^4
$$
$$
同理 base^4 * base^4 = base^8
$$
对于任意的非负指数可拆成二进制指数,例如
$$
base^{11} = base^1 * base^2 * base^8
$$
注:$[11]{十进制} = [1011]{二进制}$
快速幂模板代码
// int pow(int base,int exp)
// 快速幂函数,返回 base^exp
// base 底数,exp指数
int pow(int base, int exp){
int ans = 1;
while(exp){
if(exp & 0x1){
ans *= base;//如果二进制的最后一位是1,则让ans = ans * base
}
base *= base;//第一次循环,base=base,第二次base = base^2...
exp >>= 1;
}
return ans;
}
本题解答
class Solution {
public:
double myPow(double base, int n) {
double res = 1.0;
int exp = n;
while(exp){
if(exp & 0x01) res *= base;
base *= base;
exp /= 2;
}
return n>0?res:1.0/res;
}
};