不想写什么详细的讲解了...而且也觉得自己很难写过某大佬(大米饼),于是建议把他的 blog 先看一遍,然后自己加了几道题目以及解析...顺便建议看看算法竞赛(蓝皮书)的 0x5A 斜率优化(P294) 部分
这是——大米饼大佬
看完了大米饼同志对斜率优化的介绍,下面我来稍微讲讲对斜率优化dp 的理解
前置知识
- 单调队列(栈)
- 平面直角坐标系
- 直线解析式
- 等式处理
- dp状态设计
- balabala......
理解
其实斜率优化 dp 的原理很简单:
- 根据题目(斜率优化 dp 的题目一般都很裸)的 题意 以及 数据范围 先根据设计一个状态出来,当做 dp 数组。
- 根据已经设计好的 dp 状态设计一个状态转移方程,如果设计失败则跳回第一步,重新设计 dp 状态。
- 在第二步完成后,我们一般可以得到这样的一个式子:$ Fi = Fj +$ $(一个表达式)$
- 根据设计的状态做一些乱七八糟的东西(比如说将式子展开啦,移项啦...这些大米饼讲的应该挺清楚的吧)。
- 在第四步中,我们在将式子展开后,把下标中同时带有 i、j 的项(注意这里是项,如 Si*Sj)移到等式的左边。
- 然后我们就可以得到一个 $b + k x = y$ 形态的一般式(大米饼是这么叫的),其中等式左边下标带有 i 的变量(注意这里是变量,如Si)作为 k ,下标带有 j 的变量作为 x ,等式右边下标带有 j 的变量作为 y ,至于等式右边那些下标只带有 i 的变量我们不去管它,因为 i 在当前对于 Fi 的计算中相当于一个常量,对结果的影响一定。
- 然后我们发现这时候我们就可以得到点 (x, y) 了,那么我们就基本上已经完成了这道 斜率优化 dp 题了。
- 那么我们是要根据题意让 Fi (也就是一般式中的 b )取到最小(大)值,那么我们的任务也就转化成了过一个点,画一条斜率为 k 的射线,令其与 y 轴的截距(与 y 轴的交点和原点的距离叫做截距)最小(大)。
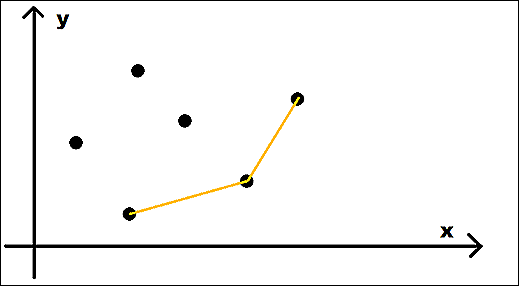
做完这些工作之后,你把所有的点画到平面直角坐标系上,就可以看到这样的一条折线(假设我们现在求的是 Fi 的最小值):
没错,这就是可能有用的点形成的像凸包一样的东西(凸壳)。那为什么这些点形成的折线一定是向下凸起的呢?
我们可以想想一下,如果折线内凹,那么引起内凹的那个点可能成为有用点吗?不可能,因为经过该点的斜率为 k 的直线与 y 轴的截距必然不会比它旁边两个点的截距要小
那么我们在来考虑一下,如果我们要求的是 Fi 的最大值呢?那么我们只要让折线向上凸起就好了(维护上凸性)。
对了对了!还有一点蛮重要的。那就是斜率优化可行性判定的标准(我自己口胡的): 我们在上面的步骤中会处理出一个一般式中的 k 吗?那个 k 要满足单调性,
不然是没办法用双端队列(单调队列)维护的。
然后这里有一些题目
题目
洛谷P4072 [SDOI2016]征途
分析
首先你在做这题之前最好已经做过了 洛谷P3648 [APIO2014]序列分割 这道题(上面的 T6)。
这道题你只要一直推推推把式子推出来,然后发现 $ans = m * sum_{i=1}^{m}a[i]^{2} - sum[n]^{2}$ ,
那么你就能知道我们要求的是 $min{sum_{i=1}^{m}a[i]^{2}}$ (这就是序列分割啊),最后答案处理一下就好了。
代码
1 //by Judge 2 #include<iostream> 3 #include<cstdio> 4 #define ll long long 5 using namespace std; 6 const int M=3111; 7 #define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) 8 char buf[1<<21],*p1=buf,*p2=buf; 9 inline int read(){ 10 int x=0,f=1; char c=getchar(); 11 for(;!isdigit(c);c=getchar()) if(c=='-') f=-1; 12 for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x*f; 13 } 14 ll n,m,sum[M],g[M],f[M],q[M],head,tail; 15 inline double Rate(ll i,ll j){ 16 if(sum[i]==sum[j]) return -1e9; 17 return (g[j]-g[i]+sum[j]*sum[j]-sum[i]*sum[i])/(1.0*sum[j]-sum[i]); 18 } 19 signed main(){ 20 n=read(),m=read(); 21 for(int i=1;i<=n;++i) 22 sum[i]=sum[i-1]+read(),g[i]=sum[i]*sum[i]; 23 for(int k=2,i;k<=m;++k){ 24 head=tail=0; 25 for(i=1;i<=n;++i){ 26 while(head<tail && Rate(q[head+1],q[head])<=2*sum[i]) ++head; 27 f[i]=g[q[head]]+(sum[i]-sum[q[head]])*(sum[i]-sum[q[head]]); 28 while(head<tail && Rate(q[tail-1],q[tail])>=Rate(q[tail],i)) --tail; q[++tail]=i; 29 } swap(f,g); 30 } printf("%lld ",g[n]*m-sum[n]*sum[n]); return 0; 31 }
洛谷P4360 [CEOI2004]锯木厂选址
分析
首先这道题其实与仓库建设类似,同时(可以算是)综合了序列分割...但是数据的处理有点麻烦(甚至还有点坑,比如 d 和 w 搞反了然后样例里面 d 、w 读入雷同...)
这题偷懒一点就是 抄 综合 一下序列分割这道题,将它作为模板,K 设成 3 ,n 要加一,然后常规做就好了。推式子也不是很麻烦,和仓库建设一样的套路
代码
1 //by Judge 2 #include<iostream> 3 #include<cstdio> 4 #define int long long 5 #define ll long long 6 using namespace std; 7 const int M=5e4+111; 8 #ifdef ONLINE_JUDGE 9 #define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) 10 #endif 11 char buf[1<<21],*p1=buf,*p2=buf; 12 inline int read(){ 13 int x=0,f=1; char c=getchar(); 14 for(;!isdigit(c);c=getchar()) if(c=='-') f=-1; 15 for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x*f; 16 } 17 ll n,K,x[M],w[M],s[M],g[M],f[M],q[M],head,tail; 18 inline double Rate(ll i,ll j){ 19 if(w[i]==w[j]) return -1e18; 20 return (g[j]-g[i]+s[j]-s[i])/(1.0*w[j]-w[i]); 21 } 22 int las[M]; 23 signed main(){ 24 n=read()+1; 25 for(int i=1;i<=n;++i) 26 (i<n)&&(w[i]=read(),x[i+1]=x[i]+read()), 27 s[i]=s[i-1]+x[i]*w[i],w[i]+=w[i-1],g[i]=1e18; 28 for(int k=1,i;k<=3;++k){ 29 head=tail=0; 30 for(i=1;i<=n;++i){ 31 while(head<tail && Rate(q[head+1],q[head])<=x[i]) ++head; 32 f[i]=g[q[head]]+x[i]*(w[i-1]-w[q[head]])-s[i-1]+s[q[head]]; 33 while(head<tail && Rate(q[tail-1],q[tail])>=Rate(q[tail],i)) --tail; q[++tail]=i; 34 } swap(f,g); 35 } printf("%lld ",g[n]); return 0; 36 }
其他题...咳咳(来自刷题慢者的尴尬...做一道题都要在黑板上墨迹个半天QwQ)
洛谷P2365 任务安排
分析
这道题...其实蛮(不)简单的啦。这题你要消除后效性才能做(其实这是一道经典题目,算法竞赛上都有)。
一开始我们让 $1~n$ 这一整段为一个区间,现在我们考虑当前将$ 1 ~ i $这一区间分为一段,
那么后面所有的任务(以及 $1 ~ i$ 这段区间)必定会多加上 S 时间的代价(即 $S * (C_{n}-C_{1})$,其中 C 为 c 数组的前缀和),而后面区间的分割并不会对前面的分割造成影响。
同理, i 之后的区间我们也可以按照这个思路分下去,以消除后效性。那么我们现在就可以列出状态转移方程:$ Fi = Fj + (Cj-Ci)*xi + (Cn-Cj)*S $ 然后展开式子移项后我们就可以斜率优化了。
代码
1 //by Judge 2 #include<iostream> 3 #include<cstdio> 4 #define mid (l+r>>1) 5 #define ll long long 6 using namespace std; 7 const int M=1e6+111; 8 #ifdef online_judge 9 #define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) 10 #endif 11 char buf[1<<21],*p1=buf,*p2=buf; 12 inline int read(){ 13 int x=0,f=1; char c=getchar(); 14 for(;!isdigit(c);c=getchar()) if(c=='-') f=-1; 15 for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x*f; 16 } 17 ll n,S,head,tail,q[M],t[M],c[M],f[M]; 18 inline double X(int i){ return c[i]; } 19 inline double Y(int i){ return f[i]-c[i]*S; } 20 inline double Rate(int i,int j){ return (Y(j)-Y(i))/(X(j)-X(i)); } 21 signed main(){ 22 n=read(),S=read(); 23 for(int i=1;i<=n;++i) t[i]=t[i-1]+read(),c[i]=c[i-1]+read(); 24 for(int i=1;i<=n;++i){ 25 while(head<tail && Rate(q[head+1],q[head])<=t[i]) ++head; 26 f[i]=f[q[head]]+(c[n]-c[q[head]])*S+(c[i]-c[q[head]])*t[i]; 27 while(head<tail && Rate(q[tail],q[tail-1])>=Rate(i,q[tail])) --tail; q[++tail]=i; 28 } printf("%lld ",f[n]); return 0; 29 }
洛谷CF311B Cats Transport
分析
没什么好分析的和上面一样公式套取就好了(套个鬼哦)。
咳咳。首先你要分析怎么把这道题硬设计出 dp 状态。那么我们来看看,其实路程对于问题的影响并不显得有多么重要,于是我们可以考虑消除这个影响。
如何消除?题目中说,饲养员(说好的铲屎官...)到达猫的位置所需时间就是距离 $X_{i}$,那么其实猫在 $T_{i}$ 的时间开始等待,而饲养员出发时间对于我们要求的答案是没有影响的(何况题目中说了饲养员出发时间可以为负数),
那么我们可以让猫开始等待的时间 $T_{i}$ 减去路程的影响 $X_{i}$ (感性理解一下),然后我们再对减完 $X_{i}$ 的 $T_{i}$ 排一下序就好了。
这里如何解释?emmm...思考一下,一个饲养员出发必然是会接回所有正在等待的猫对吧(猫不可能给下一个人接,那样不会更优,而上一个人能接回去早接回去了)
咳咳...那么这个饲养员能接到哪些猫呢?当然是 $T-X$(等待开始时间减去路程) 小于等于饲养员出发时间的所有猫咯!于是解释完毕。
排完序后,可以看出我们要接到第 i 只猫的话,它前面的猫我们都可以接到(因为在这只猫之前的猫早就开始等待了)。
于是这道题就变成了分割序列...(切 p 刀,但是注意这里是最多切 p 刀,不一定切完,有的饲养员可以不动的嘛)。
咳咳,但是转移方程是不一样的:$ F_{i} = F_{j} + (T_{i}-T_{i-1}) * (i-j) - (T_{i}-T_{j}) $ (T 是上文中 $T-X$ 的前缀和数组)
那么这个表达式原来的样子是:$ F_{i} = MIN{ F_{j} + sum_{k=j}^{i} ( t_{i}-t_{k} ) }$ (这里的 t 是上文中的 $T-X$ 数组)
然后我们就非常愉快的 ctrl+C 、 ctrl+V 将之前打好的序列分割板子弄了下来开始了新一轮的斜率优化。
代码
1 //by Judge 2 #include<algorithm> 3 #include<iostream> 4 #include<cstdio> 5 #define ll long long 6 using namespace std; 7 const int M=1e5+111; 8 const ll inf=1e16+7; 9 #ifdef ONLINE_JUDGE 10 #define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) 11 #endif 12 char buf[1<<21],*p1=buf,*p2=buf; 13 inline int read(){ 14 int x=0,f=1; char c=getchar(); 15 for(;!isdigit(c);c=getchar()) if(c=='-') f=-1; 16 for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x*f; 17 } 18 ll n,m,p,ans=inf,d[M],a[M],g[M],f[M],q[M],head,tail; 19 inline double Y(int i){ return g[i]+a[i]; } 20 inline double X(int i){ return i; } 21 inline double Rate(ll i,ll j){ return (Y(j)-Y(i))/(X(j)-X(i)); } 22 signed main(){ 23 n=read(),m=read(),p=read(); 24 for(int i=2;i<=n;++i) d[i]=d[i-1]+read(); 25 for(int i=1,x,y;i<=m;++i) x=read(),y=read(),a[i]=y-d[x],g[i]=inf; 26 sort(a+1,a+m+1); for(int i=2;i<=m;++i) a[i]+=a[i-1]; 27 for(int k=1,i;k<=p;++k){ 28 head=tail=0; 29 for(i=1;i<=m;++i){ 30 while(head<tail && Rate(q[head+1],q[head])<=a[i]-a[i-1]) ++head; 31 f[i]=g[q[head]]+(a[i]-a[i-1])*(i-q[head])-a[i]+a[q[head]]; 32 while(head<tail && Rate(q[tail-1],q[tail])>=Rate(q[tail],i)) --tail; q[++tail]=i; 33 } swap(f,g); ans=min(ans,g[m]); 34 } printf("%lld ",ans); return 0; 35 }
BinamotoOJ P4709: [Jsoi2011]柠檬
分析
这题就是斜率优化裸题啊! 这道题非常值得一做,因为它深刻的告诉了我们,斜率优化可以用单调栈维护!
首先这题就是让我们吧一个序列分成若干份,然后根据公式计算最大值(注意是最大值,维护折线上凸性)
我们可以非常轻松的看出我们要取的一段区间的左右端点必然是相同的颜色,且我们选择的颜色就是左右端点的颜色。
(我们每一段只能选一种颜色,那么如果左右端点不同,我们完全可以将与选择的颜色不同的那一端隔离出来分到另一段区间里,那样更优)
于是我们在读入时维护一个 las 指针,指向当前颜色上一次出现的位置,同时记录每个点之前与该点颜色相同的点有多少个(用 S 数组记录)。
然后我们将所有颜色第一次出现时的位置压入单调栈,接着就可以开始 dp 了。
那么 dp 转移式就是 : $$ f[i] = f[j-1] + (s[i]-s[j]+1)*a[i] $$ (其中 i 、j 位置的贝壳颜色相同)
斜率式就是: $$ f[i] + 2*a[i]*s[i]*s[j] = f[j-1] + a[i]*s[j]^{2} - 2*a[i]*s[j] + 2*a[i]*s[i]+a[i]*s[i]^{2}+a[i] $$
$$ X(i)= s[j] , K=2*a[i]*s[i] $$
$$ Y(i)= f[j-1] + a[i]*s[j]^{2} - 2*a[i]*s[j] $$
代码
1 //by Judge 2 #include<iostream> 3 #include<cstdio> 4 #include<queue> 5 #define ll long long 6 using namespace std; 7 const int M=1e5+111; 8 //#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) 9 char buf[1<<21],*p1=buf,*p2=buf; 10 inline int read(){ 11 int x=0,f=1; char c=getchar(); 12 for(;!isdigit(c);c=getchar()) if(c=='-') f=-1; 13 for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x*f; 14 } 15 ll n,ans,las[M],a[M],s[M],f[M],top[M]; vector<int> q[M]; 16 inline long double X(int i){ return s[i]; } 17 inline long double Y(int i){ return f[i-1]+a[i]*s[i]*(s[i]-2); } 18 inline long double Rate(ll i,ll j){ return (Y(j)-Y(i))/(X(j)-X(i)); } 19 signed main(){ 20 n=read(); ll p,x,y; 21 for(int i=1;i<=n;++i) a[i]=read(),s[i]=s[las[a[i]]]+1,las[a[i]]=i;; 22 for(int i=1;i<=n;++i) if(las[a[i]]) q[a[i]].push_back(i),las[a[i]]=0; 23 for(int i=1;i<=n;++i){ p=a[i]; 24 while(top[p]>1 && Rate(q[p][top[p]-1],q[p][top[p]])<=Rate(q[p][top[p]],i)) --top[p],q[p].pop_back(); 25 ++top[p],q[p].push_back(i); 26 while(top[p]>1 && Rate(q[p][top[p]-1],q[p][top[p]])<=2*p*s[i]) --top[p],q[p].pop_back(); 27 f[i]=f[q[p][top[p]]-1]+(s[i]-s[q[p][top[p]]]+1)*(s[i]-s[q[p][top[p]]]+1)*p; 28 } printf("%lld ",f[n]); return 0; 29 }