非旋 $treap$ (FHQ treap)的简单入门
前置技能
建议在掌握普通 treap 以及 左偏堆(也就是可并堆)食用本blog
原理
以随机数维护平衡,使树高期望为logn级别, FHQ 不依靠旋转,只有两个核心操作merge(合并)和split(拆分)
所谓随机数维护平衡就是给每个节点一个随机值 key (下文中没有加随机的就代表是真实权值),
然后整棵树中 key 值要满足小(大)根堆的性质(也就是heap),
同时也要满足平衡树(tree)的性质(也就是每个节点左子树内节点真实权值小于它,右子树相反)
然后这个玩意儿就有了一个草率的名字:treap (tree 和 heap 的结合体)
结构体变量介绍

1 int Rand() { //伪随机函数,能让代码稍微变快 2 static int seed=703; 3 return seed=int(seed*48271LL%(~0u>>1)); 4 } 5 struct Node { 6 int val,key,siz,ch[2]; 7 // val 真实权值,key 随机权值,siz 子树大小 , ch 左右子节点 8 void clear() { //清空操作 9 ch[0]=ch[1]=siz=val=key=0; 10 } 11 } t[M]; 12 int update(int now){ //更新操作 13 t[now].siz=t[t[now].ch[0]].siz+t[t[now].ch[1]].siz+1; 14 }
核心操作
merge操作
模型实现
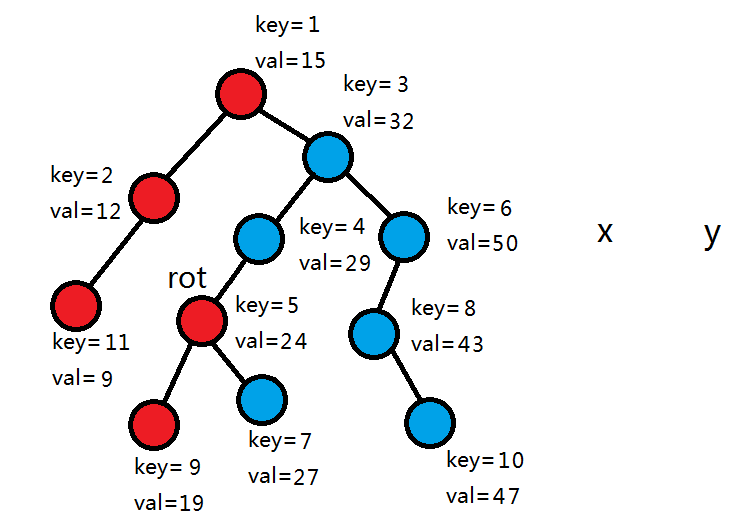
假设有两颗子树x,y,且 x 的所有节点的值都小于 y 的所有节点的值,随机权值 key 都以小根堆的形式存储。
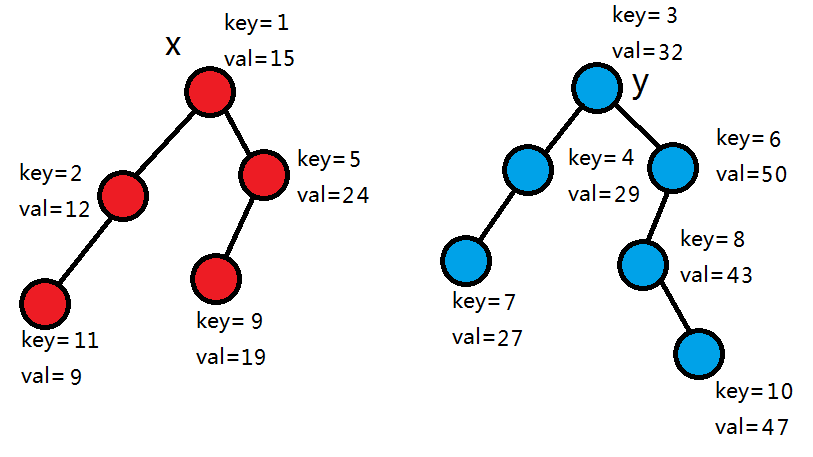
此时要合并 x , y 。我们先比较它们的根的随机权值,发现1<3,因为要满足小根堆性质,于是 x 的左子树全部不变,让它的右子树继续和 y 合并。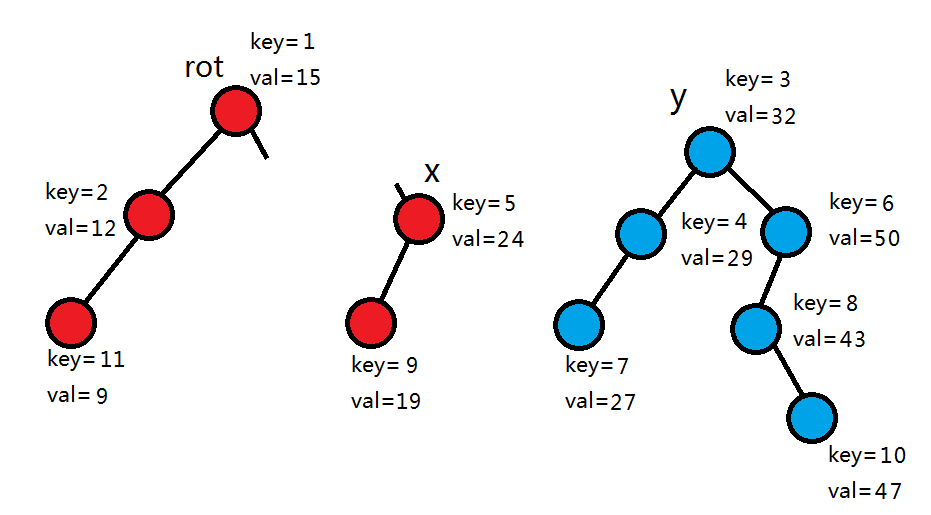
这时我们发现,随机权值 key 5>3,所以 y 接到 rot 的下方,成为 rot 的右儿子,y的右子树全部不变,让y的左子树继续和x合并(以满足平衡树的性质)。
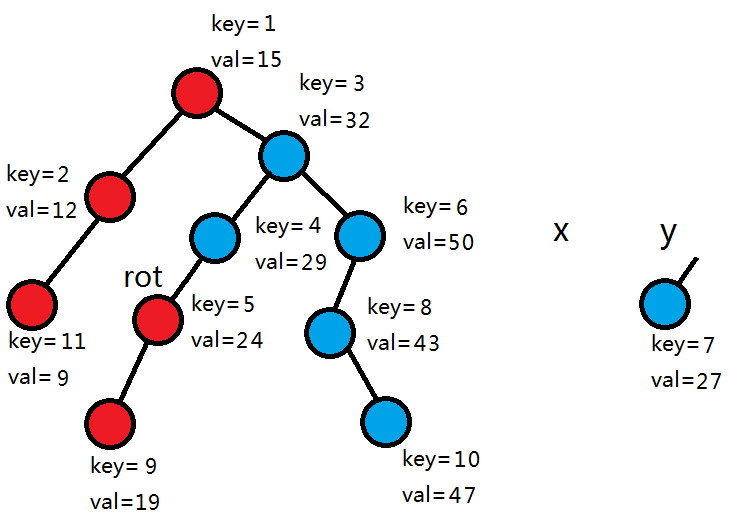
由于5>4,所以y和y的右子树作为rot的左儿子,y的左子树继续和x合并。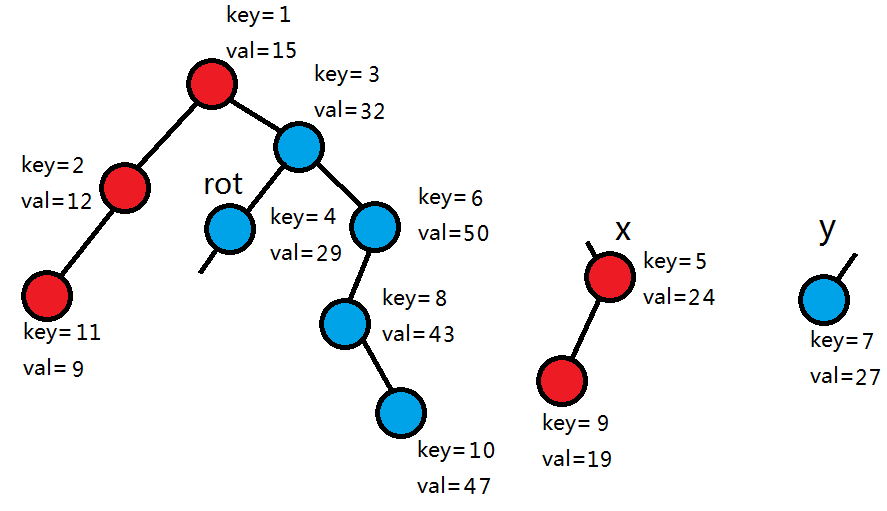
5<7,所以接入x和它的左子树作为rot的左儿子。
至此,我们发现 x 为 0 ,所以直接返回 y ,合并结束。
代码实现

1 int merge(int u,int v) { // 此时 u 中节点权值均小于 v 中节点权值 2 if(!u || !v) return u|v; //某节点为空,直接返回另一节点 3 if(t[u].key<t[v].key) { //以此满足 heap 性质 4 t[u].ch[1]=merge(t[u].ch[1],v); // u 右子节点与 v 合并, 以满足平衡树性质 5 update(u); return u; 6 } else { 7 t[v].ch[0]=merge(u,t[v].ch[0]); // u 与 v 左子节点合并, 以满足平衡树性质 8 update(v); return v; 9 } 10 }
split操作
split有两种拆分方式:
1. 按权值大小拆分
2. 按排名大小拆分。
模型实现
1.按权值split
首先得有个基准值 a ,即权值小于等于 a 的节点全部进入左树(下图中会将此类节点染红),大于a的节点全部进入右树(下图中会将此类节点染蓝)。这里以a=25为例。
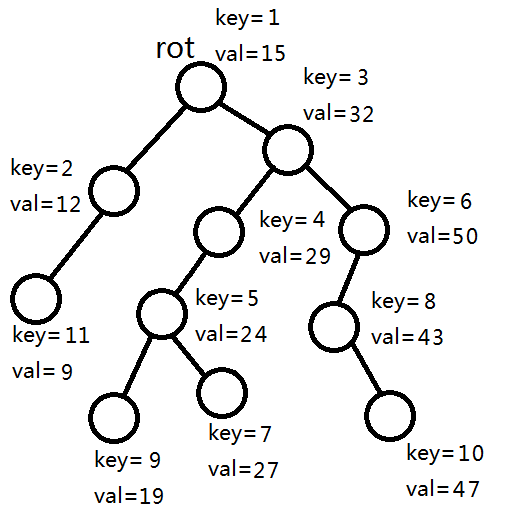
首先,发现rot的权值=15<25,由平衡树的性质可知,rot的左子树所有节点权值一定小于25,所以rot和它的的左子树全部进入左树,继续拆分rot的右子树。
32>25,所以 rot 和它的右子树全部进入右树,继续拆分 rot 的左子树。

29>25,同上。
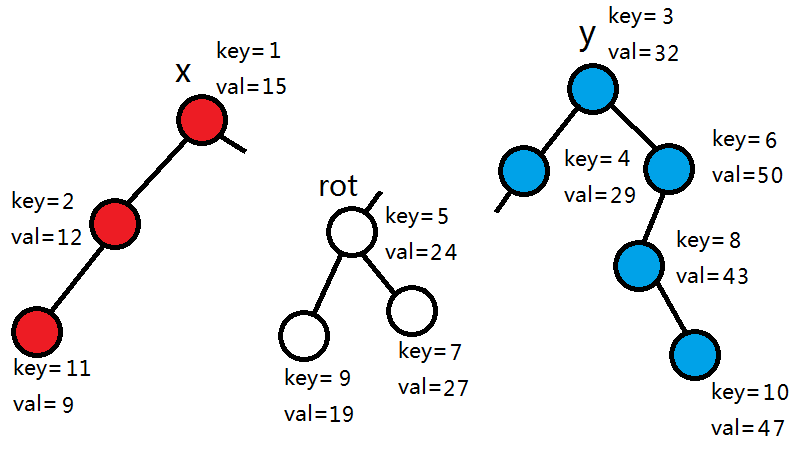
24<25,所以拆分右子树。
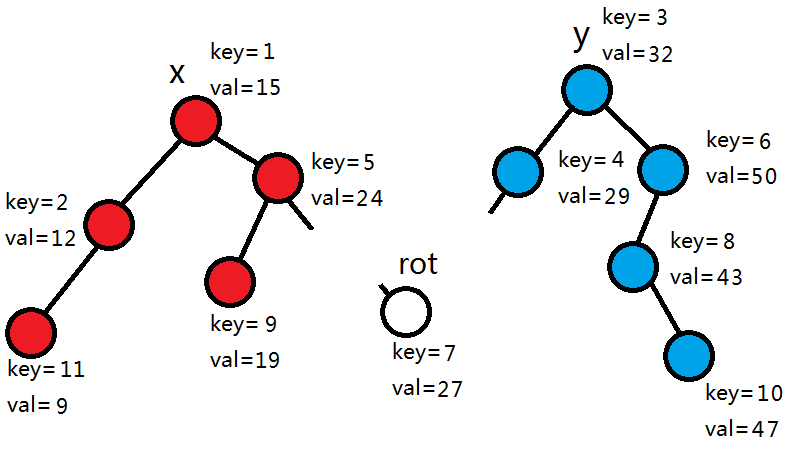
27>25,所以拆分左子树。
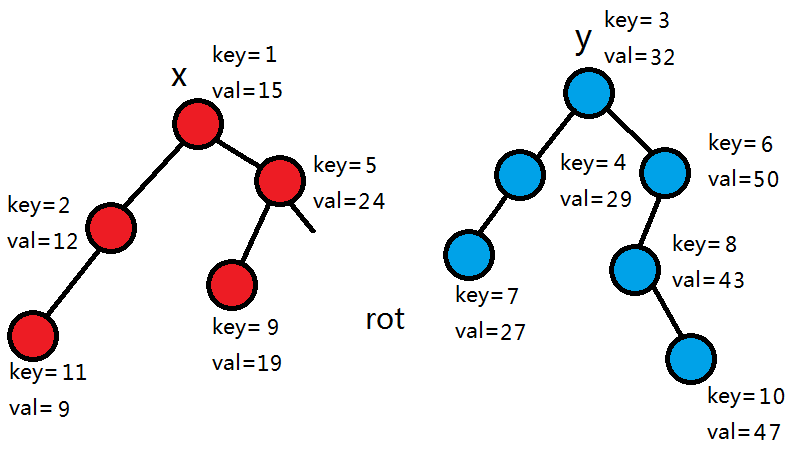
发现此时rot为0,所以拆分完毕,返回。
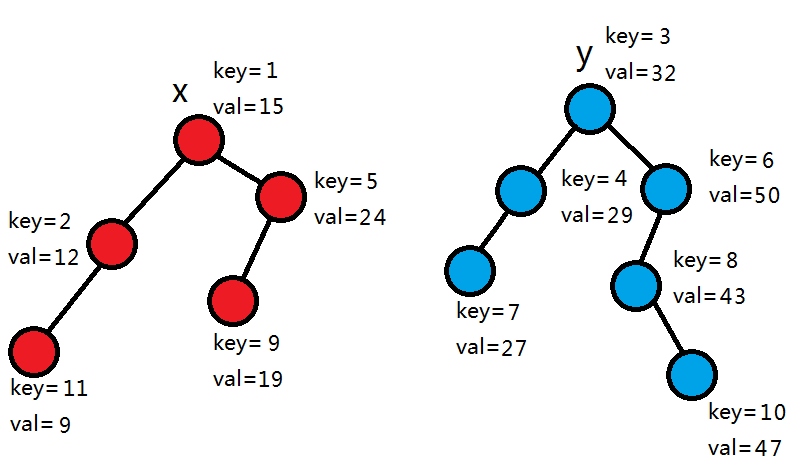
2.按排名split
就是把前 k 个节点拆入左树,其它节点拆入右树。这里以k=5为例。
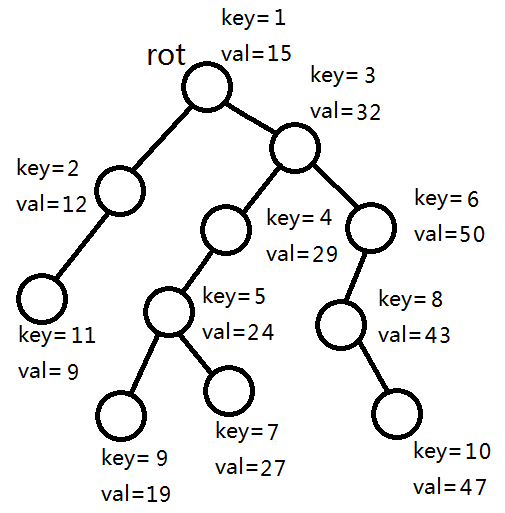
rot的左子树的siz+1=3<5,所以rot和它的左子树进入左树,其他节点拆分5-3=2个节点进入左树。
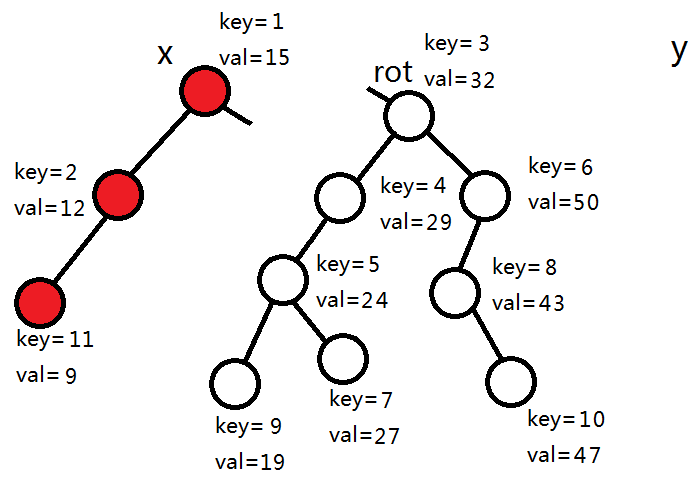
4+1>2,所以rot和右子树进入右树,其它节点继续拆分出2个节点进入左树。

3+1>2,同上。
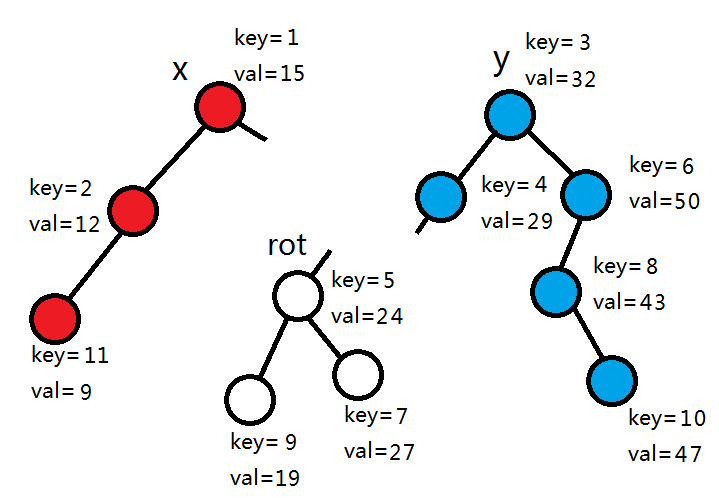
1+1=2,所以rot和左子树进入左树,其它节点继续拆分2-2=0个节点进入左树。
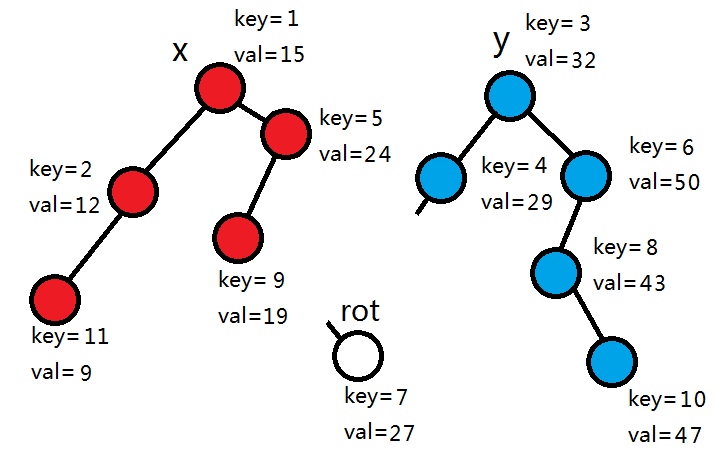
1+0>0,所以rot和右子树进入右树,其它节点继续拆分0个节点进入左树。
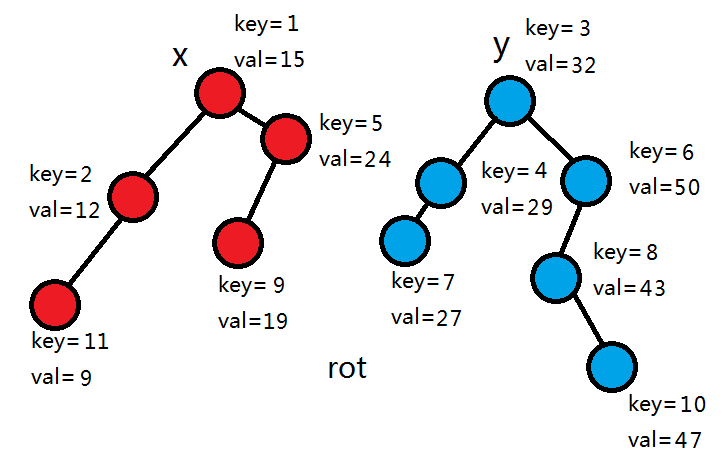
rot为0,拆分结束。
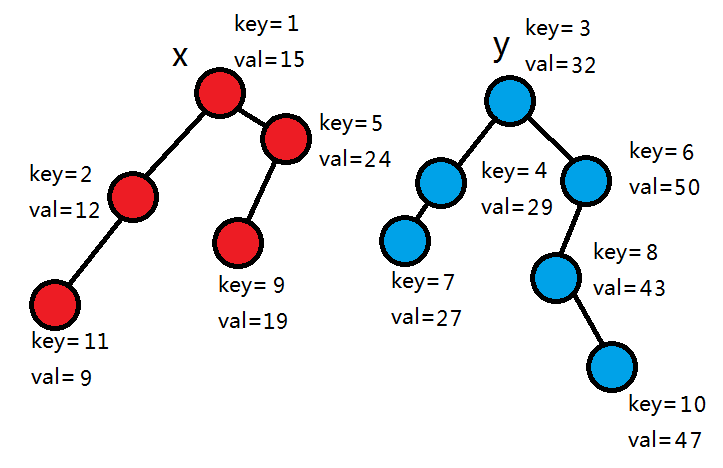
代码实现
1.按权值split

1 void split_val(int now,int k,int& x,int& y) { 2 if(!now) return (void)(x=y=0); //节点为空, return 3 if(t[now].val<=k) //当前节点和它的左子树都满足进入左树的条件 4 x=now,split_val(t[now].ch[1],k,t[now].ch[1],y); 5 else //当前节点和它的右子树都满足进入右树的条件 6 y=now,split_val(t[now].ch[0],k,x,t[now].ch[0]); 7 update(now); 8 }
2.按排名split

1 void split_k(int now,int k,int& x,int& y) { //与按权值 split 类似 2 if(!now) return (void)(x=y=0); 3 update(now); 4 if(t[t[now].ch[0]].siz<k) 5 x=now,split_k(t[now].ch[1],k-t[t[now].ch[0]].siz-1,t[now].ch[1],y); 6 else 7 y=now,split_k(t[now].ch[0],k,x,t[now].ch[0]); 8 update(now); 9 }
其他操作
FHQ treap 的核心操作只有 merge 和 split 两个,其他操作都是基于这两个操作实现的。
插入
插入权值为 x 的节点时,先新建一个节点,再以 x 为界按权值 split 整棵树为a,b,再按顺序 merge a,x,b。
代码实现

1 void ins(int x) { 2 int u,a,b; 3 t[u=++cnt].key=Rand(); 4 t[u].val=x,t[u].siz=1; 5 split_val(root,x,a,b); 6 root=merge(merge(a,u),b); 7 }
删除
要删除x,先将整棵树以 x-1 为界按权值split 成a和b,再将 b 以 1 为界 按排名split 成c和d,则 c 就是要删除的节点。最后按顺序merge a,b,d。
(当然,这是在要删除节点必定存在的情况下才能进行的操作,不存在的情况请自行脑补)
代码实现

1 void del(int x) { 2 int a,b,c,d; 3 split_val(root,x-1,a,b); 4 split_k(b,1,c,d); 5 t[c].clear(),root=merge(a,d); 6 }
查询 x 的排名
先将整棵树以x-1按权值split成a和b,则a的siz+1即为x的排名。
代码实现

1 int get_rank(int x) { 2 int a,b,c; 3 split_val(root,x-1,a,b); 4 c=t[a].siz+1; 5 root=merge(a,b); 6 return c; 7 }
查询排名为 k 的值
先split出整棵树前k-1小节点,则右树最小节点即为所求节点,再次split 即可。
代码实现

1 int get_val(int& now,int x) { 2 int a,b,c,d,e; 3 split_k(now,x-1,a,b); 4 split_k(b,1,c,d); 5 e=t[c].val; 6 now=merge(a,merge(c,d)); 7 return e; 8 }
查x前驱
将整棵树以x-1按权值split,左树中最大节点即为所求节点,转入第x小值问题。
代码实现

1 int pre(int x) { 2 int a,b,c; 3 split_val(root,x-1,a,b); 4 c=get_val(a,t[a].siz); 5 root=merge(a,b); 6 return c; 7 }
查x后继
将整棵树以x按权值split,右树中最小节点即为所求节点,转入第x小值问题。
代码实现

1 int sub(int x) { 2 int a,b,c; 3 split_val(root,x,a,b); 4 c=get_val(b,1); 5 root=merge(a,b); 6 return c; 7 }
非旋 Treap的其他作用
非旋 trap 是支持区间操作的,具体其实就是你把原来的一棵树 split 成 3 棵树($1~l-1,l~r,r+1~n$),然后 我们对中间那棵树进行操作即可,具体代码不附上了
例题
代码

1 //by Judge 2 #include<iostream> 3 #include<cstdio> 4 using namespace std; 5 const int M=1e5+111; 6 #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) 7 char buf[1<<21],*p1=buf,*p2=buf; 8 inline int read(){ 9 #define num ch-'0' 10 char ch;bool flag=0;int res; 11 while(!isdigit(ch=getc())) 12 (ch=='-')&&(flag=true); 13 for(res=num;isdigit(ch=getc());res=res*10+num); 14 (flag)&&(res=-res); 15 #undef num 16 return res; 17 } 18 char sr[1<<21],z[20];int C=-1,Z; 19 inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;} 20 inline void print(int x){ 21 if(C>1<<20)Ot();if(x<0)sr[++C]=45,x=-x; 22 while(z[++Z]=x%10+48,x/=10); 23 while(sr[++C]=z[Z],--Z);sr[++C]=' '; 24 } 25 int n,cnt,root; 26 int Rand() { 27 static int seed=703; 28 return seed=int(seed*48271LL%(~0u>>1)); 29 } 30 struct Node { 31 int val,key,siz,ch[2]; 32 void clear() { 33 ch[0]=ch[1]=siz=val=key=0; 34 } 35 } t[M]; 36 int update(int now){ 37 t[now].siz=t[t[now].ch[0]].siz+t[t[now].ch[1]].siz+1; 38 } 39 int merge(int u,int v) { 40 if(!u || !v) return u|v; 41 if(t[u].key<t[v].key) { 42 t[u].ch[1]=merge(t[u].ch[1],v); 43 update(u); return u; 44 } else { 45 t[v].ch[0]=merge(u,t[v].ch[0]); 46 update(v); return v; 47 } 48 } 49 void split_val(int now,int k,int& x,int& y) { 50 if(!now) return (void)(x=y=0); 51 if(t[now].val<=k) 52 x=now,split_val(t[now].ch[1],k,t[now].ch[1],y); 53 else 54 y=now,split_val(t[now].ch[0],k,x,t[now].ch[0]); 55 update(now); 56 } 57 void split_k(int now,int k,int& x,int& y) { 58 if(!now) return (void)(x=y=0); 59 update(now); 60 if(t[t[now].ch[0]].siz<k) 61 x=now,split_k(t[now].ch[1],k-t[t[now].ch[0]].siz-1,t[now].ch[1],y); 62 else 63 y=now,split_k(t[now].ch[0],k,x,t[now].ch[0]); 64 update(now); 65 } 66 void ins(int x) { 67 int u,a,b; 68 t[u=++cnt].key=Rand(); 69 t[u].val=x,t[u].siz=1; 70 split_val(root,x,a,b); 71 root=merge(merge(a,u),b); 72 } 73 void del(int x) { 74 int a,b,c,d; 75 split_val(root,x-1,a,b); 76 split_k(b,1,c,d); 77 t[c].clear(),root=merge(a,d); 78 } 79 int get_rank(int x) { 80 int a,b,c; 81 split_val(root,x-1,a,b); 82 c=t[a].siz+1; 83 root=merge(a,b); 84 return c; 85 } 86 int get_val(int& now,int x) { 87 int a,b,c,d,e; 88 split_k(now,x-1,a,b); 89 split_k(b,1,c,d); 90 e=t[c].val; 91 now=merge(a,merge(c,d)); 92 return e; 93 } 94 int pre(int x) { 95 int a,b,c; 96 split_val(root,x-1,a,b); 97 c=get_val(a,t[a].siz); 98 root=merge(a,b); 99 return c; 100 } 101 int sub(int x) { 102 int a,b,c; 103 split_val(root,x,a,b); 104 c=get_val(b,1); 105 root=merge(a,b); 106 return c; 107 } 108 int main() { 109 n=read(); int opt,x; 110 while(n--){ 111 opt=read(),x=read(); 112 switch(opt){ 113 case 1: ins(x); break; 114 case 2: del(x); break; 115 case 3: print(get_rank(x)); break; 116 case 4: print(get_val(root,x)); break; 117 case 5: print(pre(x)); break; 118 case 6: print(sub(x)); break; 119 } 120 } Ot(); return 0; 121 }
然后这是压过行了的:

1 //by Judge 2 #include<iostream> 3 #include<cstdio> 4 using namespace std; 5 const int M=1e5+111; 6 #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) 7 char buf[1<<21],*p1=buf,*p2=buf; 8 inline int read(){ 9 #define num ch-'0' 10 char ch;bool flag=0;int res; 11 while(!isdigit(ch=getc())) 12 (ch=='-')&&(flag=true); 13 for(res=num;isdigit(ch=getc());res=res*10+num); 14 (flag)&&(res=-res); 15 #undef num 16 return res; 17 } 18 char sr[1<<21],z[20];int C=-1,Z; 19 inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;} 20 inline void print(int x){ 21 if(C>1<<20)Ot();if(x<0)sr[++C]=45,x=-x; 22 while(z[++Z]=x%10+48,x/=10); 23 while(sr[++C]=z[Z],--Z);sr[++C]=' '; 24 } 25 int n,cnt,root; 26 struct Node { 27 int val,key,siz,ch[2]; 28 void clear() { ch[0]=ch[1]=siz=val=key=0; } 29 } t[M]; 30 int Rand() { static int seed=703; return seed=int(seed*48271LL%(~0u>>1)); } 31 int update(int now){ t[now].siz=t[t[now].ch[0]].siz+t[t[now].ch[1]].siz+1; } 32 int merge(int u,int v) { 33 if(!u || !v) return u|v; 34 if(t[u].key<t[v].key) { t[u].ch[1]=merge(t[u].ch[1],v),update(u); return u; } 35 else { t[v].ch[0]=merge(u,t[v].ch[0]),update(v); return v; } 36 } 37 void split_val(int now,int k,int& x,int& y) { 38 if(!now) return (void)(x=y=0); 39 if(t[now].val<=k) split_val(t[x=now].ch[1],k,t[now].ch[1],y); 40 else split_val(t[y=now].ch[0],k,x,t[now].ch[0]); 41 update(now); 42 } 43 void split_k(int now,int k,int& x,int& y) { 44 if(!now) return (void)(x=y=0); 45 if(t[t[now].ch[0]].siz>=k) split_k(t[y=now].ch[0],k,x,t[now].ch[0]); 46 else split_k(t[x=now].ch[1],k-t[t[now].ch[0]].siz-1,t[now].ch[1],y); 47 update(now); 48 } 49 void ins(int x) { int u,a,b; t[u=++cnt].key=Rand(),t[u].val=x,t[u].siz=1,split_val(root,x,a,b),root=merge(merge(a,u),b); } 50 void del(int x) { int a,b,c,d; split_val(root,x-1,a,b),split_k(b,1,c,d),t[c].clear(),root=merge(a,d); } 51 int get_rank(int x) { int a,b,c; split_val(root,x-1,a,b),c=t[a].siz+1,root=merge(a,b); return c; } 52 int get_val(int& now,int x) { int a,b,c,d,e; split_k(now,x-1,a,b),split_k(b,1,c,d),e=t[c].val,now=merge(a,merge(c,d)); return e; } 53 int pre(int x) { int a,b,c; split_val(root,x-1,a,b),c=get_val(a,t[a].siz),root=merge(a,b); return c; } 54 int sub(int x) { int a,b,c; split_val(root,x,a,b),c=get_val(b,1),root=merge(a,b); return c; } 55 int main() { 56 n=read(); int opt,x; 57 while(n--){ 58 opt=read(),x=read(); 59 switch(opt){ 60 case 1: ins(x); break; 61 case 2: del(x); break; 62 case 3: print(get_rank(x)); break; 63 case 4: print(get_val(root,x)); break; 64 case 5: print(pre(x)); break; 65 case 6: print(sub(x)); break; 66 } 67 } Ot(); return 0; 68 }
推荐题目
题目
洛谷 —— 列队
分析
首先我们分析一下这个列队的性质;
首先每次操作时,先让一个人 (a,b) 出队 。
然后右边的人跟上来,空缺的位置变成了 (a,m) (也就是在一棵平衡树中删除了一个节点)

最后其实也就是最后一列的跟到上面,空缺的位置变成 (n,m) ,然后出队的人到这个位置上
于是非常显然的,题目就是要你维护 n 棵平衡树,
但是看看数据范围:3e5 ... 于是发现这题不可做
那么我萌就要用到一个巧妙的思路—— 缩点与拆点 了。
什么意思? 你再看眼数据范围:3e5 ... 没毛病?
对啊,询问也是 3e5 啊... 所以说我们是不是维护了许多用都用不到的点呢?
于是我们把一大段区间的没用的点缩成一个点,让这个点记录区间左右信息就好了咯。
emmm...你说的没错,我们怎么知道哪些点该缩哪些点不该缩呢?
简单,我们点全都缩起来,要用的时候再拆出来不就好了?
然后还要注意的就是最后一列的特殊性,要单独维护(也就 3e5 个点嘛,开得下),
这点从图中应该也看得出来(何况这些点并不属于一个区间!)
于是愉快地上代码...
代码

1 //by Judge 2 #include<iostream> 3 #include<cstdio> 4 #define ll long long 5 #define int long long 6 using namespace std; 7 const int M=3e5+111; 8 #define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) // 手动输入需要去掉这句话 9 char buf[1<<21],*p1=buf,*p2=buf; 10 inline int read(){ 11 int x=0,f=1; char c=getchar(); 12 for(;!isdigit(c);c=getchar()) if(c=='-') f=-1; 13 for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x*f; 14 } 15 char sr[1<<21],z[20];int C=-1,Z; 16 inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;} 17 inline void print(int x){ 18 if(C>1<<20)Ot();if(x<0)sr[++C]=45,x=-x; 19 while(z[++Z]=x%10+48,x/=10); 20 while(sr[++C]=z[Z],--Z);sr[++C]=' '; 21 } 22 ll n,m,q,cnt,root,rt[M]; 23 struct Node { int key,ch[2]; ll l,r,siz; } t[M<<4]; 24 inline int Rand() { static int seed=703; return seed=(ll)(seed*48271LL%(~0u>>1)); } 25 inline int update(int now){ t[now].siz=t[t[now].ch[0]].siz+t[t[now].ch[1]].siz+t[now].r-t[now].l+1; } 26 inline int newnode(ll x,ll y) { int u=++cnt; t[u].l=x,t[u].r=y,t[u].siz=y-x+1,t[u].key=Rand(); return u; } 27 int merge(int u,int v) { 28 if(!u || !v) return u|v; 29 if(t[u].key<t[v].key) { t[u].ch[1]=merge(t[u].ch[1],v),update(u); return u; } 30 else { t[v].ch[0]=merge(u,t[v].ch[0]),update(v); return v; } 31 } 32 void split_new(ll now,ll k){ //把一个节点拆成两个节点 33 if(k>=t[now].r-t[now].l+1) return ; int nw=newnode(t[now].l+k,t[now].r); 34 t[now].r=t[now].l+k-1,t[now].ch[1]=merge(nw,t[now].ch[1]),update(now); 35 } 36 void split(int now,int k,int& x,int& y) { //常规操作 37 if(!now) return (void)(x=y=0); 38 if(t[t[now].ch[0]].siz>=k) split(t[y=now].ch[0],k,x,t[now].ch[0]); 39 else{ 40 split_new(now,k-t[t[now].ch[0]].siz),k-=t[t[now].ch[0]].siz, 41 split(t[x=now].ch[1],k-(t[now].r-t[now].l+1),t[now].ch[1],y); 42 } update(now); 43 } 44 signed main(){ 45 n=read(),m=read(),q=read(); 46 for(ll i=1;i<=n;++i) 47 rt[i]=newnode((i-1)*m+1,i*m-1); 48 for(ll i=1;i<=n;++i) 49 rt[n+1]=merge(rt[n+1],newnode(i*m,i*m)); 50 while(q--){ 51 ll a=read(),b=read(),x,y,z; 52 if(b^m){ 53 ll xx,yy,zz; split(rt[a],b,x,y), 54 split(x,b-1,x,z),print(t[z].l), 55 split(rt[n+1],a,xx,yy),split(xx,a-1,xx,zz); 56 rt[a]=merge(merge(x,y),zz),rt[n+1]=merge(merge(xx,yy),z); //拆完合并 57 } 58 else{ 59 split(rt[n+1],a,x,y),split(x,a-1,x,z); 60 print(t[z].l),rt[n+1]=merge(merge(x,y),z); 61 } 62 } Ot(); return 0; 63 }
最后感谢 axjcy 大佬的 blog
