【问题描述】
我们准备根据一份文本编码表对一篇文本进行压缩。编码表的每一项包含两个部分:要编码的字符串和对应的编码。编码是二进制的01串,用来替代文本中相应的字符串以实现压缩编码的目的。这些01串不一定是等长的。文本压缩所要考虑的问题是对给定的文本和编码表,求出能令整个文本的编码最短的二进制串的长度。例如文本:abcdef
编码表
a | abc | abcd |bcd|def|ef
01 | 0 | 1011 |1 |10 |11
下面有3种不同的方式进行编码:
方式1:长度为5
a bcd ef
01 1 11
方式2:长度为3
abc def
0 10
方式3:长度为6
abcd ef
1011 11
很明显,方式2长度最短,你的任务是找出编码后文本的最短长度,若不能进行编码,则输出0.
【输入格式】
输入可能包含多个文本压缩问题。
第一行是一个整数n,表示有n个文本压缩问题。(n≤10)
每个文本压缩问题的描述第一行是要压缩的文本(不超过210个字符),接下来是编码表,每项一行,不超过100项,只包含小写字母,外侧有小括号。
【输出格式】
对应每个文本压缩问题,每行输出一个最小长度。
【输入输出样例】
输入样例:
2
abcdef
(a,01)
(abc,0)
(abcd,1011)
(bcd,1)
(def,10)
(ef,11)
aa
(a,1)
(ab,10)
输出样例:
3
2
分割线君又来调皮了 _ (:з」∠)_
赛后和老师讨论了一下这道 t ,发现虽说是有点麻烦,但是也不是很坑[ 远没有t1坑 _ ( :з」∠) _ ] , 如果用字典树优化的话(其实不优化也能A过去,而且优不优化都是0ms,可以说数据水么?)可以降降时间复杂度,但是我又测了一下效率之后发现可能这么做丝毫没有优化时间复杂度(原因:原题目中的编码表项数太小+原数据太水),如果说编码表项数的上线是一万(1e4)的话那么用字典树做优化很明显…不然随随便便枚举编码表然后加个dp这道题也能水过去[PS: 测试点只有5个]
但是字典树貌似也有个缺陷就是要开较大的数组(这道题在数据水的情况下我轻松就能在字典树210个节点的情况下A了,还是数据水…),最最最最关键的就是要开多大的数组还很难算,本题数据贱的话貌似要2X1e4个节点的样子(最坏情况),如上所说如果说编码表项数是1万的话就是2X1e6的样子.(所以说这题数据真心水,210个节点也就这么划过去了)
然后这题我就A了20。。。TAT 所以第一个程序的源代码我就不放了 (还有一个原因就是我懒)_ (:з」∠)_
那么这道题既然说了字典树就用字典树讲吧,顺便让童鞋们(也和我一起)科普科普字典树这玩意儿。另外,本篇blog不会详细讲字典树的内容,所以请童鞋们自行百度。
然后我就先简要概括一下字典树这(辣鸡)玩意儿吧:
Trie树,又称字典树,单词查找树或者前缀树,是一种用于快速检索的多叉树结构,如英文字母
的字典树是一个26叉树,数字的字典树是一个10叉树。与二叉查找树不同,Trie树的键不是直接
保存对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有
叶子节点和部分内部节点所对应的键才有相关的值。
它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询
效率比哈希树高。
搜索字典项目的方法为:
1. 从根结点开始一次搜索;
2. 取得要查找关键词的第一个字母,并根据该字母选择对应的子树并转到该子树继续进行检索;
3. 在相应的子树上,取得要查找关键词的第二个字母,并进一步选择对应的子树进行检索。
4. 迭代过程……(我也搞不懂是神马玩意儿,反正在这里应该就是下标一类的玩意儿了)
5. 在某个结点处,关键词的所有字母已被取出,则读取附在该结点上的信息,即完成查找。
顺便盗个图
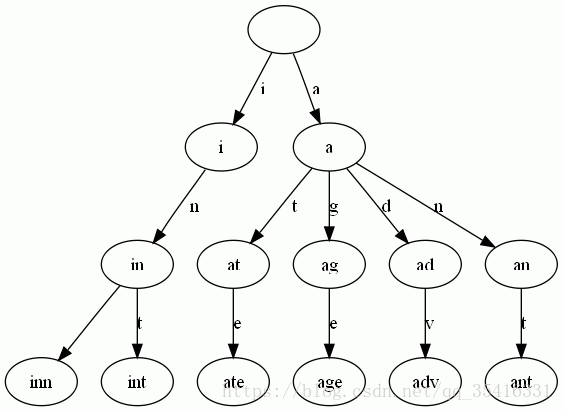
emm…都是借鉴来的介绍、、、其他关于字典树的东西这里就不赘述了,如有兴趣自行百度。
好了,上代码吧。(对了,程序里的主函数中有许多字符串的函数,如有不懂的可以去搜一下,顺便当做复习)
include<bits/stdc++.h> //运用字典树来处理查找问题
using namespace std;
int n,k,h,rt;
string s,p;
int len,v,dp[210]; //dp[i]表示在做到i号位置时付出的最小价值
int trie[210][26]; //trie[i][j]表示在第i号节点的后继中,有无j字母,
//如果有,那么这个后继的编号则记录在trie[i][j]中
int val[210]; //val[i]表示在字典树的第i号节点上有无完整字符串
//如果有,那么这个字符串的价值就记录在val[i]中
void work()
{
len=s.length(); //len赋值为s的(有效)长度
s=" "+s; //s前加个空格方便操作
for(int i=1;i<=len;++i) //从前往后做dp
{
rt=0; //从根节点开始查找
for(int j=i;j>=1;--j)
//一直往前找,按照要压缩的文本字符串查找是否已有此字符串编码
{
int x=s[j]-'a';
if(!trie[rt][x]) break; //查无此字符串,则直接退出
//(找不到当前节点的话后面也不用再找下去了,相当于树到这里已经断了,
//字符串在字典树中已经不可能匹配了)
rt=trie[rt][x]; //获得该节点的后继 x 字母的节点编号
if(val[rt]!=0x3f3f3f3f && dp[j-1]!=0x3f3f3f3f)
dp[i]=min(dp[i] , dp[j-1]+val[rt]); //取最小值
}
}
cout<< (dp[len]==0x3f3f3f3f ? 0 : dp[len]) <<endl; //直接输出dp[len]
}
int main()
{
ios::sync_with_stdio(false); //输入输出流的优化,你懂的 (o^.^o)
cin>>n>>s;
while(n--)
{
k=0; h=0;
memset(trie , 0 , sizeof(trie));
memset(val , 0x3f , sizeof(val));
memset(dp , 0x3f , sizeof(dp)); dp[0]=0; //将整个dp数组赋值inf之后,
//要把dp[0]赋为0,作为dp的基础
while(cin>>p && p[0]=='('){ //这里就是对读入的数据是否是编码表项
len=p.find(',')-p.find('(')-1; // 运用字符串函数得到p的长度 和 价值
v=p.find(')')-p.find(',')-1;
p=p.substr(1,len); //取出真正的 编码
rt=0;
for(int i=len-1;i>=0;--i)
//这里从后往前存点,因为等会儿的dp也是从后往前匹配的
{
int x=p[i]-'a'; //得到的x代表了26个字母之一
if(!trie[rt][x]) //如果尚未有点就自己建一个点
trie[rt][x]=++h;
rt=trie[rt][x]; //然后rt指向当前节点的后继 x 字母
}
val[rt]=min(val[rt] , v); //最终在树的字符串底端
}
work();
s=p; //之前读入的非编码表项其实是要压缩的文本,直接赋值给s
}
return 0;
}ok,这就是字典树的做法了。希望童鞋们看完后能有所收获 QAQ
另外附上我的实验结果(十组数据时):
| 编码表项数优化方法 | 无优化线性枚举 | 区间预处理 | 字典树优化 |
|---|---|---|---|
| 100 | 70ms | 40ms | 50ms |
| 1000 | 350ms | 90ms | 60ms |
| 10000 | 3200ms | 570ms | 240ms |
然后……再见 _ (:з」∠)_