才发现扫描线可以用树状数组搞... 致远星患者
(另外根据这篇博文的内容怎么越来越感觉自己往 PJ 入门靠拢了...)
还有一点,咱把树状数组当做线段树来康的话其实一切都会很清晰,这个来张四合一的图:
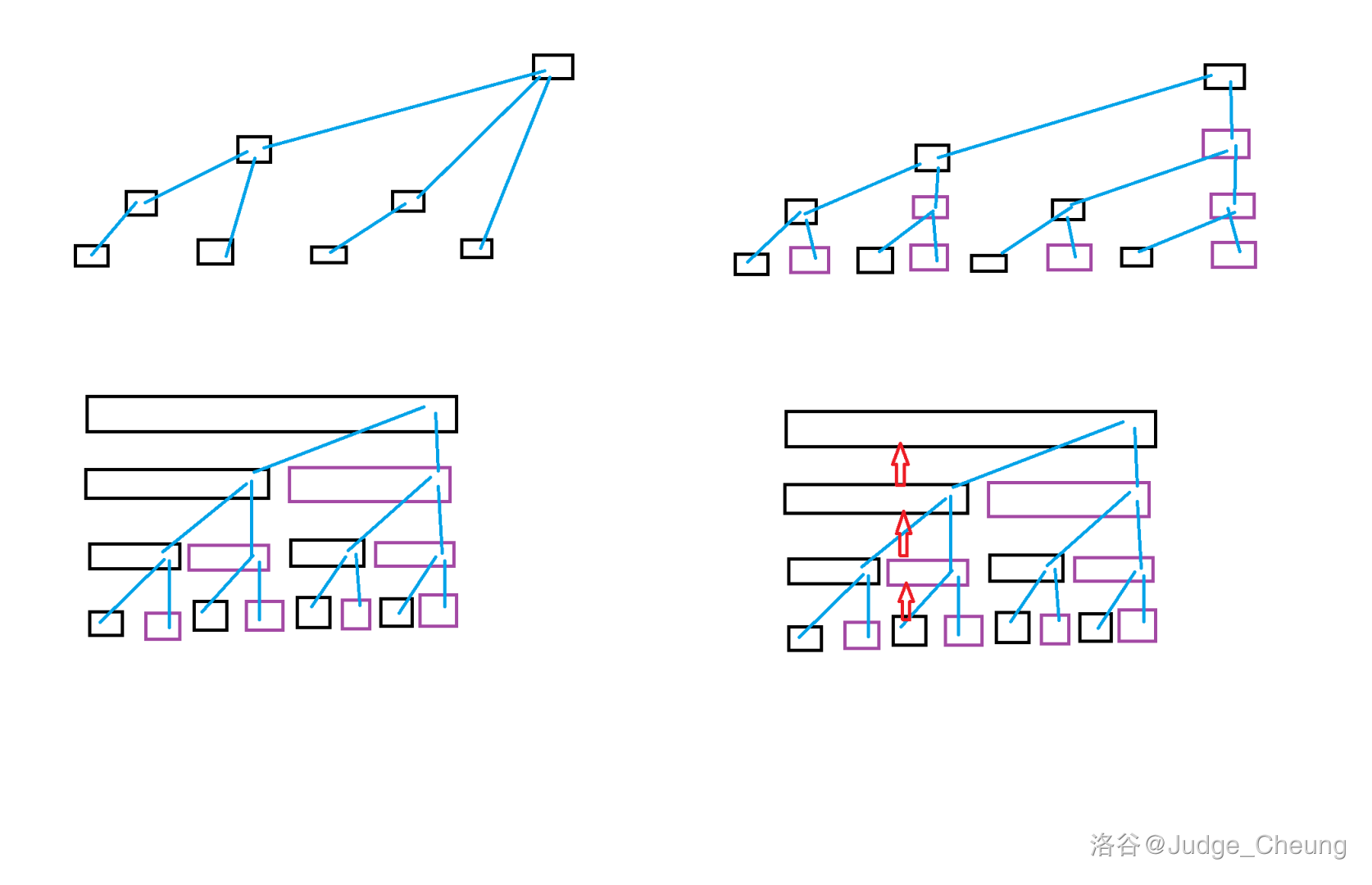
第一张就是随处可见的 sb 树状数组剖析图了
第二张咱把点补齐了一下,即每个点下面所有层都赋值一份点,然后以第一张图类似的规则连边,同时某个点正下方的点也要向其连边
第三张咱把点长补全了,看起来... 是不是很像线段树了呢? 2333
然后第四张图写了一下某个点 update 时的虚拟状况,某个点一直往上跑就好辣,至于 query 时,类比线段树查询 1~x 内的信息(也就是前缀信息嘛),把查询点对应到这里,不就变成了每次去掉一个 lowbit 嘛
这样,对于受众较少的 OI 龄较大但对于树状数组只是几个模板的(指自己) OIer 们来说,这篇博文的价值大部分就已经完成了...
那么还有一小部分就是树状数组(在理解了以上内容之后),在扫描线中的应用 ...
你可能已经在挠头了??? 线段树不是区间查询搞的扫描线?? 什么时候树状数组也能来凑热闹了?
脑补一下,拆成两个前缀和可不就是区间嘛, 但其实,树状数组不能艹扫描线 【雾 (就算能咱也不会啊 QwQ)
不过在这里,还有一个另一种情况的(伪)扫描线可以用树状数组优化二维前缀和来做
eg
询问 单个矩阵 与 多个矩形(互不相交,划重点) 的面积交之和 , 多组询问 ,资瓷离线 ,要求复杂度一只 log ,并且略略卡常(虽说原题时限给了 10 S 就是了)
数据比较友好,不需要离散... (讲道理可能 PJ 的同学倒能一眼看出二维前缀和,然后想着用 BIT 优化??? 虽说还是很超纲就是了)
Code
真 tm 好打,明明用线段树维护的话会是个码农题的说,用了树状数组多在纸上比划两下就好了
//by Judge
#include<bits/stdc++.h>
#define ll long long
#define Rg register
#define pb push_back
#define P pair<int,int>
#define fi first
#define se second
#define fp(i,a,b) for(Rg int i(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(Rg int i(a),I=(b)-1;i>I;--i)
#define go(u) for(Rg int i=head[u],v=e[i].to;i;v=e[i=e[i].nxt].to)
#define open(S) freopen(S".in","r",stdin),freopen(S".out","w",stdout)
using namespace std;
const int M=2e6+3;
typedef ll arr[M];
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
inline int read(){ int x=0,f=1; char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x*f;
} char sr[1<<21],z[20];int CCF=-1,Z;
inline void Ot(){fwrite(sr,1,CCF+1,stdout),CCF=-1;}
inline void print(ll x,char chr='
'){
if(CCF>1<<20)Ot();if(x<0)sr[++CCF]=45,x=-x;
while(z[++Z]=x%10+48,x/=10);
while(sr[++CCF]=z[Z],--Z);sr[++CCF]=chr;
} int n,m,W,L; ll ans[M]; vector<P> ql[M],qr[M],op[M];
namespace BIT {
arr f,fx,fy,fs;
#define lowbit(x) (x&-x)
inline void add(int x,int l,int r,ll s,int v) { ++x;
while(x<=L+1) f[x]+=v,fx[x]+=v*l,fy[x]+=v*r,fs[x]+=v*s,x+=lowbit(x);
}
inline ll ask(int x,int l,int r) { ll sx=0,sy=0,s=0,ct=0; ++x;
while(x) ct+=f[x],sx+=fx[x],sy+=fy[x],s+=fs[x],x^=lowbit(x);
return ct*l*r-l*sy-r*sx+s;
}
} using namespace BIT;
signed main() { open("intersec"); int a,b,c,d;
n=read(),m=read(),W=read(),L=read();
fp(i,1,n) a=read(),b=read(),c=read(),d=read(),
op[a].pb(P(b,1)),op[a].pb(P(d,-1)),op[c].pb(P(b,-1)),op[c].pb(P(d,1));
fp(i,1,m) a=read(),b=read(),c=read(),d=read(),
ql[a].pb(P(d,i)),qr[a].pb(P(b,i)),ql[c].pb(P(b,i)),qr[c].pb(P(d,i));
fp(i,0,W) {
for(auto x: qr[i]) ans[x.se]+=ask(x.fi,i,x.fi);
for(auto x: ql[i]) ans[x.se]-=ask(x.fi,i,x.fi);
for(auto x: op[i]) add(x.fi,i,x.fi,1ll*i*x.fi,x.se);
} fp(i,1,m) print(ans[i],"
"[i<m]); return Ot(),0;
}