HDU

同学们~ 

Stars

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 7966    Accepted Submission(s): 3181

Problem Description

Astronomers often examine star maps where stars are represented by points on a plane and each star has Cartesian coordinates. Let the level of a star be an amount of the stars that are not higher and not to the right of the given star. Astronomers want to know the distribution of the levels of the stars. 



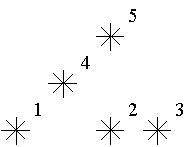For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it's formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3. 

You are to write a program that will count the amounts of the stars of each level on a given map.

 

Input

The first line of the input file contains a number of stars N (1<=N<=15000). The following N lines describe coordinates of stars (two integers X and Y per line separated by a space, 0<=X,Y<=32000). There can be only one star at one point of the plane. Stars are listed in ascending order of Y coordinate. Stars with equal Y coordinates are listed in ascending order of X coordinate.

 

Output

The output should contain N lines, one number per line. The first line contains amount of stars of the level 0, the second does amount of stars of the level 1 and so on, the last line contains amount of stars of the level N-1.

 

Sample Input

5 1 1 5 1 7 1 3 3 5 5

 

Sample Output

1 2 1 1 0

 

题意：给定N个星星的坐标，求每个星星坐下区域内的星星个数（xi <= x && yi <= yi）,不包括本身。一般方法肯定TEL，因此可以采用线段树或者树状数组进行优化查询。这里采用树状数组，具体原理可以参考下一篇博客，这里说题。

思路：题目是按照 y 值增加的顺序读入点坐标的，y相等时按x从小到大。因此我们想一下会发现，不用管y坐标，只用管x坐标。想一下在x坐标轴上，先读入的一层星星对应x轴上的N个点，后读入的y坐标肯定比先读入的大或者相等。因此肯定满足y的要求，我们只需统计该星星左边的星星有多少个即可。并加入该星星，向上更新到祖先结点。

代码：

#include <iostream>
#include <cstring>
using namespace std;

int c[32005];
int ans[15005];
int n;

int lowbit(int x){
    return x&(-x);
}
void add(int id,int p){
    while(id <= 32005){     //向上更新区间到最大值，注意不是 n
        //cout<<"check:  "<<id<<"  "<<lowbit(id)<<"  "<<c[id]<<endl;
        c[id] += p;
        id += lowbit(id);
    }
}
int sum(int id){
    int sum = 0;
    while(id >= 1){
        sum += c[id];
        //cout<<"check:  "<<id<<"  "<<lowbit(id)<<endl;
        id -= lowbit(id);
    }
    return sum;
}
int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    while(cin>>n){
        int x,y;
        memset(ans,0,sizeof(ans));
        memset(c,0,sizeof(c));
        for(int i = 1;i <= n;i ++){
            cin>>x>>y;

            int res = sum(x+1);
            ans[res]++;
            add(x+1,1);
        }
        for(int i = 0;i < n;i ++)
            cout<<ans[i]<<endl;
    }
    return 0;
}